17.11.1 Няхай у некаторым базісе рэчаіснай прасторы V лінейны аператар f мае матрыцу 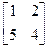 . Знайсці ўласныя вектары і ўласныя значэнні f.
. Знайсці ўласныя вектары і ўласныя значэнні f.
Рашэнне. Знойдзем характэрыстычны паліном аператара f:
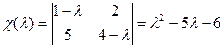
Яго корані 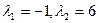 па тэарэме 17.10 з’яўляюцца ўласнымі значэннямі аператара f. Знойдзем, якім уласным вектарам яны адпавядаюць.
па тэарэме 17.10 з’яўляюцца ўласнымі значэннямі аператара f. Знойдзем, якім уласным вектарам яны адпавядаюць.
Калі 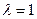 , вектару
, вектару 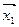 адпавядае слупок каардэнат
адпавядае слупок каардэнат 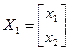 , тады X 1 – рашэнне сістэмы
, тады X 1 – рашэнне сістэмы 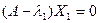 ;
; 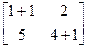
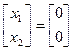 ;
; 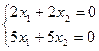 .
.
Фундаментальную сістэму рашэнняў утварае слупок 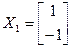 . Усе рашэнні гэтай сістэмы -
. Усе рашэнні гэтай сістэмы - 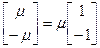 , што адпавядае 17.6 і 17.7.
, што адпавядае 17.6 і 17.7.
Адпаведна, 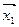 мае слупок каардэнат
мае слупок каардэнат 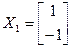 у базісе, аб якім ідзе гаворка ў задачы.
у базісе, аб якім ідзе гаворка ў задачы.
Калі 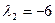 адпавядае уласнаму вектару
адпавядае уласнаму вектару 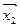 , які ў базісе з умовы мае слупок каардэнат
, які ў базісе з умовы мае слупок каардэнат 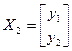 , тады, як і раней, атрымаем сістэму адносна y1, y2:
, тады, як і раней, атрымаем сістэму адносна y1, y2: 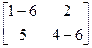
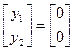 ;
;
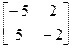
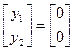 ;
; 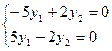
Такім чынам, атрымоўваем, што ўласным вектарам 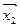 з’яўляецца вектар, які мае ў базісе, які разглядаем, слупок каардынат
з’яўляецца вектар, які мае ў базісе, які разглядаем, слупок каардынат 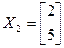 (ці адвольны ненулявы калініярны яму вектар).
(ці адвольны ненулявы калініярны яму вектар).
17.11.2 Няхай у некаторым базісе рэчаіснай прасторы V лінейны аператар f мае матрыцу 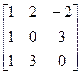 . Знайсці ўласныя значэнні аператара f і слупкі ўласных вектараў, якім гэтыя ўласныя значэнні адпавядаюць.
. Знайсці ўласныя значэнні аператара f і слупкі ўласных вектараў, якім гэтыя ўласныя значэнні адпавядаюць.
Знаходзім характэрыстычны паліном  аператара f:
аператара f:
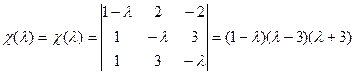 .
.
Такім чынам, уласныя значэнні роўныя 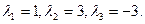 Знойдзем уласныя вектары, якім адпавядае ўласнае значэнне
Знойдзем уласныя вектары, якім адпавядае ўласнае значэнне 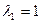 . Няхай ён мае слупок каардынат
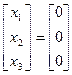
. Няхай ён мае слупок каардынат 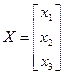 , тады
, тады 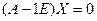 ;
; 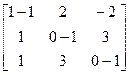
 ;
; 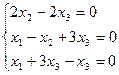 .
.
Рашэнне гэтай сістэмы дае нам, што 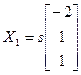 , дзе s≠0, так як
, дзе s≠0, так як 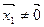 .
.
Аналагічна, уласнае значэнне 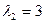 адпавядае ўласным вектарам, якія маюць слупкі
адпавядае ўласным вектарам, якія маюць слупкі 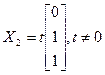 . Аналагічна, калі
. Аналагічна, калі 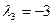 , тады
, тады 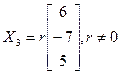 .
.
Прыклад 17.11.3. Няхай у некаторым базісе рэчаіснай лінейнай прасторы V лінейны аператар f мае матрыцу 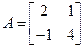 . Знайсці ўласныя вектары і ўласныя значэнні f.
. Знайсці ўласныя вектары і ўласныя значэнні f.
Характэрыстычны паліном f: 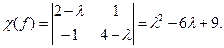
Уласнае значэнне 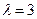 (кратнасці 2), якому адпавядае ўласны вектар
(кратнасці 2), якому адпавядае ўласны вектар 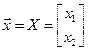 . Тады
. Тады 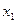 і
і 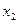 – рашэнні сістэмы
– рашэнні сістэмы 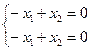 , значыць,
, значыць, 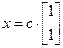 , дзе
, дзе 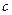 Î R \{0}.
Î R \{0}.
Прыклад 17.11.4. Няхай у некаторым базісе рэчаіснай лінейнай прасторы V лінейны аператар f мае матрыцу 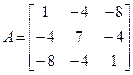 .Знайсці ўласныя вектары і ўласныя значэнні f.
.Знайсці ўласныя вектары і ўласныя значэнні f.
Характэрыстычны паліном f мае корані 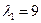 (кратнасці 2),
(кратнасці 2), 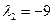 (кратнасці 1).
(кратнасці 1).
Калі ўласнае значэнне 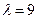 адпавядае ўласнаму вектару
адпавядае ўласнаму вектару
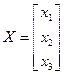 , тады
, тады 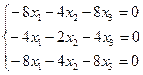 , што эквівалентна раўнанню
, што эквівалентна раўнанню 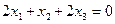 , адкуль вынікае, што ўласнае значэнне
, адкуль вынікае, што ўласнае значэнне 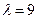 адпавядае ўласным вектарам
адпавядае ўласным вектарам 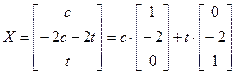 , дзе
, дзе 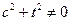 . Аналагічна знаходзім, што ўласнае значэнне
. Аналагічна знаходзім, што ўласнае значэнне 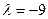 адпавядае ўласным вектарам
адпавядае ўласным вектарам 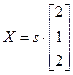 , дзе
, дзе 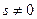 .
.
Прыклад 17.11.5. Няхай у некаторым базісерэчаіснайлінейнай прасторы V лінейны аператар f мае матрыцу 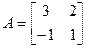 . Знайсці ўласныя вектары і ўласныя значэнні f.
. Знайсці ўласныя вектары і ўласныя значэнні f.
Характэрыстычны паліном 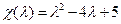 не мае рэчаісных каранёў, значыцца, аператар f не мае ўласных вектароў і ўласных значэнняў.
не мае рэчаісных каранёў, значыцца, аператар f не мае ўласных вектароў і ўласных значэнняў.
Прыклад 17.11.6. Няхай у некаторым базісе камплекснай лінейнай прасторы V лінейны аператар f мае матрыцу 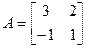 . Знайсці ўласныя вектары і ўласныя значэнні f.
. Знайсці ўласныя вектары і ўласныя значэнні f.
Характарыстычны паліном 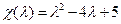 мае камплексныя корані
мае камплексныя корані 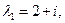
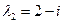 . Нескладана знайсці, што гэтыя ўласныя значэнні адпавядаюць уласным вектарам
. Нескладана знайсці, што гэтыя ўласныя значэнні адпавядаюць уласным вектарам 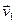 і
і 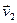 , якія ў дадзеным базісе маюць слупкі каардынат
, якія ў дадзеным базісе маюць слупкі каардынат 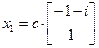 ,
, 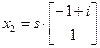 , дзе
, дзе 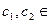 C
C 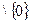 .
.
Ул-ць 17.12. Няхай dim V =n. Лінейны аператар f ÎEnd(V) мае ў некаторым базісе дыяганальную матрыцу тады і толькі тады, калі ўсе вектары гэтага базіса – ўласныя вектары f.
Доказ. Калі f у базісе 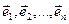 мае матрыцу
мае матрыцу 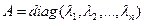 , тады з азначэння матрыцы аператара маем, што
, тады з азначэння матрыцы аператара маем, што 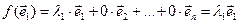 , і наогул,
, і наогул, 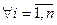 ,
, 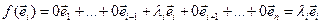 . Значыцца, вектары базіса
. Значыцца, вектары базіса 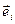 – уласныя вектары аператара f, якім адпавядаюць уласныя значэнні
– уласныя вектары аператара f, якім адпавядаюць уласныя значэнні 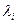 . Калі
. Калі 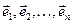 – базіс прасторы V, прычым
– базіс прасторы V, прычым 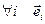 – уласныя вектары аператара f, якім адпавядаюць уласныя значэнні
– уласныя вектары аператара f, якім адпавядаюць уласныя значэнні 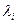 , тады
, тады 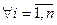
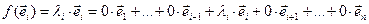 , адкуль, па азначэнню 11.2 атрымоўваем, што ў базісе
, адкуль, па азначэнню 11.2 атрымоўваем, што ў базісе 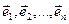
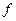 мае матрыцу
мае матрыцу 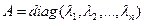 .■
.■
Ул-ць 17.13. Уласныя вектары лінейнага аператара, якія адпавядаюць папарна розным уласным значэнням, лінейна незалежныя.
Доказ. Выкарыстаем метад матэматычнай індукцыі па k – колькасці ўласных вектароў.
Калі k=1, уласцівасць, відавочна, праўдзівая (паколькі ўласны вектар – нянулявы).
Няхай сцвярджэнне праўдзівае да k вектароў 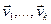 , якія адпавядаюць папарна розным уласным значэнням
, якія адпавядаюць папарна розным уласным значэнням 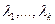 .
.
Разгледзім k+1 уласны вектар 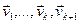 , якім адпавядаюць папарна розныя уласныя значэнні
, якім адпавядаюць папарна розныя уласныя значэнні 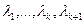 . Няхай
. Няхай 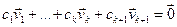 (6)
(6)
Тады 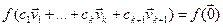 , значыцца
, значыцца 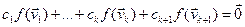 , адкуль
, адкуль 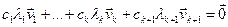 . (7)
. (7)
Калі абедзве часткі роўнасці (6) дамножым на 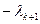 і дададзім да роўнасці (7), атрымаем, што
і дададзім да роўнасці (7), атрымаем, што 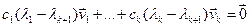 . Па пасылцы індукцыі вектары
. Па пасылцы індукцыі вектары 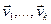 – лінейна незалежныя, значыцца,
– лінейна незалежныя, значыцца, 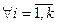
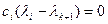 , а паколькі
, а паколькі 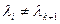 ,
, 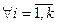
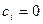 . З гэтага і роўнасці (6) вынікае, што
. З гэтага і роўнасці (6) вынікае, што 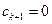 , значыцца, вектары
, значыцца, вектары 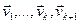 – лінейна незалежныя. ■
– лінейна незалежныя. ■
Вынік 17.14. Калі dim V =n і лінейны аператар f ÎEnd(V) мае n папарна розных уласных значэнняў 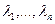 , тады ўласныя вектары, якім яны адпавядаюць, лінейна незалежныя, утвараюць базіс V, у якім f мае матрыцу
, тады ўласныя вектары, якім яны адпавядаюць, лінейна незалежныя, утвараюць базіс V, у якім f мае матрыцу 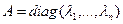 .
.
Доказ. З тэарэмы 17.10 вынікае, што калі 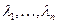 – розныя уласныя значэнні, яны адпавядаюць розным уласным вектарам
– розныя уласныя значэнні, яны адпавядаюць розным уласным вектарам 
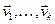 , якія па ўласцівасці 17.13 лінейна незалежныя, значыцца, утвараюць базіс прасторы V, у якім па ўласцівасці 17.1 2 лінейны аператар f мае матрыцу A =
, якія па ўласцівасці 17.13 лінейна незалежныя, значыцца, утвараюць базіс прасторы V, у якім па ўласцівасці 17.1 2 лінейны аператар f мае матрыцу A = 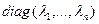 .■
.■
Вынік 17.15. Калі A ÎMat(n´n,P) і характэрыстычны паліном матрыцы A мае n розных каранёў 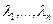 , тады існуе нявыраджаная матрыца T такая, што
, тады існуе нявыраджаная матрыца T такая, што 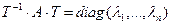 .
.
Доказ. Разгледзім якую-небудзь лінейную прастору V над P вымернасці n (напрыклад Pn) і фіксуем у ёй базіс 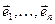 (3).
(3).
Згодна з 11.4, існуе лінейны аператар f, які ў гэтым базісе мае матрыцу A. Па 17.8 і 17. 9 характэрыстычныя паліномы f і A аднолькавыя, значыцца, f мае n папарна розных уласных значэнняў 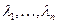 , значыцца, існуе базіс
, значыцца, існуе базіс 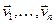 (8) прасторы V, у якім усе вектары – уласныя вектары аператара f, якім адпавядаюць розныя ўласныя значэнні
(8) прасторы V, у якім усе вектары – уласныя вектары аператара f, якім адпавядаюць розныя ўласныя значэнні 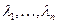 , значыцца, па 17.4, у базісе (8) f мае матрыцу
, значыцца, па 17.4, у базісе (8) f мае матрыцу 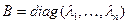 . Калі T – матрыца пераходу ад базіса (3) да базіса (8), тады па тэарэме 11.8,
. Калі T – матрыца пераходу ад базіса (3) да базіса (8), тады па тэарэме 11.8, 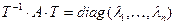 .■
.■
Прыклад 17.16. У гэтым прыкладзе матрыцы з 17.16.k будуць тыя ж, якія былі былі ў прыкладзе 17.11.k Паспрабуем адказаць на пытанне: Ці існуе да дадзенай матрыцы 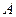 такая матрыца
такая матрыца 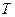 , што матрыца
, што матрыца 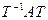 – дыяганальная?
– дыяганальная?
Прыклад 17.16.1. 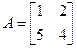
У 17.11.1 знайшлі ўласныя значэнні 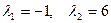 , якія адпавядаюць уласным вектарам
, якія адпавядаюць уласным вектарам 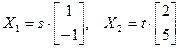 , дзе
, дзе 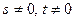 . Згодна з 17.15
. Згодна з 17.15 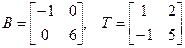 . Заўважым, што адказ мог выглядаць і інакш, напрыклад, калі ўзяць
. Заўважым, што адказ мог выглядаць і інакш, напрыклад, калі ўзяць 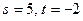 , атрымаем уласныя вектары
, атрымаем уласныя вектары 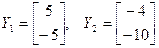 , адкуль, умове задачы задавальняе і матрыца
, адкуль, умове задачы задавальняе і матрыца 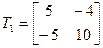 .
.
Наогул, да ўсіх матрыц 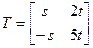 , дзе
, дзе 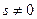 і
і 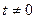 ,
, 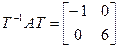 . Заўважым, што не толькі матрыца T знаходзіцца не адзіным чынам, але і матрыца B таксама, паколькі калі б мы абазначылі
. Заўважым, што не толькі матрыца T знаходзіцца не адзіным чынам, але і матрыца B таксама, паколькі калі б мы абазначылі 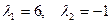 , тады атрымалі б, што
, тады атрымалі б, што 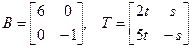 , дзе
, дзе 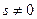 і
і 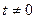 . Такім чынам, матрыца
. Такім чынам, матрыца 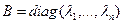 , калі яна існуе, азначана адзіным чынам з дакладнасцю да парадку элементаў на дыяганалі.
, калі яна існуе, азначана адзіным чынам з дакладнасцю да парадку элементаў на дыяганалі.
У наступных прыкладах мы будзем прыводзіць адзін з магчымых адказаў.
Прыклад 17.16.2. 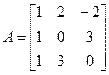 . Раней энайшлі тры розныя ўласныя значэнні
. Раней энайшлі тры розныя ўласныя значэнні 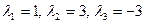 , якія адпавядаюць уласным вектарам са слупкамі каардынат
, якія адпавядаюць уласным вектарам са слупкамі каардынат 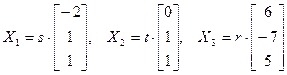 , дзе
, дзе 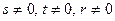 . Тады
. Тады 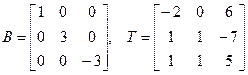 .
.
Прыклад 17.16.3. 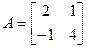 . Уласнае значэнне
. Уласнае значэнне 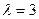 – адно. Усе уласныя вектары, якім яно адпавядае, калінеарныя, паколькі, яны маюць слупкі каардынат
– адно. Усе уласныя вектары, якім яно адпавядае, калінеарныя, паколькі, яны маюць слупкі каардынат 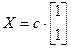 , cÎ R \{0}. Такім чынам, не існуе базіса V, які утвараюць уласныя вектары адпаведнага аператара f (глядзі доказ 17.15).
, cÎ R \{0}. Такім чынам, не існуе базіса V, які утвараюць уласныя вектары адпаведнага аператара f (глядзі доказ 17.15).
Значыцца, па 17.12, не існуе такой матрыцы T, каб матрыца 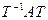 была дыяганальнаю.
была дыяганальнаю.
Прыклад 17.16.4. 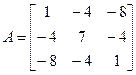
У гэтым выпадку, як і ў 17.16.3, існуе кратны корань 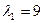 , які адпавядае ўласным вектарам са слупкамі каардынат
, які адпавядае ўласным вектарам са слупкамі каардынат 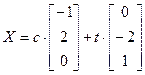 , дзе
, дзе 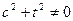 . Можам узяць два незалежных уласных вектара са слупкамі каардынат
. Можам узяць два незалежных уласных вектара са слупкамі каардынат 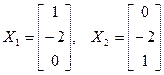 (нагадайце рашэнне аднародных сістэм лінейных раўнанняў і фундаментальныя сістэмы іх рашэнняў).Уласнае значэнне
(нагадайце рашэнне аднародных сістэм лінейных раўнанняў і фундаментальныя сістэмы іх рашэнняў).Уласнае значэнне 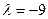 адпавядае уласнаму вектару са слупком каардынат
адпавядае уласнаму вектару са слупком каардынат 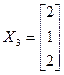 . З лінейнай незалежнасці першых 2-х вектароў і з 17.13 вынікае, што тры найдзеныя вектара ўтвараюць базіс прасторы, а тады па 17.12 атрымоўваем, што
. З лінейнай незалежнасці першых 2-х вектароў і з 17.13 вынікае, што тры найдзеныя вектара ўтвараюць базіс прасторы, а тады па 17.12 атрымоўваем, што 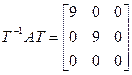 , дзе
, дзе 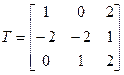 .
.
Прыклад 17.16.5 і 17.16.6. 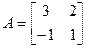 . З рашэння 17.11.5 і 17.11.6 вынікае, што для адвольнай нявыраджанай рэчаіснай матрыцы
. З рашэння 17.11.5 і 17.11.6 вынікае, што для адвольнай нявыраджанай рэчаіснай матрыцы 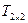 , матрыца
, матрыца 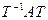 не будзе дыяганальнай (нагадайце 17.12).
не будзе дыяганальнай (нагадайце 17.12).
Але, калі разглядаць задачу над полем камплексных лікаў, тады, 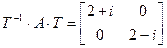 , дзе
, дзе 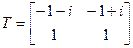 .
.
Заўважым, што ў прыкладах 17.16.3 і 17.16.4 пры наяўнасці кратных каранёў, атрымалі розныя адказы. Гэта тлумачыцца наступнаю тэарэмаю:
Тэарэма 17.17. Няхай A ÎMat(n´n,P) мае ўласныя значэнні 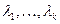 кратнасці
кратнасці 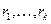 , тады існуе T ÎMat(n´n,P)такая, што
, тады існуе T ÎMat(n´n,P)такая, што 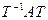 – дыяганальная ў тым і толькі ў тым выпадку, калі выконваюцца 2 умовы:
– дыяганальная ў тым і толькі ў тым выпадку, калі выконваюцца 2 умовы:
1) 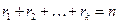
2) 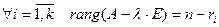 .
.
(Без доказу.) ■
 2015-07-14
2015-07-14 499
499








