Пусть функция 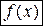 определена в некоторой окрестности точки
определена в некоторой окрестности точки 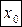 и имеет в этой точке производные до порядка
и имеет в этой точке производные до порядка 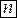 включительно. Тогда при
включительно. Тогда при 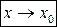 :
:
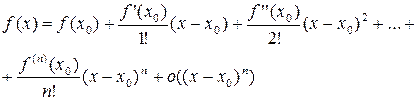
Эта формула называется формулой Тейлора порядка 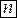 с остаточным членом в форме Пеано:
с остаточным членом в форме Пеано:
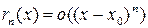
Если функция 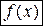 имеет в окрестности точки
имеет в окрестности точки 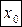 производную порядка
производную порядка 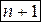 , то найдется такая точка
, то найдется такая точка 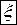 , лежащая между
, лежащая между 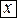 и
и 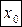 , что остаточный член формулы Тейлора можно записать в виде:
, что остаточный член формулы Тейлора можно записать в виде:
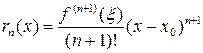 (форма Лагранжа)
(форма Лагранжа)
12. Формула Маклорена.
Формулой Маклорена называется формула Тейлора при 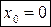 :
:
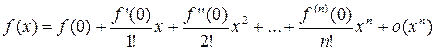 .
.
Остаточный член в форме Лагранжа записывается следующим образом:
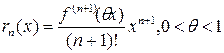
13. Разложение некоторых элементарных функций по формуле Тейлора.
1) 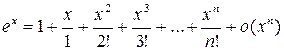 ;
;
2) 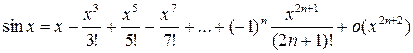 ;
;
3) 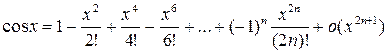 ;
;
4) 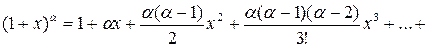
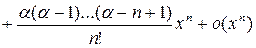 ;
;
5) 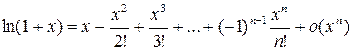 ;
;
14. Раскрытие неопределенностей. Правило Лопиталя.
Отыскание предела путем формальной подстановки значения точки, к которой стремится аргумент, в формулу, задающую рассматриваемую функцию, во многих случаях приводит к выражениям вида 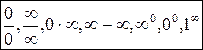 . Они называются неопределенностями, так как по ним нельзя судить, существует или нет указанный предел. В этом случае вычисление предела называется «раскрытием неопределенности».
. Они называются неопределенностями, так как по ним нельзя судить, существует или нет указанный предел. В этом случае вычисление предела называется «раскрытием неопределенности».
Теорема (правило Лопиталя для «раскрытия неопределенностей» вида  )
)
Пусть функции 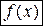 и
и 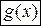 дифференцируемы в окрестности точки
дифференцируемы в окрестности точки 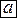 , существуют пределы
, существуют пределы 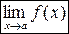 и
и 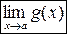 , равные 0 (для неопределенности вида
, равные 0 (для неопределенности вида 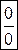 ) или
) или 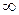 (для неопределенности вида
(для неопределенности вида 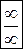 ), и
), и 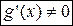 в окрестности точки
в окрестности точки 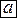 . Если существует предел
. Если существует предел 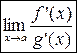 , то:
, то:
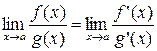 .
.
Иначе говоря, предел отношения функций в этом случае равен пределу отношения их производных.
15. Возрастание и убывание функций. Точки экстремума.
 2015-07-14
2015-07-14 225
225








