Покажем, что Rn(x) = o(x-a)n. Из выбора многочлена Pn(x) следует, что
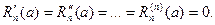 Применив для вычисления предела
Применив для вычисления предела
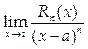
n раз правило Лопиталя, получим:

Утверждение доказано. Представление остаточного члена в виде Rn = o(x-a)n
называется записью остаточного члена в форме Пеано.
Найдем еще один вид записи Rn(x). Представим его в виде
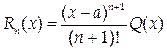
и определим вид функции Q(x). Из формулы Тейлора следует, что
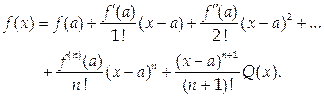
Пусть при заданных значениях х и а Q (x) =Q. Рассмотрим вспомогательную функцию от t (a < t < x):
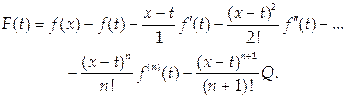
При этом предполагается, что а и х приняли фиксированные значения. Тогда
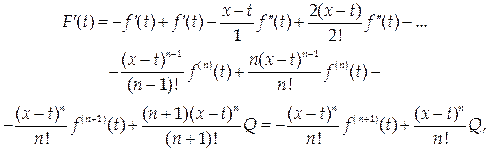
то есть F (t) дифференцируема в окрестности точки а. Из предыдущих выкладок следует, что F (x) = F (a) = 0, поэтому к функции F (t) можно применить теорему Ролля: существует t = x (a < x < x) такое, что F’ (x) = 0. Тогда
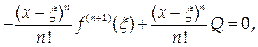
откуда Q = f ( n+ 1)(x). Используя это выражение, получим запись остаточного члена в форме Лагранжа:
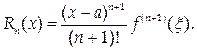
Так как a < x < x, можно представить x = а + q (х – а), где 0 < q < 1. При этом
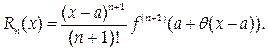
Замечание. Если в формуле Тейлора принять а = 0, этот частный случай называют формулой Маклорена:
|
|
|
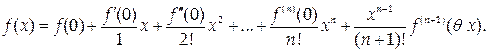
 2015-07-14
2015-07-14 290
290








