Центральная предельная теорема

Согласно центральной предельной теоремы закон распределения суммы достаточно большого числа независимых (или слабо зависимых) слагаемых, каждое из которых в отдельности мало влияет на сумму, сколь угодно близко к нормальному.

Опр. Случайной величиной 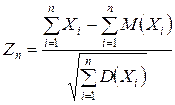называют нормированной суммой (центрированной случайной величиной)

Теорема 1. (Теорема Линдеберга - Леви)

Если 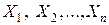– независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием m и дисперсией s², то при неограниченном увеличении n закон нормированной суммы Z_n сходится по вероятности к нормальному закону с плотностью вероятностей 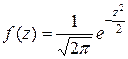(m = 0, s = 1). Без доказательства.

Замечание. В условиях теоремы при увеличении n закон распределения суммы 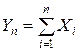также ненеограниченно приближается к нормальному (но с плотностью другого вида). Центральная предельная теорема справедлива и для неодинаково распределенных случайных величин.

Теорема 2. (теорема Ляпунова)

Если 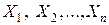– независимые случайные величины, имеющие математические ожидания m₁, …, m_n и дисперсии D₁, …, D_n причем

(*)

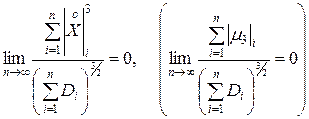где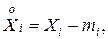

то при неограниченном увеличении n закон распределения нормированной суммы Z_n сходится по вероятности к нормальному закону. С плотностью вероятностей (без доказательства)

Другая формулировка: В условиях теоремы при n® ¥ закон распределения случайной величины 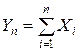неограниченно приближается к нормальному. Смысл условия (*) состоит в том, что действие " слагаемого невелико по сравнению с суммарным действием всех.

Практически центральной предельной теоремой можно пользоваться и в случае небольшого числа слагаемых (порядка 10): если суммируются случайные величины, сравнимые по своему рассеиванию.

Пример

1. Производится измерение некоторой величины a, суммарная ошибка измерения является случайной величиной, распределенной по нормальному закону (воздействует много факторов, порождающих малую ошибку X_i)