Задание 2. 1. Составить множество Еi и нарисовать диаграмму орграфа  i (V, Ei), где V = {0, 5, 7, 8, 10, 15}, а Ei - бинарное отношение, заданное на множестве V:
i (V, Ei), где V = {0, 5, 7, 8, 10, 15}, а Ei - бинарное отношение, заданное на множестве V:
а) Е 1= {(a, b) / a + b = 15; a, b Î V };
б) Е 2= {(a, b) / a < b; a, b Î V };
в) Е 3= {(a, b) / a ³ b; a, b Î V };
г) Е 4= {(a, b) / a × (b +1) = 0; a, b Î V }.
Подсказка. Изобразите все пять вершин, и подпишите их. В результате получим:
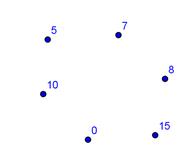
а) Выбираем две вершины, например 5 и 10, они будут соединены ребром, так 5+10=15, вершины 5 и 0, не соединены ребром, так как 5+0≠15.
Рассуждая, таким образом, построим граф  1(V, E 1):
1(V, E 1):
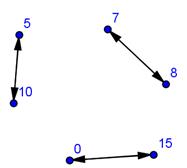
Двойные стрелочки указывают на то, что изображено два ребра в одну и другую сторону. Самостоятельно постройте остальные графы. Перенесите задание и диаграммы графов в тетрадь.
2. Изобразите полные ориентированные графы с шестью, пятью и четырьмя вершинами. Сколько ребер у полного орграфа с 4 (5 и 6) вершинами? Сколько ребер у полного орграфа с n вершинами?
Подсказка. Это можно сделать, например, так.
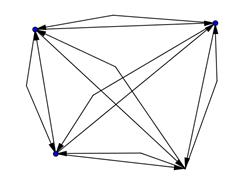
В полном ориентированном графе каждая вершина соединена со всеми остальными, не забудьте, что ребра считаются разными, если у них различная ориентация. Изображенный граф является регулярным орграфом степени 3.
|
|
|
3. Изобразите регулярный граф степени 2 и 3 с шестью вершинами. Сколько ребер у регулярного графа степени 2 (степени 3) в случае n вершин? Сколько ребер у регулярного графа степени k в случае n вершин?
Подсказка. Для неориентированного псевдографа Γ количество deg (v) рёбер, инцидентных вершине v ÎΓ, называется локальной степенью или просто степенью этой вершины.
Неориентированный граф называется однородным степени k (регулярным), если степени всех его вершин равны между собой и равны k.
4. Для графа, мультиграфа и 2-х псевдографов из занятия 1, задание 7 определите степени всех вершин и их сумму (выпишите в тетрадь диаграммы графа, мультиграфа и 2-х псевдографов, степени каждой вершины и сумму всех степеней вершин для каждого графа).
Подсказка. При изображении на диаграмме петли к этой вершине примыкают два конца петли, т.е. петля вносит в эту степень вклад 2.
5. Если возможно, изобразите кубический граф с 7 и 8 вершинами. Если данный граф не существует, то объясните почему.
Подсказка. Регулярный граф степени 3 называется кубическим.
6. Существует ли граф с 5 вершинами, степени которых различны между собой?
Подсказка. У такого графа степени должны быть равны 0, 1, 2, 3, 4.
7. Нарисуйте граф с 5 вершинами, у которого ровно 2 вершины имеют одинаковую степень.
Подсказка. Таких графов существует два.
8. Все вершины графа Γ(V, E)(| V | = n, | E | = m) имеют степень k или k +1. Доказать, что если Γ имеет nk вершин степени k и nk +1 вершин степени k +1, то nk = (k +1) n - 2 m.
|
|
|
Подсказка. Посчитайте сумму степеней всех вершин и приравняйте ее к удвоенному числу ребер. Выразите из полученного равенства nk.
9. Существуют ли графы со следующими степенями верши:
а) 2, 3, 4, 7, 7, 8, 6, 3, 0, 5;
б) 2, 1, 10, 7, 9, 8, 5, 4, 0, 7.
Доказать, что в любом графе количество вершин нечётной степени чётно.
Подсказка. Сумма степеней всех вершин графа - чётное число, равное удвоенному числу рёбер.
10. Если в графе с 5 вершинами ровно 2 вершины имеют одинаковую степень, то могут ли они обе быть изолированными или обе иметь степень 4?
Подсказка. Попробуйте изобразить оба случая.
11. В тренировочном турнире участвовало 12 команд, причём между каждыми двумя командами было сыграно по 3 матча. Сколько всего было проведено матчей?
Подсказка. Сколько ребер у регулярного графа степени3 в случае 12 вершин?
12. Доказать, что в любой компании, состоящей из 11 человек, найдутся 2 человека, имеющих одинаковое количество знакомых в этой компании.
Подсказка. Компанию рассматриваем как граф, люди – вершины, две вершины соединены ребром, если соответствующие люди знакомы.
Теорема. Во всяком графе с n вершинами, где n ³ 2, всегда найдутся, по меньшей мере, две вершины с одинаковыми степенями.
13. Во всякой ли компании найдутся 3 человека, у которых одинаковое количество знакомых в этой компании?
14. Девять шахматистов проводят турнир в один круг (каждый спортсмен должен сыграть с каждым из остальных по одному разу). Показать, что в любой момент времени найдутся двое, закончившие одинаковое число партий.
Подсказка. Каждому шахматисту поставим в соответствие вершину графа, а каждой сыгранной партии между двумя шахматистами - ребро, соединяющее вершины, соответствующие этим игрокам. В результате мы получим граф с девятью вершинами и некоторым неизвестным числом рёбер.
15. Дети в летнем лагере, познакомившись, обменялись конвертами с адресами. Доказать, что
а) всего было передано четное число конвертов;
б)число детей, обменявшихся конвертами нечетное число раз, четно.
Подсказка. Пусть дети - вершины графа, две вершины соединены ребром, если пара ребят, обменялась конвертами.
16. Изобразите регулярный орграф степени 2 и 3 с шестью вершинами. Сколько ребер у регулярного орграфа степени 2 (степени 3) в случае n вершин? Сколько ребер у регулярного орграфа степени k в случае n вершин?
Подсказка. Для вершин ориентированного графа определяются две локальные степени: r 1(v) - число рёбер с началом в вершине v (количество выходящих из v рёбер) и r 2(v) - количество заходящих в v рёбер (тех, для которых эта вершина является концом).
Ориентированный граф называется однородным степени k, если для каждой его вершины r 1(v)= r 2(v)= k.
Задание 3. 1.Постройте диаграммы орграфа 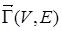 с семью вершинами и 13 ребрами.
с семью вершинами и 13 ребрами.
Подсказка. Вершины орграфа лучше изображать окружностями одинакового диаметра (для этого необходимо изобразить 7 точек, и на панели инструментов в вкладке Окружность по центру и точке  , выберите Окружность по центру и радиусу радиус можно выбрать равным 0.3(десятичная дробь задается через точку)), а ребра векторами. Например, можно изобразить этот граф так.
, выберите Окружность по центру и радиусу радиус можно выбрать равным 0.3(десятичная дробь задается через точку)), а ребра векторами. Например, можно изобразить этот граф так.
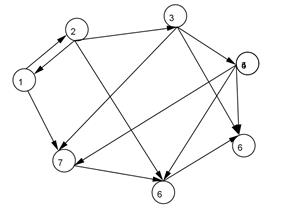
Подпишите вершины графа.
2. Орграф 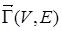 с семью вершинами и 13 ребрами преобразуйте в мультиорграф, для этого изобразите несколько кратных ребер. Подпишите ребра.
с семью вершинами и 13 ребрами преобразуйте в мультиорграф, для этого изобразите несколько кратных ребер. Подпишите ребра.
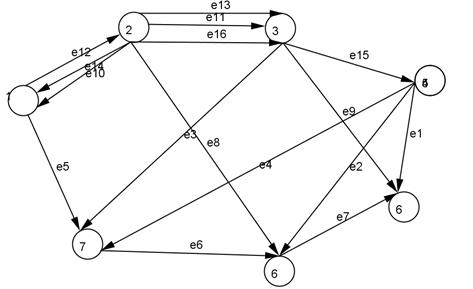
3. Орграф 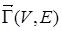 с семью вершинами и 13 ребрами преобразуйте в ориентированный псевдограф, для этого изобразите несколько петель (ребер у которых совпадает начало и конец).
с семью вершинами и 13 ребрами преобразуйте в ориентированный псевдограф, для этого изобразите несколько петель (ребер у которых совпадает начало и конец).
4. Мультиорграф 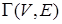 с семью вершинами и 16 ребрами преобразуйте в ориентированный псевдограф, для этого изобразите несколько петель.
с семью вершинами и 16 ребрами преобразуйте в ориентированный псевдограф, для этого изобразите несколько петель.
5. Для орграфа, мультиорграфа и 2-х ориентированных псевдографов из задание 3 определите две степени всех вершин и сумму для каждой степени (выпишите в тетрадь диаграммы орграфа, мультиорграфа и 2-х ориентированных псевдографов, две степени каждой вершины и сумму для каждой степени для каждого графа).
|
|
|
Подсказка. Петля даёт вклад 1 в обе эти степени. Очевидно, что общее количество всех выходящих рёбер равно общему количеству всех входящих рёбер и равно количеству рёбер этого графа: m = 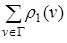 =
= 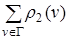 .
.
9. Существуют ли орграф со следующими степенями r 1 вершин:
а) 2, 3, 4, 7, 7, 8, 6, 3, 0, 5;
б) 2, 1, 10, 7, 9, 8, 5, 4, 0, 7.
 2015-08-12
2015-08-12 2565
2565







