1) To collect math`s literatures, and learn them.
2) To look through scientific literature and to do conclusion.]
Innovation of investigation:
Student has learned scientific literatures and compared the ways of innovation, and has made systematic decision.
Individual stage of investigation:
Student has shown the way of guessing fuction and has known the ways of guessing extremum points of function.
Conclusion of the work:
Comparing investigation ways of cub function and their structures, was shown possible.
The result of the work:
We can use this work in our out lesson works. This work shows the different guessing ways cub function.
Функция ұғымы тарихынан
Функциялық идеяның математика ғылымында да, мектепте математика пәнін оқытуда да пайда болған уақытын дәл айту қиын. Дегенмен ертедегі гректерде функциялық тәуелділік жайында кейбір жеке ұғымдар болған, ол орта ғасырларда қайтадан жойылып кеткен. Ал функциялық тәуелділікті графиктік кескіндеуді ХІІV ғасырдағы ғалымдардың еңбектерінде кездестіруге болады. Графиктердің функциялық мәнін қарастырмай-ақ еспті графиктік жолмен шешу мәселесі математиканың ертеректе шыққан әдебиеттерінде кездеседі.
XVI ғасырда Виет (1540-1603) әріп таңбаларды енгізген. Әріп арқылы түрлі шамаларды ұғынатын болғандықтан, айнымалы шама жайындағы түсінік те пайда болған.
Өзара тәуелді екі айнымалы шаманың өзгеруін көрнекті түрде кескіндеу француз математигі Р.Декарттың (1596-1650) есімімен байланысты. Ол өзінің «Геометрия» деп аталатын еңбегінде 1637 жылы тік бұрышты координаталар методын тұжырымдап берген.
«Функция» деген сөз деген латын сөзінен шыққан. Бұл сөздің қазақ тіліндегі мазмұны «әрекет», «атқару» деген сөздерге тән. Бұл сөз алғаш рет немістің атақты математигі Лейбництің (1646-1716 еңбектерінде кездеседі.
Лейбниц еңбектерінде «функция» деген сөз көрнекті-геометриялық түсінікте белгілі бір заңмен өзгеріп отыратын кесінді ретінде кездеседі.
Бір көңіл аударатын нәрсе – алғаш кезде функцияның аналитикалық формасы ескерілмей, оны тек графиктік түрде өрнектеген болатын. Тек XVIІ ғасырда ғана функцияның геометриялық формасынан оның аналитикалық формасына көшкен. Бұл кезең И.Бернуллидің есімімен байланысты. Ол «айнымалы шаманың функциясы сол айнымалы шама мен сандардан немесе тұрақты шамалардан белгілі әдіспен құрастырылған аналитикалық өрнек болып табылады» деп анықтай түседі.
1837 жылы француз математигі Л.Дирихле (1805-1859) функцияны былайша анықтаған: «Егер х-тің а 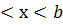 кесіндідегі кез келген мәніне у-тің әбден анықталған мәні сәйкес келсе, онда у айнымалы х-тің функциясы болып табылады (бұл сәйкестік қандай тәсілмен тағайындалған болса да бәрәбәр)».
кесіндідегі кез келген мәніне у-тің әбден анықталған мәні сәйкес келсе, онда у айнымалы х-тің функциясы болып табылады (бұл сәйкестік қандай тәсілмен тағайындалған болса да бәрәбәр)».
Карл Маркс өзінің «О понятии функции» деген еңбегінде функция жайындағы түсініктің элементер алгебраға ену тарихының негізгі түбірін анықтаған. Онда мынадай мысал кездеседі: «Қосындысы 10-ға тең екі бүтін оң санды табыңдар». Маркс х+у  10 теңдеуін құрып, іздеген сандардың бірінші белгісіздің орнына 1-ден 9-ға дейінгі сандарды қойып, мәндерді табуға болатындығын айтқан. Көптеген мысалдарды қарастыру соңында Маркс мынадай қорытындыға келген: «Сонымен, анықталмаған теңдеуден шыққан функцияның түсінігі былай еді:бір шамаға белгілі мән бермейінше екінші шаманы анықтауға болмайтындығының тәуелділігін белгілеу үшін функция деген сөзді пайдаланған.
10 теңдеуін құрып, іздеген сандардың бірінші белгісіздің орнына 1-ден 9-ға дейінгі сандарды қойып, мәндерді табуға болатындығын айтқан. Көптеген мысалдарды қарастыру соңында Маркс мынадай қорытындыға келген: «Сонымен, анықталмаған теңдеуден шыққан функцияның түсінігі былай еді:бір шамаға белгілі мән бермейінше екінші шаманы анықтауға болмайтындығының тәуелділігін белгілеу үшін функция деген сөзді пайдаланған.
Функцияның белгілі анықтамасын келтірейік. «Белгілі бір «Х» жиында берілген (немесе анықталған) функция деп, кейбір «Х» жиынның кез келген «Х» элементі сәйкес белгілі бір f(х) объектіні анықтайтын сәйкестікті айтады». Мұндай анықтама себептің салдар байланысы негізінде құрылған анықтамаға қарағанда неғұрлым дәл және неғұрлым жалпы болып табылады. Бұл келтірілген анықтама ортақ сипатта объектілердің арасында байланыс бар екендігін көрсетеді. Арасында сәйкестік тағайындалған жиындардың элементтері сан да, әріп те, геометриялық объекті де, нәрселер де т.б. да болуы мүмкін.
Қатынас, функция (бейнелеу), түрлендіру
Кез келген парлар жиыны қатынас деп аталады. Парлардың бірінші элементтер жиыны қатынастың анықтау облысы деп, ал екінші элементтер жиыны оның мәндер облысы деп аталады. Егер қатынастың анықталу облысы Х жиынының бөлігі, ал мәндер облысы Ү жиынының бөлігі болса, ондай қатынас Х және Ү жиындары элементтерінің арасындағы қатынас деп аталады. Х 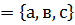 және Ү
және Ү 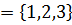 жиындарының арасындағы f,g,h,p қатынастар суретте бейнеленіп көрсетілген. Бірінші элементтері өзара тең емес парлардан тұратын қатынас функция деп аталады.
жиындарының арасындағы f,g,h,p қатынастар суретте бейнеленіп көрсетілген. Бірінші элементтері өзара тең емес парлардан тұратын қатынас функция деп аталады.
Мысалы, f, g, h қатынастары функция болып табылады, ал p қатынасы
функция бола алмайды, өйткені оған бірінші элементтері бірдей (в,1) және (в,2) екі пар еніп отыр. Егер х элементі у элементімен берілген қатынас түрінде байланысса, онда у элементі х элементіне сәйкес келеді дейді. Демек, функция дегеніміз анықталу облысының әрбір элементіне мәндер облысының бір ғана элементі сәйкес келетін қатынас болады. Жеке жағдайда f, g, h қатынастары үшін Х жиынының әрбір элементіне Ү жиынының бір ғана элементі сәйкес келмейді (яғни, әрбір х-ке (х Ү) Ү-тің біреуден артық емес элементі сәйкес келеді). Енді функцияның жоғарыда айтылғанмен мәндес тағы бір анықтамасын тұжырымдайық.
Функция деп кез келген х элементіне, бірінші элементі осы х болатындай, біреуден артық емес (-х,у) пары сәйкес келетін (х,у) парларының f жиынын атайды. Егер жиынының функция десек, онда (х,у) 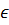 f сөйлемін у
f сөйлемін у 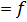 (х) арқылы жазады да у-ті функциясының аргумент х мәніне сәйкес мәні деп атайды. F функциясының анықталу облысы деп f жиынына енетін парлардың барлық бірінші элементтерінің жиыны деп атайды да, Д (f) арқылы белгілейді. F функчиясының мәнінің облысы деп f жиынына енетін парлардың барлық екінші элементтерінің жиынын атайды да Е (f) арқылы белгілейді.
(х) арқылы жазады да у-ті функциясының аргумент х мәніне сәйкес мәні деп атайды. F функциясының анықталу облысы деп f жиынына енетін парлардың барлық бірінші элементтерінің жиыны деп атайды да, Д (f) арқылы белгілейді. F функчиясының мәнінің облысы деп f жиынына енетін парлардың барлық екінші элементтерінің жиынын атайды да Е (f) арқылы белгілейді.
Д (f)және Е (f) жиындары Х және Ү жиындарының сәйкес бөліктері дейік.Енді «бейнелеу» термині «функция» терминінің синонимі болатынын мына мысалдар арқылы көрсетейік.
1. Егер Д (f)  Х, Е (f)
Х, Е (f)  Ү болса, онда f дегеніміз Х-ті Ү- ке бейнелеу болады.
Ү болса, онда f дегеніміз Х-ті Ү- ке бейнелеу болады.
2. Егер Е (f)  Х, Е (f)
Х, Е (f)  Ү болса, онда f дегеніміз Х-ті Ү- тің ішіне бейнелеу болады да, былай белгіленеді f
Ү болса, онда f дегеніміз Х-ті Ү- тің ішіне бейнелеу болады да, былай белгіленеді f 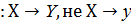
3. Егер Д (f)  Х, Е (f)
Х, Е (f)  Ү болса, онда f дегеніміз Х-тің белгілі бір бөлігін Ү- ке бейнелеу болады.
Ү болса, онда f дегеніміз Х-тің белгілі бір бөлігін Ү- ке бейнелеу болады.
4. Егер Д (f)  Х, Е (f)
Х, Е (f)  Ү болса, онда f дегеніміз Х-тің белгілі бір бөлігін Ү- тің ішіне бейнелеу болады.
Ү болса, онда f дегеніміз Х-тің белгілі бір бөлігін Ү- тің ішіне бейнелеу болады.
Сонымен бірге, Х 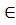 Д (f)
Д (f)  элементіне сәйкес келетін у
элементіне сәйкес келетін у 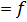 (х) элементі
(х) элементі 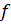 бейнеленуінде х элементінің бейнесі деп аталады.Ал барлық жиынын
бейнеленуінде х элементінің бейнесі деп аталады.Ал барлық жиынын
х 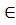 Х (f (х)
Х (f (х) 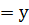 ) элементтерінің жиынын, у
) элементтерінің жиынын, у 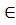 Е (f) элементінің толық алғашқы бейнесі деп атайды.
Е (f) элементінің толық алғашқы бейнесі деп атайды.
Егер әрбір у 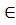 Е (f) үшін у
Е (f) үшін у 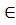 f (х) шартын қанағаттандыратын бір ғана
f (х) шартын қанағаттандыратын бір ғана
х 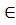 Е (f) элементі табылса, онда f функциясы деп аталады f бейнеленуі де қайтымды делінеді). Қайтымды f функциясының кері функциясы болады және былай жазылады:
Е (f) элементі табылса, онда f функциясы деп аталады f бейнеленуі де қайтымды делінеді). Қайтымды f функциясының кері функциясы болады және былай жазылады:
f (х) 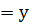
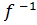 (у)
(у)  х
х
У-ке қайтымды бейнеленуі Х-тің У-ке өзара бір мәнді бейнеленуі деп аталады.Х-тің У-ке өзара бір мәнді бейнеленуі Х-ті түрлендіру деп аталады.
Функцияның берілу тәсілдері.
1. Функцияның парларды атау (кесте) арқылы берілуі.Бірінші элементтері анықталу облысын, ал екінші элементтері мәндер облысын құрайтын парлар жиынымен функцияның толық анықталатынын біз бұрыннан білеміз.Егер функцияның анықталу облысы арқылы жиын болса, мұндай функцияны барлық парларды атап көрсету арқылы беруге болады, яғни сол парлар жиынын мына кесте түрінде жазамыз:
Сонда х айнымалысының мәндері f функциясының анқталу облысын құрайды да, ал у мәндері функция мәндері облысын құрайды.Сандық функция үшін 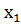 ,
, 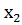 ,
, 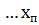 және
және 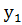 ,
, 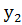 ,
, 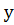 нақты сандар болады.Жалпы алғанда, кесте функцияны толық сипаттайды деуге болады.
нақты сандар болады.Жалпы алғанда, кесте функцияны толық сипаттайды деуге болады.
Шынында да, функция толық берілу үшін оның кейбір мәндерін ғана емес, барлық парлар жиынын білу керек болады.Алайда іс жүзінде функция мәндерінің кестесін тәжірибеге сүйеніп қана құрып жүреміз.Өзіміз білетін сандар квадраттарының, кубтарының,түбірлерінің, логарифмдерінің кестелері, сондай-ақ, тригонометриялық функциялар т.б. мәндер таблицаларының
(кестелерінің) әрқайсысы функциялар мәндерінің кестесі болып табылады.
2. Функцияның аналитикалық тәсілмен берілуі.Математикалық талдауда формула түрінде жазылған екі айнымалы өрнекпен сандық функцияның берілуі аса жиі кездеседі.Бұны функцияның аналитикалық тәсілмен берілуі деп атайды.Бұлайша берілу тәсілі анықталу облысы ақысыз жиын болып келген функцияларды сипаттап көрсетуге аса қолайлы.
Егер f функциясы у 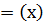 формуласымен беріліп, бірақ анықталу облысы аналитикалық у
формуласымен беріліп, бірақ анықталу облысы аналитикалық у 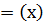 анықталу облысымен дәл келеді деп түсініледі.Мысалы, х
анықталу облысымен дәл келеді деп түсініледі.Мысалы, х 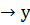 функциясы у
функциясы у 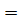
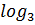 (х-2) формуласымен берілсін (анықталу облысы көсетілмеген) дейік.Сонда х
(х-2) формуласымен берілсін (анықталу облысы көсетілмеген) дейік.Сонда х 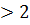 шартын қанағаттандыратын х мәндері жиыны (
шартын қанағаттандыратын х мәндері жиыны (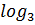 (х-2) өрнегінің анықталу облысы), яғни (2; +
(х-2) өрнегінің анықталу облысы), яғни (2; + 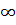 ) интервалы бұл функциясының анықталу облысы болып табылады.
) интервалы бұл функциясының анықталу облысы болып табылады.
3. Функцияның графиг арқылы берілуі. Сандық жиындар арасындағы қатынасты (тәуелділікті) көрнекті түрде, оның графигін пайдалана отырып көрсетуге болады. Ол үшін жазықтықты барлық (х,у) нүктелерін салу жеткілікті, сонда (х,у) парларының бірінші элементтері абциссалар да, ал екіншілері – ординаталар. Егер де график бойында абциссалары бірдей нүктелер болмаса, яғни әрбір абциссаға тек бір ғана ордината сәйкес келетін болса, онда осы графикпен анықталған қатынас функция болады.
Функциялардың қарапайым сипаттамалары
Анықталу облысы мен мәндер облысы нақты сандар R жиынының бөліктері болатын функциялар сандық функциялар деп аталады. Енді осы сандық функцияның анықтамасын келтірейік. Сандық функция деп, кез келген х санына бірінші элементі осы х болатындай, біреуден артық емес (х,у) пары сәйкес келетін (х,у) парларының f жиынын атайды. Осы аталған бір ғана пардағы екінші санды f (х) арқылы белгілейді. f функциясы (х, f (х)) парлары жиынының берілуімен толық анықталады, мұндағы D(f) жиынының барлық мәнін х қабылдайды да, ал Е(f) жиынының барлық мәнін f (х) қабылдайды. Егер біз «бейнелеу» терминін қолдансақ, онда f сан функциясы R жиынының қандай болса да бір D бөлігін, осы R жиынының басқа бір Е бөлігіне бейнеленетінін көреміз, Сонда D жиыны – функцияның анықталу облысы да, ал Е жиыны – оның мәндер лблысы. Қалыптасқан дәстүр бойынша х тәуелсіз айнымалы немесе аргумент деп, ал у тәуелдә айнымалы немесе функция деп аталады. Дұрысында функцияны у демей, жоғарыда келтірілген қасиетке ие болатын (х,у) парлардың f жиыны деу жөн. Сандық функциялардың кластарға бөлінуі. Сандық функцияларды аналитикалық өрнектері мен қасиеттеріне қарай екі класқа бөлуге болады. Бұл жолы біз аналитикалық өрнектеріне қарай функциялардың қалай бөлінетінін қарастырамыз. f функциясы у – D (х) формуласымен берілсін. Енді f (х) өрнегі үшін әр түрлі жағдайларды қарастырайық.
1) f (х) 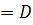 (х) өрнегін алу үшін х аргументі мен тұрақты сандарға саны шектеулі алгебралық амалдар (қосу, алу, көбейту, бөлу, түбір табу) қолданылатын болса, онда өрнекті алгебралық өрнек деп атайды.Алгебралық өрнектердің анықталу облысы мына шарттармен шектеледі:тек теріс емес сандардан ғана жұп көрсеткішті түбір табуға болады, нөлге бөлуге болмайды. Әрбір алгебралық f (х) өрнегі алгебралық делінетін у
(х) өрнегін алу үшін х аргументі мен тұрақты сандарға саны шектеулі алгебралық амалдар (қосу, алу, көбейту, бөлу, түбір табу) қолданылатын болса, онда өрнекті алгебралық өрнек деп атайды.Алгебралық өрнектердің анықталу облысы мына шарттармен шектеледі:тек теріс емес сандардан ғана жұп көрсеткішті түбір табуға болады, нөлге бөлуге болмайды. Әрбір алгебралық f (х) өрнегі алгебралық делінетін у  f (х) формуласымен берілген f яункциясымен байланысты. Алнебралық өрнектің анықталу облысы бос жиын болуы мүмкін. Әрине ондай өрнек бос функцияны анықтайды. Алайда, біз бос функцияны қарастырамыз.
f (х) формуласымен берілген f яункциясымен байланысты. Алнебралық өрнектің анықталу облысы бос жиын болуы мүмкін. Әрине ондай өрнек бос функцияны анықтайды. Алайда, біз бос функцияны қарастырамыз.
2) Алгебралық f (х) өрнегін құр үшін түбір табу амалы қолданылмаса, оны рационал өрнек деп атайды да, оған сәйкес функцияны рационал функция дейді.
3) Рационал f (х) өрнегін құру үшін бөлу амалы қолданылмаса, оны бүтін рационал өрнек деп атайды да, оған сәйкес функцияны бүтін рационал функция дейді. Бүтін рационал өрнекті көпмүше деп те атайды. Мұндай функциялардың мысалы ретінде сызықтық у 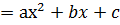 т.б. функциялардың қарастыруға болады.
т.б. функциялардың қарастыруға болады.
Алгебралық емес функцияларды трансценденттік функция деп атайды. Математиканың мектеп курсынан белгілі көрсеткіштік, логарифмдік, тригонометриялық, кері тригонометриялық функциялардың барлығы да трансценденттік функциялар қатарына жатады. Сондай-ақ, ху 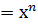 формуласымен (мұндағы а-иррационал сан) анықталатын функция да трансценденттік функция болады.
формуласымен (мұндағы а-иррационал сан) анықталатын функция да трансценденттік функция болады.
Сандық функциялардың өздеріне тән қасиеттеріне қарай сипаттамаларын қарастырайық.
а) Шенделген және шеңделмеген функциялар. Егер Х 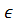 D (f) жиынында анықталған f функциясының сәйкес мәндерінің У жиыны шенделген болса, онда ол функция Х жиынында шенделген деп аталады.
D (f) жиынында анықталған f функциясының сәйкес мәндерінің У жиыны шенделген болса, онда ол функция Х жиынында шенделген деп аталады.
Жеке жағдайда, D(f) облысында шенделген f функциясы үшін оның мәндер облысы Е(f) шенделген жиын болады. Енді шенделген жиынның бұрын айтылған анықтамасын пайдаланып шенделген функция үшін алдыңғымен пара-пар бір анықтаманы келтірейік: егер оң с саны табылып, барлық х 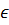 Х мәндері үшін f (х)
Х мәндері үшін f (х) 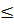 с теңсіздігі орындалса, онда f функциясы Х
с теңсіздігі орындалса, онда f функциясы Х 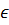 D(f) жиынында шенделген функция деп аталады.
D(f) жиынында шенделген функция деп аталады.
Жұп және тақ функциялар. Егер Х жиынында әрбәр х санымен бірге оған қарама-қарсы – х саны енетін болса, онда Х жиыны координаталар бас нүктесіне қатысты симметриялы жиын деп аталады. Анықталу облысы координаталар бас нүктесіне қатысты симметриялы Х жиыны болатын f функциясы үшін, егер кез келген х с Х мәніне сәйкес f (-х) 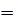 - f (х) теңдігі орындалса, онда оны жұп функция деп атайды. Анықталу облысы координаталар бас нүктесіне қатысты симметриялы Х жиыны болып табылатын f функциясы үшін, егер f (-х) тен - f (х) болса, онда оны тақ функция деп атайды. Егер де функцияның анықталу облысы D(f) координаталдар бас нүктесіне қатысты симметриялы жиын болмаса, онда функция жұп та, тақ та болмайды.
- f (х) теңдігі орындалса, онда оны жұп функция деп атайды. Анықталу облысы координаталар бас нүктесіне қатысты симметриялы Х жиыны болып табылатын f функциясы үшін, егер f (-х) тен - f (х) болса, онда оны тақ функция деп атайды. Егер де функцияның анықталу облысы D(f) координаталдар бас нүктесіне қатысты симметриялы жиын болмаса, онда функция жұп та, тақ та болмайды.
Мысалы: 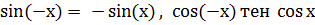 болғандықтан, бүкіл сандық түзуде
болғандықтан, бүкіл сандық түзуде 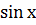 тақ функцияда,
тақ функцияда, 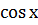 жұп функция болып табылады. f (х) тен
жұп функция болып табылады. f (х) тен 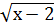 түбірі х
түбірі х 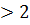 үшін, яғни координаталар бас нүктесіне қатысты симметриялы емес аралықта анықталған. Сондықтан сәйкес f функциясы тақ та, жұп та емес. Функцияның тақ болуы және жұп болу қасиеттерін оның графигін салғанда пайдаланады. Жұп функцияның графигі ордината осіне қатысты симметриялы да, ал тақ функцияның графигі координаталар бас нүктесіне қатысты симметриялы болып келеді.
үшін, яғни координаталар бас нүктесіне қатысты симметриялы емес аралықта анықталған. Сондықтан сәйкес f функциясы тақ та, жұп та емес. Функцияның тақ болуы және жұп болу қасиеттерін оның графигін салғанда пайдаланады. Жұп функцияның графигі ордината осіне қатысты симметриялы да, ал тақ функцияның графигі координаталар бас нүктесіне қатысты симметриялы болып келеді.
Периодты функциялар. Егер Х жиынына әрбір х пен бірге х-1 және х+1 мәндері де енетін болса, онда Х жиыны периодты І-ге тең периодты жиын деп аталады. Периодты жиынға мысал ретінде 2 жиынын (периоды І-ге тең) және Н жиынын(периоды кез келген сан) келтіруге болады. Ғ функциясы периоды l -ге тең периодты функция болу үшін:
1. D(f) тен Х жиыны периоды l –ге тең периодты жиын болуы тиіс.
2. Кез келген х с Х үшін f (х+ l)тен f (х) теңдігі орындалуы тиіс. Сонда f (х- l) тен f (х- l+l) тен f (х) теңдігінен, сондай-ақ, - l де f функциясының периоды болатынын байқаймыз.
О(нөл) саны кез келген функцияның периоды болып табылады. Алайда ондай периодты біз қарастырмаймыз. Егер f функциясының нөлден өзгеше периоды бар болса, онда оның оң санға тең периоды сөзсіз бар. f функциясының барлық оң периодтарының ең кішісі, осы функцияның негізгі периоды немесе периоды деп аталады. Сонымен, f функцияның ең кіші оң периоды бар болса, оны сол функцияның периоды деп атайды. Функцияның периодты болу қасиетін оның графигін салғанда пайдалану тиімді. Егер f функциясының периоды l болса, оның графигін салу үшін 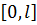 аралығындағы функция графигін білу жеткілікті, енді осы салынған графикті абциссалар осі бойымен кл аралығына көшіру керек.
аралығындағы функция графигін білу жеткілікті, енді осы салынған графикті абциссалар осі бойымен кл аралығына көшіру керек.
Бірсазды (монотонды) функциялар. Егер Е жиынына енетін кез келген 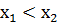 үшін f(
үшін f( 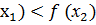 теңсіздігі орындалса, онда f функциясы Е жиынында өспелі функция деп аталады. Егер Е жиынына енетін кез келген
теңсіздігі орындалса, онда f функциясы Е жиынында өспелі функция деп аталады. Егер Е жиынына енетін кез келген 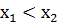 үшін f(
үшін f( 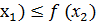 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда 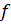 функциясы Е жиынында кемімейтін функция деп аталады. Егер Е жиынына енетін кез келген
функциясы Е жиынында кемімейтін функция деп аталады. Егер Е жиынына енетін кез келген 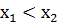 үшін f(
үшін f( 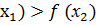 болса, онда f функциясы Е жиынында өспейтін функция деп аталады. Е жиынында өспелі, кемімейтін, кемімелі және өспейтін функцияларды осы жиында бірсазды функция деп атайды. Кейде өспелі және кемімелі функцияларды қатаң бірсазды деп те атайды.
болса, онда f функциясы Е жиынында өспейтін функция деп аталады. Е жиынында өспелі, кемімейтін, кемімелі және өспейтін функцияларды осы жиында бірсазды функция деп атайды. Кейде өспелі және кемімелі функцияларды қатаң бірсазды деп те атайды.
Негізгі элементар функциялар деп тұрақты функция және дәрежелік функцияны атайды.
Тұрақты функцияны бірінші элементі х кез келген нақты сан болатын, ал екінші элементі тұрақты С санына тең (х;С) парлар жиыны деп анықтауға болады. Әдетте оны у  С немесе f (х)
С немесе f (х) 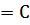 формулаларымен береді. Бұл функцияның анықталу облысы R жиыны, ал өзгеру облысы тек бір ғана тұрақты С санынан тұрады. Тік бұрышты координаталар жүйесінде у
формулаларымен береді. Бұл функцияның анықталу облысы R жиыны, ал өзгеру облысы тек бір ғана тұрақты С санынан тұрады. Тік бұрышты координаталар жүйесінде у  С мәндер облысы барлық нақты сандар жиыны, ал жұп болғанда теріс емес нақты сандар жиыны. Ал, n теріс сан болғанда бұл функция сандық осьтің х тен О нүктесінен өзге барлық нақты сандар жиыны болады да, ал n жұп сан болғанда, функцияның мәндер облысы тек нақты оң сандар.
С мәндер облысы барлық нақты сандар жиыны, ал жұп болғанда теріс емес нақты сандар жиыны. Ал, n теріс сан болғанда бұл функция сандық осьтің х тен О нүктесінен өзге барлық нақты сандар жиыны болады да, ал n жұп сан болғанда, функцияның мәндер облысы тек нақты оң сандар.
Кубтық функция және оны туындының көмегінсіз зерттеу
Кубтық функцияның максимум және минимум нүктелерін табу әдістерімен танысамыз.
Кубтық функцияның нүктелерін табу алдында нақты есептермен жалпы көріністерін қараймыз.
Мысал 1. f (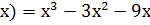 функциясын зерттеңдер және оның графигін салыңдар.
функциясын зерттеңдер және оның графигін салыңдар.
1. D (f)  R, онда f –көпмүшесі
R, онда f –көпмүшесі
2. f (-х) 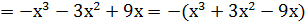
f (х) 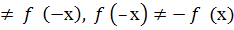 сондықтан, f функциясы тақ та, жұп та емес.
сондықтан, f функциясы тақ та, жұп та емес.
3. Графиктің нүктелерінің абцисса осін қиып өтетін нүктені табу үшін мына теңдеуді шешу керек.
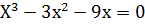
Х(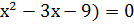
Х 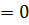
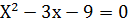
х 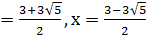
4. Функцияның таңба тұрақтылық аралықтарын анықтаймын.
- + - +
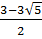 0
0 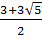 х
х
1-сурет
3 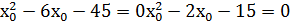
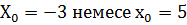
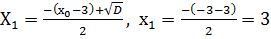
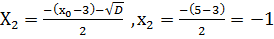
Сай келетін функциялардың мәндері
У(3) 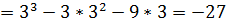
У(-1) 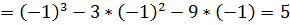
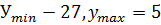
Зерттеліп отырған функцияның анықталған қасиеттерін есптеп, оның графигін көрсетеміз.
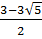
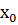
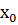
-2 -1 0 1 3 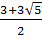 х
х
-27
3-сурет
Мысал 2.
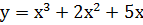 функциясының максимум және минимум (егер олар болса)нүктелерін табыңдар.
функциясының максимум және минимум (егер олар болса)нүктелерін табыңдар.
1) D(у) 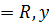 – көпмүше
– көпмүше
2) А(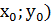 нүктесі функцияның граяигінде жатады. Абцисса осьіне параллель түзудің теңдеуі А(
нүктесі функцияның граяигінде жатады. Абцисса осьіне параллель түзудің теңдеуі А(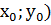 нүктесі арқылы өтеді. Абцисса мен түзудің графикпен қиылысатын нүктелерін анықтаймын.
нүктесі арқылы өтеді. Абцисса мен түзудің графикпен қиылысатын нүктелерін анықтаймын.
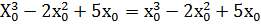
(х- 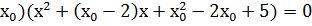
Х 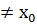
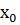 нүктесінен басқа нүктені іздейміз.
нүктесінен басқа нүктені іздейміз.
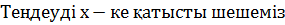 :
:
D 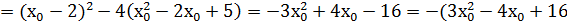 )
)
Х қандай да болмасын, D 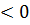 . Сондықтан А
. Сондықтан А 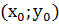 нүктесінен басқа
нүктесінен басқа
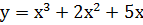 функция графигі у
функция графигі у 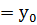 түзуімен басқадай екі қиылысу нүктесі жоқ. D(у)-қа қатысты функция монотонды.
түзуімен басқадай екі қиылысу нүктесі жоқ. D(у)-қа қатысты функция монотонды.
Онда жалпы жағдайға тоқталамын.
А 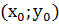 у
у 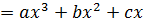 кубтық функциясына жатады, онда a
кубтық функциясына жатады, онда a 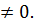
А 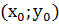 нүкте арқылы абцисса осіне параллель түзу жүргіземін. Салынған
нүкте арқылы абцисса осіне параллель түзу жүргіземін. Салынған
у 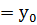 теңдеуінен, онда у
теңдеуінен, онда у 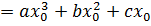 іздеймін.
іздеймін.
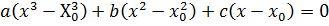
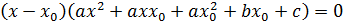
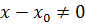 ,
,
А 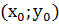 өзгеше абцисса нүктелерін іздеймін.
өзгеше абцисса нүктелерін іздеймін.
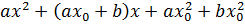 +c
+c 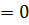
Х-ке қатысты квадраттық теңдеу аламын. Сондықтан, мен үш жағдайдан біреуін аламын.
1) Түзу функция графигін тағы да екі нүктеде қияды.
2) Түзу мен графиктің ортақ бір нүктесі болады.(жанасады).
3) А 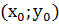 нүктесінен басқа түзу мен графиктің ортақ нүктесі болмайды.
нүктесінен басқа түзу мен графиктің ортақ нүктесі болмайды.
Кубтық функцияны графигі (4-сурет)а немесе б көріністері болуы мүмкін деп дұрыс есептеймін.
А 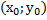 А
А 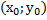 I
I
А 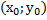 II
II
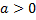 x
x
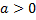
a) б)
А (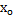 ;
; 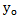 ) А (
) А (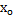 ;
; 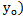 І
І
А (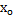 ;
; 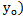 ІІ
ІІ
а 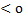 х а
х а 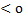 х
х
Кубтық функцияның экстремум нүктелерінің барлығын анықтау үшін алдағы зерттеуде а,б және с коэффициенттерінің кубтық функцияның формуласына ара қатынасын табу керек.
1) у 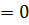 түзуінің кубтың функция графигімен абсциссадағы тағын екі ортақ нүктесін табамын.
түзуінің кубтың функция графигімен абсциссадағы тағын екі ортақ нүктесін табамын. 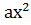 + (а
+ (а 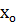 +b) х + а
+b) х + а 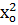 + b
+ b 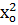 +с
+с  о теңдеуінде екі бөлек нақты түбірі болуы керек.Сондықтан теңдеудің дискриминанты оң сан боуы керек.
о теңдеуінде екі бөлек нақты түбірі болуы керек.Сондықтан теңдеудің дискриминанты оң сан боуы керек.
D 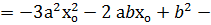 4 а с
4 а с
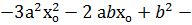 4 а с
4 а с 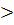 о
о
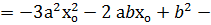 4 а с
4 а с 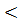 о
о
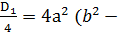 3 а с)
3 а с)
Егерде 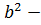 3 а с
3 а с 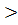 о онда
о онда 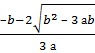
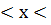
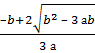
Егерде 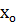 абсциссасы А нүктесінде осы интервал мәнін қабылдаса, онда у
абсциссасы А нүктесінде осы интервал мәнін қабылдаса, онда у 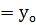 түзуі. А нүктесінен өтіп функциясының графигі тағы да екі нүктеде абсциссасына қияды.
түзуі. А нүктесінен өтіп функциясының графигі тағы да екі нүктеде абсциссасына қияды.
Егерде 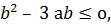 онда
онда 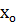 бірде бір мәні табылмайды.
бірде бір мәні табылмайды.
а 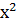 +(а
+(а 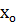 +
+ 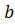 ) х + а
) х + а 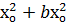 + с
+ с 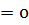
Теңдеу дискриминанты оң сан болу үшін.
2) Кубтың функциясымен у 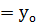 түзуінің абсиссадағытағы бір ортақ нүктесін табамыз.Теңдеуде екі бірдей нақты түбірі болуы керек.Сондықтан
түзуінің абсиссадағытағы бір ортақ нүктесін табамыз.Теңдеуде екі бірдей нақты түбірі болуы керек.Сондықтан
а 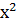 +(а
+(а 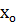 +
+ 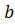 ) х + а
) х + а 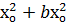 + с
+ с 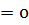
Теңдеудің Д дискриминанты о-ге теу болуы керек.
D 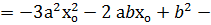 4 а с
4 а с
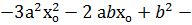 4 а с
4 а с  о
о
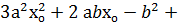 4 а с
4 а с  о (1)
о (1)
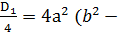 3 а с)
3 а с)
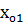
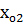 х
х
Егерде 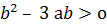 , онда теңдеудің екі әр түрлі нақты шешімін табамыз (1)
, онда теңдеудің екі әр түрлі нақты шешімін табамыз (1)
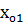

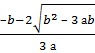 немесе
немесе 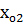

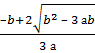
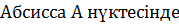 мына мәнді қабылдаса
мына мәнді қабылдаса
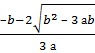 немесе
немесе 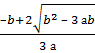
Онда А нүктесінен өтетін у 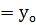 түзуі кубтық функция графигін тағы да бір нүктеде абсциссамен кеседі.
түзуі кубтық функция графигін тағы да бір нүктеде абсциссамен кеседі.
х 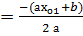 және х
және х 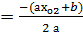
Табылған абсцисса нүктелері
х 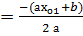 және х
және х 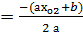 , онда
, онда
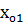

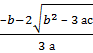 ,
, 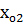

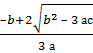
кубтық функцияның экстремум нүктелері болады.
Егерде 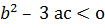 , онда теңдеуде (1) нақты түбір болмайды және Д
, онда теңдеуде (1) нақты түбір болмайды және Д 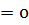
талабы орындалмайды.
Егерде 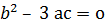 , онда теңдеуде (1) екі бірдей түбір болады:
, онда теңдеуде (1) екі бірдей түбір болады: 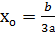
а 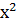 +(а
+(а 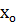 +
+ 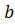 ) х + а
) х + а 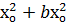 + с
+ с 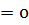 теңдеуде шешім болады.
теңдеуде шешім болады.
х 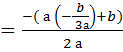
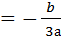
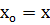 алдық, бірақ біздің зерттеуіміздің шарты бойынша біз А(
алдық, бірақ біздің зерттеуіміздің шарты бойынша біз А(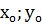 ) нүктелерін өзгеше абсцисса нүктелерін іздейміз.
) нүктелерін өзгеше абсцисса нүктелерін іздейміз.
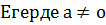
А) у 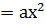
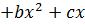 +d кубтық функция монотонды болады,
+d кубтық функция монотонды болады, 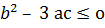
шарты орындалатын болса.
Б) Егерде 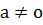 , у
, у 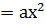
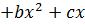 +d болса, онда функцияның экстренум нүктесі болады, егерде
+d болса, онда функцияның экстренум нүктесі болады, егерде 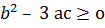 шарты орындалатын болса.
шарты орындалатын болса.
В) Егерде у 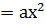
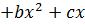 +d кубтық функцияда
+d кубтық функцияда 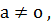
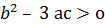
шарты орындалса, онда функция экстремумның екі нүктесі болады.
Г) кубтық функцияның графигі төменгі түрде болады (6- сурет)
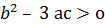
а 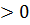 х а
х а 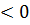 х
х
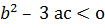
а 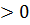 х а
х а 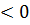 х
х
6- сурет
Д) у 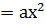
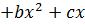 мәнінде
мәнінде 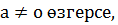 d тұрақты a санына. Сондықтан
d тұрақты a санына. Сондықтан
у 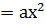
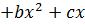 +d функция графигін құру үшін у
+d функция графигін құру үшін у 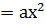
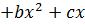 функциясының графигін ОУ осі бойымен d бірлігіне жылжытса жеткілікті.
функциясының графигін ОУ осі бойымен d бірлігіне жылжытса жеткілікті.
Функцияны туындының көмегімен зерттеу
Функцияның туынды көмегімен зерттеу алгоритмі арқылы функцияның
экстремум нүктелерін табуды және графигін салуды көрсетелік.
у 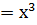
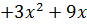
1. Д(у) 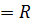
2. У(-х) 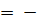
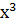
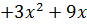 функция тақ та емес, жұп та емес.
функция тақ та емес, жұп та емес.
3. Функция графигінің координаталар осьтерімен қиылысу нүктесін табайық:
ОУ осі: х 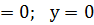 ; (0;0)
; (0;0)
ОХ осі: 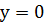 ;
; 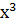
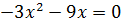
Х(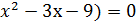
Х 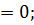
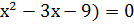
D 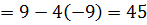
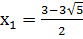 ;
; 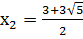 ;
;
(0;0), (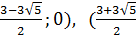 ;0).
;0).
4. Функцияның таңба тұрақтылық аралығын анықтау үшін анықталу облысын х 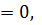 х
х 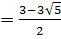 , х
, х 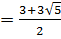 нүктелері арқылы интервалдарға бөліп, функцияның таңбасын анықтаймыз.
нүктелері арқылы интервалдарға бөліп, функцияның таңбасын анықтаймыз.
Сонда,
Х 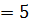 у(5)
у(5) 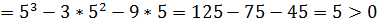
Х 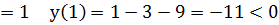
Х 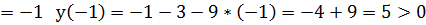
Х 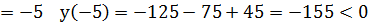
Енді интервалдарда анықталған функцияның таңбасын сан түзуіне қарастырамыз.
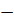 +
+ 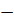 +
+
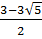 0
0 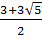
Демек, (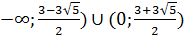 интервалында f(x)
интервалында f(x) 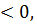 ал
ал
(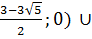 (
(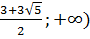 интервалында f(x)
интервалында f(x) 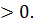
5. 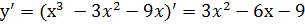 ;
;
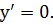
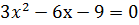 немесе
немесе 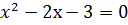
Онда 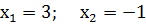
Анықталу облысын Х айнымалысының мәндерін қолданып, аралықтарға бөлеміз, әр аралықтағы туындының таңбасын интервалдар ісімен анықтаймыз.
Сонда х 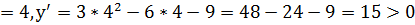 яғни (3;+
яғни (3;+ 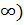 аралығында
аралығында 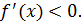
Интервалдарға функцияның туындысының таңбасын сан түзуіне кезекпен қоямыз
+ 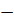 +
+
-1 -3
Демек, (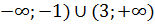 аралығында өседі, Өйткені
аралығында өседі, Өйткені 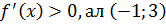
аралығында кемиді, өйткені 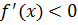 .
.
х 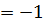 максимум нүктесі, х
максимум нүктесі, х 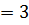 минимум нүктесі.
минимум нүктесі.
Экстремум нүктелеріндегі функцияның мәндерін есептейік:
у 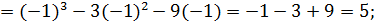 (-1;5)
(-1;5)
у 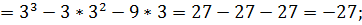 (3;-27).
(3;-27).
у 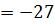
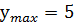 7
7
y
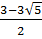 3
3
-1 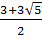 х
х
-27
Қорытынды
Ғылымның негізгі салаларының одан әрі дамып жетілуі математика пәнінен толық, тиянақты білім алу мәселесін өмір талабы ретінде бірінші кезекке қоюда.
Ақпараттық компьютерлік техрологияның кеңінен қолданылуы, әрбір адамның математикадан берік және түпкілікті игерілген білімнің болуын талап етеді.
Математикадағы басты ұғымдардың бірі – функцияның да өмірде алатын орны ерекше.
Осыған байланысты функция ұғымының даму тарихын білу, олардың берілу тәсілдерін, оларды зерттеудің әртүрлі тәсілдерін яғни интерпретациялардың түсіне алу, осы тәсілдерде есептер шығарып үйренудің маңызы зор және әрбір адамның математикалық білімінің кеңеюіне алып келеді.
Жұмыста осы мәселелер қарастырылып, зерттеу нәтижелері келтірілген жұмыс функция жайлы толық түсінік алуға, Функцияның экстремум нүктелерін туындының көмегінсіз табудың жолдарын түсіне білуге мүмкіндік береді.
Пайдаланылған әдебиеттер
1. Ш.Г.Омашев. Мектепте функциялық тәуелділікті оқыту жайында
Алматы. «Мектеп», 1986ж.3-5беттер
2. Қ.Қабдықайыр. Жоғары математика. 227-236 беттер.
3. Н.Я.Виленкии. Функции в природе и технике
Москва. Просвещение, 1978г. 128 стр
4. Ш.Бекбаулиева, Қ.И.Қаңлбаев, Н.Н.Забежанская, М.Б. Меңдіғалиева.
Алгебра және анализге кіріспе.
Алматы. «Ана тілі» 1991 ж. 46-47 беттер
5. Н.Я.Виленкин, А.М.Пышкало, В.Б.Рожденстренская, Л.П.Стойлова.
Математика. Москва. Просвещение, 1978 г. 162 стр
6. Э.Васильева, С.Забелина. Кубическая функция.
Москва. «Математика» 2003 г. 15 стр.
7. З.А.Гусев, А.Г.Мордкович. Математика.
Москва. «Просвещение», 1990 г. 84-86 стр.
8. Н.Я.Виленкин, О.С.Ивашев-мусатаев, С.И.Шварцбурд.
Алгебра и математикический анализ.
М:Мнемозина, 2003 г. 57-58 стр.
9. Ә.Н.Шыныбеков. Алгебра және анализ бастамалары, 10 сынып.
Тараз. ТарГУ, 2000ж. 25-41 беттер.
10. А.Н.Колмогоров. Алгебра және анализ бастамалары, 10 сынып.
Алматы. Рауан, 1992 ж. 159-160 беттер.
11. А.Е.Әбілқасымова, К.Д.Шойынбеков, М.И.Есенова, З.А.Жұмағұлова.
Алгебра және анализ бастамалары, 10 сынып.
Алматы:Мектеп, 2006 ж. 135 бет.
Мазмұны
Кіріспе
1. Функция ұғымы тарихынан
Негізгі бөлім
1. Функция
2. Функцияның берілу тәсілдері.
3. Функциялардың қарапайым сипаттамалары.
4. Кубтық функция және оны туындының көмегінсіз зерттеу жолдары.
5. Функцияны туындының көмегімен зерттеу жолдары.
Қорытынды
Пайдаланылған әдебиеттер
Қ.Сәтбаев атындағы
шағын орталықты орта
мектебінің 11 «ә» сынып
оқушысы Сағындық Ұлмекеннің
«Кубтық функция»атты ғылыми жұмысына
Пікір
Оқушының таңдаған тақырыбы – мектеп бағдарламасындағы функцияны зерттеуді пайдаланып, кубтық функцияны дәлелдеуді қарастырған.
Мектеп курсында негізінен функцияны зерттеу туындының көмегінсіз шешу әдістерін білу оқушылар үшін өте қажет. Осыған байланысты жұмыста қарастырылатын мәселені мектеп оқушылары үшін өте пайдалы деп есептеуге болады.
Сағындық Ұлмекен өз бетінше кубтық функцияларды зерттеудің жолдарын салыстыра отырып қарастырған және олардың басқа әдістерін іздестірген.
Кубтық функцияны экстремумдарды табу дискриминантқа
(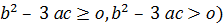 байланысты екенін дәлелдеп, әр түрлі есептер шешілген. Бұл білімдердің өз бетімен жұмыс істеуге қабілетті екенін көрсетеді.
байланысты екенін дәлелдеп, әр түрлі есептер шешілген. Бұл білімдердің өз бетімен жұмыс істеуге қабілетті екенін көрсетеді.
Келтірілген материалдарды оқып шығып, бір жүйеде жазудың өзі көптеген еңбек сіңіруді талап еткені көрініп тұр. Жұмысты орындау барысында Сағындық Ұлмекен көптеген әдебиеттерді оқып шығып, ой елегінен өткізіп, талдап, зерттеп, көп еңбек сіңіргені байқалып тұр.
Жұмыс өз мақсатына жеткен. Жұмыста функциялар толығымен қарастырылып, бір-бірімен салыстырылып, математикалық тұрғыдан зерттелінген.
Пікір жазған: Аты-жөні
Қ.Сәтбаев атындағы шағын орталықты орта мектебінің 11 «ә» сынып оқушысы Сағындық Ұлмекеннің «Кубтық функция» тақырыбындағы ғылыми жұмысының зерттеу күнделігі.
| Р/с | Атқарылған іс-шаралар | Мерзімі |
| Тақырыпты нақтылау | 5.09.14 | |
| Тақырыпқа байланысты әдебиеттермен танысу, талдап саралау, картотека даярлау. | 6.10.14 | |
| Жұмыстың жоспарын жасау. | 10.12.14 | |
| Жоспар бойынша жұмыс. | 12.01.15 | |
| Функция жайлы мәліметтер жинау. | 15.01.15 | |
| Функцияны зерттеудің әр түрлі әдістерін зертеу. | 5.02.15 | |
| Ғылыми жоба жұмысын мектеп ғылыми жобалар жарысында өткізу. | 10.04.15 | |
| Жұмысқа қосымшалар енгізу. Тақырыпқа байланысты көрнекіліктер жасау. | 12.04.15 | |
| Жұмысты редакциядан өткізу. | 20.04.15 |
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ Т.РЫСҚҰЛОВ АУДАНЫ ӘКІМДІГІНІҢ БІЛІМ БӨЛІМ Қ.СӘТБАЕВ АТЫНДАҒЫ ШАҒЫН ОРТАЛЫҚТЫ ОРТА МЕКТЕБІ.
Орындаған: Сағындық Ұлмекен Жанболатқызы
11 «ә» сынып оқушысы
Тақырыбы: Кубтық функция
Бағыты: Экономикалық және әлеуметтік процестерді
математикалық модельдеу.
Секция: Математика
Жетекшісі: Математика пәнінің мұғалімі:
Бейсетаева Раушан Нұрманалықызы
Жаңатұрмыс ауылы
2014-2015ж.
 2015-08-12
2015-08-12 1600
1600







