Plane problems

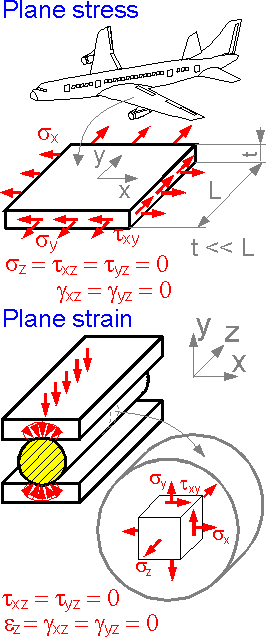
There are two special states of stress: plane stress for thin plates and plane strain for thick plates.

For plane stress there are four non-zero strain components (e_x, e_y, e_z, g_xy) and three non-zero stress components (s_x, s_y, t_xy). The plane stress is typical for thin-walled structures such as in airplane wings.

For plane strain there are three non-zero strain components (e_x, e_y, g_xy) and four non-zero stress components (s_x, s_y, s_z, t_xy). Plane strain is typical for thick plates.

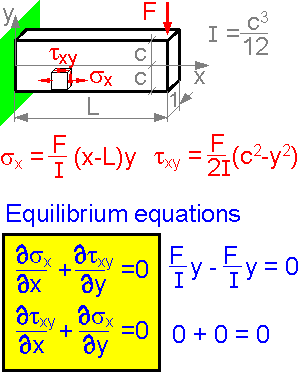There are two equilibrium equations that must be satisfied for absence of mass forces. Elastic plates have stress fields that satisfy Hooke's law and the strain compatibility equations. The two stress components shown correspond to an embedded beam with a force applied to the right end. The equilibrium equations help solve the plane problems of the theory of elasticity.

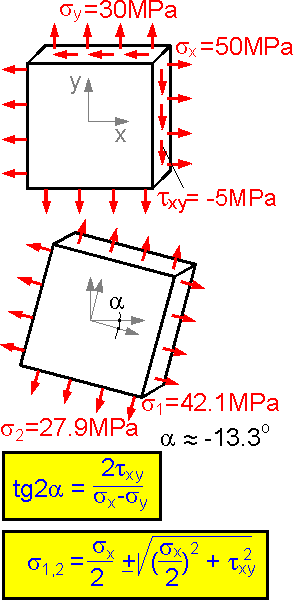There are two inclined principle planes where there is no shear stress and normal stresses (s₁ and s₂) are at a maximum.

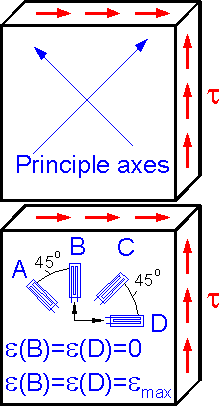Principle axes are inclined 45^o to the direction of shear stress t for pure shear. Indication A is negative. There are zero indications for B and D.

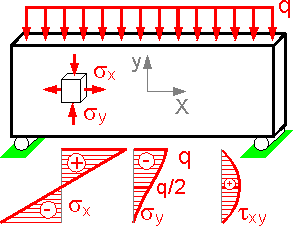The figure shows typical stress patterns for s_x, s_y and t_xy. The normal stress sx is usually higher than other stress components for a long beam, where Length >> Height.

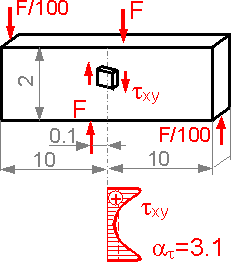There is concentration of shear stress in the area where force is applied. Shear stress is equal to zero at the surface and is at a maximum in a neighboring region.

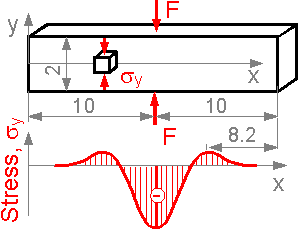Normal stress s_y at axis x can be positive outside the zone of compression. Here, the compressive stress is significantly higher than the tensile stress.

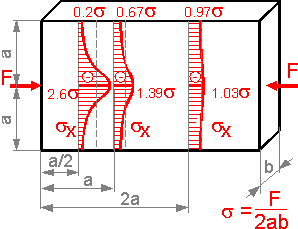Saint-Venant's principle. At a distance equal to width of the beam (2a), the maximum stress does not exceed the nominal stress by 4%. The stress pattern becomes practically uniform.