Finite elements

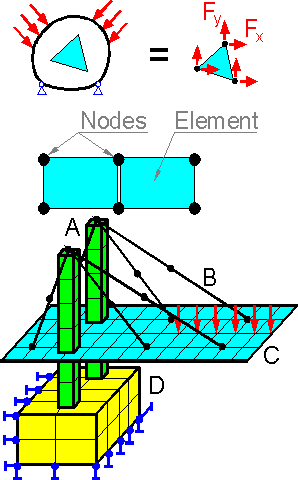
The mathematical model is subdivided by finite elements which are connected to each other with nodes. Forces act at the nodes. The finite element is not a rigid body, the model assumes stresses and strains exist inside the finite elements.

There are a few commonly-used finite elements: beam A, truss B, thin shell C, 2D or 3D continuum (D). It is possible to use several types of elements in one model.

Reliability of the FEA predictions depends on the number of finite elements. If the inner stresses do not vary greatly then the number of elements does not have a significant effect on the accuracy.

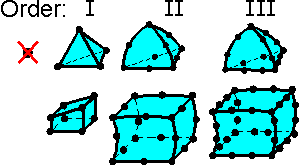Solid elements may be linear (first-order elements) or parabolic (second-order elements). Linear elements have corner nodes only and their edges are straight. The minimum number of nodes for 3D elements is 4. Parabolic elements can have a node placed centrally along each edge and therefore the edges are parabolic. Given the same number of elements, the higher order elements are more accurate because they have a more complex mathematical formulation to describe the element shape (shape function). Also, they represent curved geometry more accurately. An analysis involving higher order elements requires more computational resources.

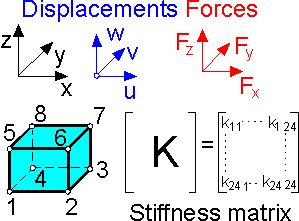There are 3 degrees of freedom in a node and 8 nodes for a brick (hexahedral) element. This means that 24 nodal displacements and 24 nodal forces must be considered. The size of the stiffness matrix that relates the nodal displacement vector with the nodal forces vector is [24*24].

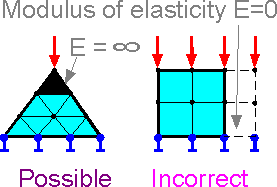The stiffness matrix components are inversely proportion to the modulus of elasticity. Zero modulus of elasticity means that there is no finite elements. Division by zero modulus of elasticity leads to numerical errors in the FEM procedures. Infinity modulus of elasticity means that a part of structure is absolutely rigid.

Although in the theory of elasticity the tensile stress in the crack tip is equal to infinity, all stresses are finite in FEM.

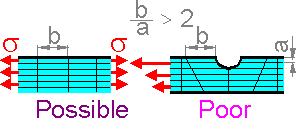Long elements can be used if there is not a large gradient of displacements, strains and stresses. Such elements can be used in fields of uniform stress but not for stress concentrations. The stress gradient is high but still finite in zones of stress concentration.

If a structure and its loads are symmetrical about the axis the problem can be solved using axisymmetric 2D finite elements.

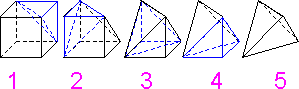Five tetrahedral elements are enough to form a cube. Parabolic pyramid elements provide results that are at least as accurate as linear brick elements.