Parts of a circle include its diameter, circumference, radius, chord, arc, and sector. To explore the properties of a circle, wrap a string around a soda can and measure the length of the string (the circumference of the circle formed by the string). Then lay the string directly across the top of the soda can so that it divides the top in half. Measure the string’s length (the diameter of the circle formed by the top of the can). Divide the circumference (C) by the diameter (D). Do this for several circles. You should find that the ratio of C/D is about 3:1 for all of your circles, both large and small. This ratio is often represented by the symbol p. Another experiment compares running around the circumference of a circular track to heading directly across along its diameter. For every 3 steps around the circular track, a runner only needs to take 1 step directly across.
Parabola
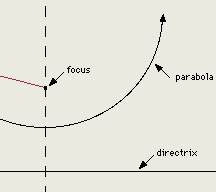
Parabola, in mathematics, plane curve formed by the intersection of a cone with a plane parallel to a straight line on the slanting surface of the cone (see Geometry). Each point of the curve is equidistant from a fixed point, called the focus, and a fixed straight line, known as the directrix. The parabola is symmetrical about a line passing through the focus and perpendicular to the directrix. For a parabola symmetric about the x-axis and with its vertex at the origin, the mathematical equation is y 2 = 2 px, in which p is the distance between the focus and the directrix.
A parabola is the curve that describes the trajectory of a projectile, such as a bullet or a ball, in the absence of air resistance. Because of air resistance, however, the curves in which projectiles travel only approximate true parabolas. Parabolic mirrors are reflectors that have the shape of a parabola rotated about the parabola's axis of symmetry. Parabolic mirrors reflect rays of light in parallel lines from a light source at the mirror's focus. Such reflectors are used in automobile headlights and all other forms of searchlights. Parabolic mirrors also bring parallel rays of light to a focus without spherical aberration (see Optics). This type of reflector is therefore valuable in astronomical telescopes (see Telescope). Parabolic reflectors are used also as antennas in radio astronomy and radar.
 2015-08-21
2015-08-21 296
296