2015-08-21
287
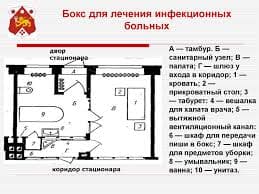
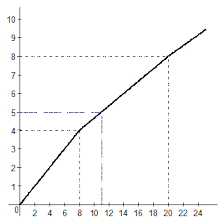
Let's assume that the location of a subscriber network where they introduce the stationary radio access to the reference node of a base network is given. It is necessary to define among subscriber network points the location of base station (BS), which connects with subscriber points (SP) through radio channels. It is desirable to have minimal distance from BS to any SP that will provide a stable radio communication with smaller power of BS transmitter. It is clear that such criterion is impossible to satisfy therefore it is necessary to minimize the distance to the most remote point. It is thus expedient the BS whenever possibly to occupy the central position under the relation to all RP.
The problem of finding such point can be turn to a problem of the graph centre finding.
D e f i n i t i o n. Let G (N, V) be a graph, where N – set of vertices, and V – set of distances between all vertices.
The vertex s is called the graph G (N, V) centre if it satisfies to a condition max lsj m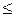 
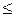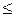max lij for any i; 1 j n.
The algorithm of finding graph centre (vertex s) follows from the definition:
Step 1. In each line of an initial weighted matrix L = [ lij ] – find element with the maximum value.
Step 2. Among set of the maximum values of lines elements find the least lsj {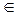 
lij }. The vertex s is the graph centre.
Thus, having minimized the distance from a point s to the most remote vertex, we provided to all other vertices guaranteed smaller distance.
