Particles energy distribution. Distribution functions

In order to determine the number of free charge carriers in a semiconductor, it is necessary to know the number of occupied levels (stages) in the conduction band and the number of free levels in the valence band. The probability that the electron position is on a certain energy level W can be found from the Fermi-Dirac distribution function

,

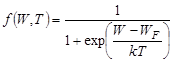where k is Boltzmonn’s constant, T is absolute temperature, W_F is the Fermi energy level.

The distribution function f (W,T) for the level W= W_F at T 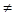0K is equal to one half. So, the Fermi level is the energy level whose occupation probability at temperature which differs from absolute zero is one half.

At T=0K the Fermi –Dirac distribution function for energy levels located below the Fermi energy level is equal to unity since 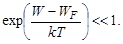This demonstrates that all levels located below the Fermi level are occupied by electrons at the temperature of absolute zero. For energy levels located above the Fermi level, this distribution function comes to zero because 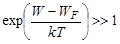, i.e. at absolute zero all the levels found above the Fermi level are empty.

When the external effects are absent and T=0K, semiconductors have their valence bands completely occupied and conduction bands are empty. This suggests that the Fermi level of semiconductors lies in the energy gap. Calculations show that in intrinsic semiconductors the Fermi level is located almost in the middle of the forbidden band:

,

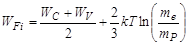where m_e and m_p are the effective mass of electrons and hole respectively.

We may conclude that the Fermi level of an intrinsic semiconductor lies approximately in the middle of the band gap, and its position depends on the electron-to-hole effective mass relation (Fig.2.4 a). In electronic semiconductors the Fermi level is located near the bottom of the conduction band, whereas in hole semiconductor it lies near the top of the valence band (Fig. 2.4 b, c).

In semiconductors, energy needed to transfer electrons to the conduction band generally differs substantially in value from the energy of the Fermi level. The difference (W-W_F) is as a rule three times as high as the value of kT. Therefore, 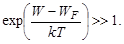Hence,

.

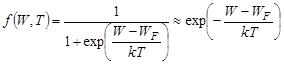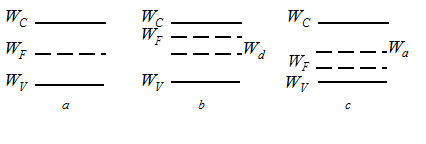
Fig.2.4. The Fermi level location in: a – intrinsic, b – electronic,

c – hole semiconductors

Denoting exp(W_F/kT) by C, we get 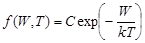, i.e. in this case the behaviour of semiconductor elements obeys the classical Maxwell-Boltzmann statistics.

The similar conclusion can be made for holes if we regard the probability of a hole appearance as the probability that a given energy level is empty.

If we designate the Fermi-Dirac distribution function as f_n for electrons and as f_p for holes, then f_n+f_p=1. When the electrons and holes behaviour in a semiconductor follows the Maxwell-Boltzmann statistics, the semiconductor is considered as non-degenerated. However, the condition of 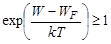does not always occur. This case corresponds to a semiconductor operating at a high temperature or a highly-doped semiconductor with a narrow-gap. Here the Fermi level is found to lie either in the valence band or in the conduction band. Such semiconductors are termed degenerated, for which the Maxwell-Boltzmann statistics are not applicable. The electrons and holes energy distribution can be described by the Fermi-Dirac distribution function.