Свойства базисных функций элемента

В общем случае элементные аппроксимирующие функции 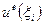должны быть непрерывными, а их производные до 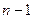порядка – непрерывными или постоянными внутри элемента и между элементами ( 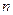– порядок старшей производной в дифференциальном уравнении краевой задачи). Вследствие того, что по версии МКЭ:

; ,

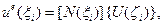
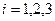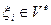указанными свойствами должны обладать и базисные функции 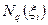элемента .

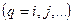Так как узловые значения функции 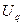– это числа с размерностью искомой физической величины 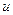, базисные функции элемента должны быть безразмерными. В этом нетрудно убедиться, проанализировав формулы предыдущих параграфов этой главы.

Подставив в базисную функцию (4.2.4) координаты 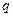-го узла, получим:

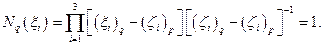
Если в выражение (4.2.4) подставить координаты 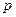-х узлов 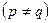, то оно даст 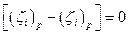. Таким образом, базисная функция должна удовлетворять следующим необходимым условиям:

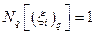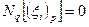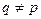, , . (4.5.1)

Просуммируем столбцы матрицы 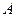(4.1.6), описывающие коэффициенты базисных функций (4.1.7) симплекс-треугольника:

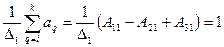, так как ;

;

.

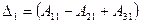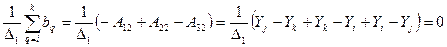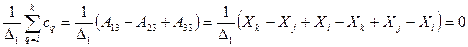Из этих равенств вытекает еще одно необходимое условие, которому должны удовлетворять базисные функции произвольного (а не только треугольного) элемента с произвольным количеством 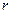узлов:

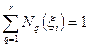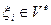, , (4.5.2)

которое может быть отнесено к нормировочному.

Нарушение требования (4.5.2) однозначно свидетельствует, что какие-то (или все) базисные функции элемента определены неверно.

Градиент искомой физической величины 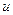определяется производными базисных функций и узловыми значениями :

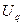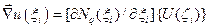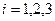, . (4.5.3)

Согласно (4.2.4) и (4.3.1) первые производные базисных функций элементов каталога будут содержать оставшиеся после дифференцирования текущие переменные и их произведения в первой степени. Такие элементы принято называть мультиплекс-элементами. У этих элементов непрерывными являются и первые производные базисных функций, но только по двум переменным, а вторые производные по этим же переменным постоянны.

У линейного тетраэдра (и треугольника), как видно из (4.1.14), первые производные базисных функций постоянны и равны коэффициентам 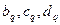при текущих переменных. Такие элементы называют симплекс-элементами (простыми). Как было показано выше, суммы коэффициентов 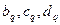равны нулю. Следовательно, для произвольного симплекс-элемента с 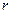узлами имеем:

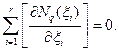(4.5.4)

Соотношение (4.5.4) можно считать одним из признаков принадлежности элемента к семейству симплекс-элементов.

Постоянство градиента внутри симплекс-элемента требует использования малых по размерам элементов, чтобы точнее аппроксимировать быстро меняющуюся функцию 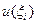. Автоматически это обусловливает дискретизацию исследуемой области на большое число элементов со всеми вытекающими отсюда последствиями.

В заключение еще раз заметим, что элементы принято классифицировать на лагранжевы и эрмитовы в зависимости от того, включает ли узловой вектор только значения функции – лагранжевы, или и значения ее производных – эрмитовы элементы [6]. Все элементы базового каталога по этой классифи­кации являются лагранжевыми.