Решим симплекс-методом задачу с искусственным базисом (хотя бы один знак неравенств-ограничений " ≥ " или " = ").
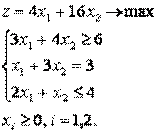
Запишем задачу в канонической форме (в виде системы уравнений, что требует симплекс-метод), для этого введем две переменные х3 ≥ 0 и х4 ≥ 0 получим:
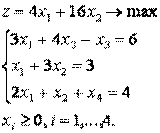
Система ограничений предлагает только одну допустимую базисную переменную x 4, только она входит только в одно уравнение в третье с коэффициентом 1, поэтому в первое и второе уравнения добавляем искусственные переменные R 1 ≥ 0 и R 2 ≥ 0 Чтобы можно было применить симплекс-метод система уравнений-ограничений должна быть системой с базисом, т.е. в каждом уравнении должна быть переменная с коэффициентом 1, которая входит только в одно уравнение системы, в нашем случае это R 1, R 2 и x 4. Получили, так называемую, М -задачу:
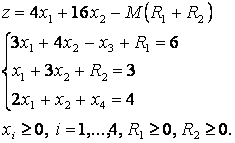
Данная система является системой с базисом, в которой R 1, R 2 и x 4 базисные переменные, а x 1, x 2 и x 3 свободные переменные, свободные члены всех уравнений неотрицательны. Следовательно, для решения задачи можно применить симплекс-метод. Запишем начальную симплекс-таблицу:
|
|
|
симплекс-метод итерация 0
| БП | x 1 | x 2 | x 3 | R 1 | R 2 | x 4 | Решение | Отношение |
| z | −4 | −16 | − | |||||
| R 1 | −1 | 6/4=3/2 | ||||||
| R 2 | 3/3=1 | |||||||
| x 4 | 4/1=4 | |||||||
| Оценка | −4 | −7 | −1 | −1 | − | − |
В таблицу для задач с искусственным базисом добавлена строка «Оценка». Она получается суммированием соответствующих коэффициентов строк с искусственными переменными (R) с противополжным знаком. Она будет присутствовать в таблице до тех пор, пока хотя бы одна из искусственных переменных есть в базисе. По наибольшему по модулю отрицательному коэффициенту строки "Оценка" определяется разрешающий столбец пока она есть в таблице. Когда строка "Оценка" выйдет из таблицы (в базисе нет искусственных переменных) разрешающий столбец будет определяться по z-строке, как и в задаче с начальным базисом. В данной таблице разрешающий столбец х2, он выбран по наибольшей по модулю отрицательной оценке (−7). Разрешающая строка R 2 выбрана по наименьшему отношению столбца "Решение" к соответствующим положительным элементам разрешающего столбца, как и в задаче без искусственных переменных. Это значит, что на следующей итерации симплекс-метода переменная х 2 из свободной перейдет в базисную, а переменная R 2 из базисной – в свободную. Запишем следующую симплекс-таблицу:
Симплекс-метод итерация 1
| БП | x 1 | x 2 | x 3 | R 1 | R 2 | x 4 | Решение | Отношение |
| z | 4/3 | 16/30 | − | |||||
| R 1 | 5/3 | −1 | −4/3 | 6/5 | ||||
| x 2 | 1/3 | 1/3 | ||||||
| x 4 | 5/3 | −1/3 | 9/5 | |||||
| Оценка | −5/3 | −1 | 4/3 | − | − |
Разрешающий столбец х 1, разрешающая строка R 1, R 1 выходит из базиса, x 1 входит в базис. После этого в базисе не остается искусственных переменных, поэтому строки «Оценка» в следующей таблице нет:
|
|
|
Симплекс-метод итерация 2
| БП | x 1 | x 2 | x 3 | R 1 | R 2 | x 4 | Решение | Отношение |
| z | 4/5 | −4/5 | 32/5 | 72/5 | − | |||
| x 1 | −3/5 | 3/5 | −4/5 | 6/5 | − | |||
| x 2 | 1/5 | −1/5 | 3/5 | 3/5 | − | |||
| x 4 | −1 | − |
Далее разрешающий столбец выбирается по z -строке. В z -строке все коэффициенты неотрицательны кроме коэффициента при искусственной переменной R 1, который не влияет на оптимальность, когда искусственные переменные вышли из базиса. Следовательно, симплекс-методом получено оптимальное решение x 1 = 6/5; x 2 = 3/5; zmax = 72/5.
Особые случаи применения симплекс-метода
1) Когда прямая (если рассматривается двухмерная задача линейного программирования, а в общем случае гиперплоскость), представляющая целевую функцию параллельна прямой (гиперплоскости), соответствующей одному из неравенств-ограничений (которое в точке оптимума выполняется, как точное равенство) целевая функция принимает одно и тоже оптимальное значение на некотором множестве точек границы области допустимых решений. Эти решения называются альтернативными оптимальными решениями. Наличие альтернативных решений можно определить по оптимальной симплекс-таблице. Если в z -строке оптимальной таблицы есть нулевые коэффициенты небазисных переменных, то есть альтернативные решения.
2) Если в разрешающем столбце симплекс-таблицы все коэффициенты меньше или равны нуль, то нельзя выбрать разрешающую строку, в этом случае решение неограничено.
3) Если ограничения задачи линейного программирования несовместны (т.е. они не могут выполняться одновременно), то задача не имеет допустимых решений. Такая ситуация не может возникнуть, если все неравенства, составляющие систему ограничений, имеют тип " ≤ " с неотрицательными правыми частями, т.к. в этом случае дополнительные переменные могут составить допустимое решение. Для других типов ограничений используются искусственные переменные. Если задача имеет решение, то в оптимальной таблице в базисе нет искусственных переменных (R i). Если они там есть, то задача не имеет решений.
 2015-08-21
2015-08-21 224
224







