1) егер 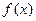 функциясы үшін
функциясы үшін 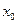 нүктесінің
нүктесінің 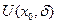 маңайында
маңайында 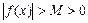 теңсіздігі орындалып, ал
теңсіздігі орындалып, ал 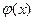 функциясы үшін
функциясы үшін 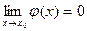
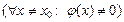 болса, онда
болса, онда 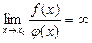 ;
;
2) егер 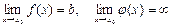 болса, онда
болса, онда 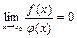 .
.
Салдар. Егер 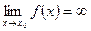 болса, онда
болса, онда 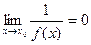 .
.
3. Шегі бар функциялардың қасиеттері
6- теорема. Егер  функциясының
функциясының 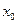 нүктесінде
нүктесінде 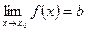 нақты мәнді шегі бар болса, онда:
нақты мәнді шегі бар болса, онда:
1) 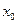 нүктесінің
нүктесінің 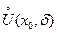 ойылған маңайында
ойылған маңайында  функциясы шенелген;
функциясы шенелген;
2) егер 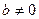 болса, онда функцияның мәндері де
болса, онда функцияның мәндері де 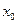 нүктесінің
нүктесінің 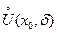 ойылған маңайында
ойылған маңайында 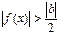 болады. Нақтырақ айтқанда,
болады. Нақтырақ айтқанда, 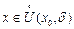 үшін егер
үшін егер 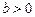 болса, онда
болса, онда 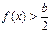 , ал егер
, ал егер 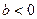 болса, онда
болса, онда 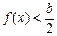 ;
;
3) егер 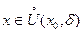 үшін
үшін 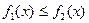 және
және 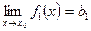 ,
, 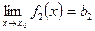 болса, онда
болса, онда 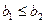 ;
;
4) егер 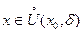 үшін
үшін 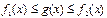 және
және 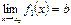 ,
, 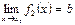 болса, онда
болса, онда 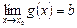 ;
;
5) егер 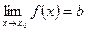 ,
, 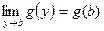 болса, онда
болса, онда 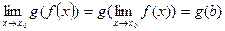 ;
;
6) егер 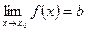 ,
, 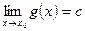 болса, онда:
болса, онда:
а) 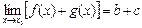 , б)
, б) 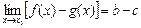 , с)
, с) 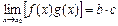 , d) егер с¹ 0 болса, онда
, d) егер с¹ 0 болса, онда 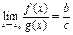 болады.
болады.
Ескерту. а) мен с) теңдіктері екі функция үшін ғана емес, кез келген ақырлы қосынды мен көбейтінді үшін де о р ындалады.
4. Тамаша шектер. Бiрiншi тамаша шек 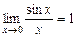
Екiншi тамаша шек 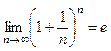 немесе
немесе 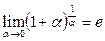 .
.
5. Функциялардың үзіліссіздігі мен үзілуі
Анықтама. Егер кез келген 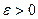 саны бойынша
саны бойынша 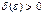 саны табылып,
саны табылып, 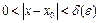 , теңсіздіктерін қанағаттандыратын барлық
, теңсіздіктерін қанағаттандыратын барлық 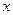 үшін
үшін 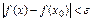 теңсіздігі орындалатын болса, онда
теңсіздігі орындалатын болса, онда 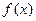 функциясын
функциясын 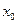 нүктесінде үзіліссіз деп атайды. Яғни,
нүктесінде үзіліссіз деп атайды. Яғни,
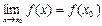 (2).
(2).
Кванторлар тілінде 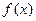 функциясының
функциясының  нүктесінде үзіліссіздігі былай жазылады:
нүктесінде үзіліссіздігі былай жазылады:
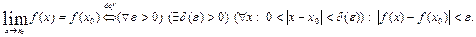
Жоғарыда берілген анықтамадан, 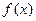 функциясының
функциясының  нүктеде үзіліссіздігі келесі үш шарттың орындалуын білдіреді:
нүктеде үзіліссіздігі келесі үш шарттың орындалуын білдіреді:
1)  функциясы
функциясы  нүктесінде және оның қандай да бір
нүктесінде және оның қандай да бір 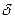 маңайында анықталған;
маңайында анықталған;
2)  функциясының
функциясының  нүктесінде шегі бар;
нүктесінде шегі бар;
3)  функциясының
функциясының  нүктесіндегі шегі функцияның сол нүктедегі мәніне тең.
нүктесіндегі шегі функцияның сол нүктедегі мәніне тең.
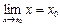 болғандықтан, үзіліссіздіктің анықтамасындағы (2)-теңдікті былай да
болғандықтан, үзіліссіздіктің анықтамасындағы (2)-теңдікті былай да 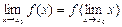 жазуға болады.
жазуға болады.
Демек, үзіліссіздікті шек таңбасы «lim» пен функция белгісі 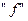 - ті өзара орын ауыстыру мүмкіндігі деп те анықтауға болады.
- ті өзара орын ауыстыру мүмкіндігі деп те анықтауға болады.
(2) - теңдікті 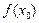 - ді теңдіктің сол жағына шек таңбасының астына көшіріп,
- ді теңдіктің сол жағына шек таңбасының астына көшіріп, 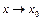 болса
болса 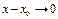 екендігін ескеріп,
екендігін ескеріп,
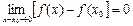 (3)
(3)
түрінде жаза аламыз. Мұндағы, 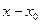 айырымын аргументтің өсімшесі, ал
айырымын аргументтің өсімшесі, ал 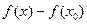 айырымын функцияның өсімшесі деп атайды.
айырымын функцияның өсімшесі деп атайды.
Егер 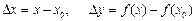 арқылы белгілесек, онда
арқылы белгілесек, онда 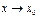 болса
болса 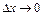 болатындықтан (3) - ті келесідей жаза аламыз:
болатындықтан (3) - ті келесідей жаза аламыз:
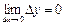 (4)
(4)
«Өсімше» терминін қолданып, үзіліссіздіктің анықтамасын былай айтуға болады: егер тәуелсіз айнымалының 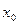 нүктедегі өсімшесі
нүктедегі өсімшесі 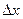 нөлге ұмтылғанда, оған сәйкес
нөлге ұмтылғанда, оған сәйкес  функциясының өсімшесі
функциясының өсімшесі 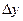 нөлге ұмтылса, онда
нөлге ұмтылса, онда  функциясын
функциясын 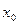 нүктесінде үзіліссіз деп атайды.
нүктесінде үзіліссіз деп атайды.
Мысалы, 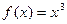 функциясы
функциясы 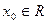 үшін үзілліссіз.
үшін үзілліссіз.
Шынында да,
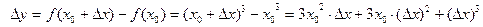 болғандықтан
болғандықтан 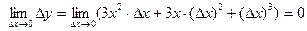 . Демек,
. Демек, 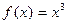 функциясы кез-келген
функциясы кез-келген 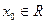 нүктесінде үзіліссіз.
нүктесінде үзіліссіз.
Егер 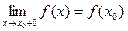 болса, онда
болса, онда 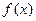 функциясын
функциясын 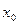 нүктесінде оң жақты үзіліссіз деп атайды;
нүктесінде оң жақты үзіліссіз деп атайды;
егер 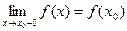 болса, онда
болса, онда 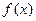 функциясын
функциясын 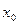 нүктесінде сол жақты үзіліссіз деп атайды.
нүктесінде сол жақты үзіліссіз деп атайды.
Егер  функциясының анықталу аралығы
функциясының анықталу аралығы 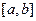 сегменті болса, онда
сегменті болса, онда  функциясының
функциясының 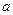 нүктесінде тек қана оң жақты, ал
нүктесінде тек қана оң жақты, ал 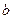 нүктесінде тек қана сол жақты үзіліссіздігі туралы айтуға болады.
нүктесінде тек қана сол жақты үзіліссіздігі туралы айтуға болады.
Үзіліссіз функциялардың кейбір қасиеттері
7-теорема. Егер 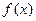 функциясы
функциясы 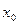 нүктесінде үзіліссіз болса, онда
нүктесінде үзіліссіз болса, онда 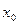 нүктесінің қандай да бір
нүктесінің қандай да бір 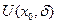 маңайында:
маңайында:
1)  функциясышенелген;
функциясышенелген;
2) 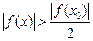 . Нақтырақ айтқанда, егер
. Нақтырақ айтқанда, егер 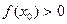 болса, онда
болса, онда 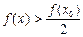 , ал егер
, ал егер 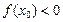 болса, онда
болса, онда 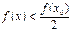 ;
;
3) егер 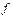 және
және 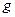 функциялары
функциялары 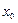 нүктесінде үзіліссіз болса, онда
нүктесінде үзіліссіз болса, онда 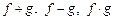 және
және 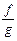
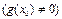 функциялары да сол нүктелерде үзіліссіз;
функциялары да сол нүктелерде үзіліссіз;
4) егер 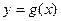 функциясы
функциясы 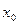 нүктесінде, ал
нүктесінде, ал 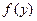 функциясы
функциясы 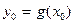 нүктесінде үзіліссіз болса, онда күрделі
нүктесінде үзіліссіз болса, онда күрделі 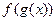 функциясы
функциясы 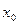 нүктесінде үзіліссіз болады.
нүктесінде үзіліссіз болады.
Анықтама. Егер  функциясы
функциясы  нүктесінде анықталмаса немесе
нүктесінде анықталмаса немесе  нүктесі анықталу жиынында жатып,
нүктесі анықталу жиынында жатып,  сол нүктеде үзіліссіз болмаса, онда
сол нүктеде үзіліссіз болмаса, онда  нүктесін
нүктесін  -тің үзіліс нүктесі деп атап,
-тің үзіліс нүктесі деп атап,  -ті
-ті  нүктесінде үзіледі дейді.
нүктесінде үзіледі дейді.
Анықтама. Егер  нүктесі
нүктесі  функциясының үзіліс нүктесі болып, сол нүктеде біржақты ақырлы шектері
функциясының үзіліс нүктесі болып, сол нүктеде біржақты ақырлы шектері
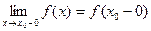 ,
, 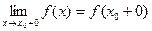
бар болса, онда  функциясы
функциясы  нүктесінде жай немесе бірінші түрдегі үзілісті дейді.
нүктесінде жай немесе бірінші түрдегі үзілісті дейді.
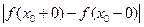 санын
санын  функциясының
функциясының 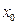 нүктесіндегі секірмесі деп атайды.
нүктесіндегі секірмесі деп атайды.
Егер 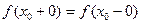 болса онда
болса онда 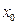 - ді жөнделетін үзіліс нүктесі деп атайды.
- ді жөнделетін үзіліс нүктесі деп атайды.
Егер  функциясы
функциясы  нүктесінде үзілісті болып, бірақ үзілісі бірінші түрдегі үзіліс болмаса, дәлірек айтқанда,
нүктесінде үзілісті болып, бірақ үзілісі бірінші түрдегі үзіліс болмаса, дәлірек айтқанда,  нүктесінде
нүктесінде  - тің кемінде бір біржақты ақырлы шегі болмаса, онда
- тің кемінде бір біржақты ақырлы шегі болмаса, онда  функциясын
функциясын  нүктесінде күрделі немесе екіншітүрдегі үзілісті дейді.
нүктесінде күрделі немесе екіншітүрдегі үзілісті дейді.
Сонымен,  функциясы
функциясы  нүктесінде үзіліссіз болуы үшін
нүктесінде үзіліссіз болуы үшін 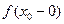 ,
, 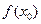 ,
, 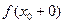 сандарының мағыналы болып, олардың өзара тең болуы қажетті және жеткілікті, яғни
сандарының мағыналы болып, олардың өзара тең болуы қажетті және жеткілікті, яғни 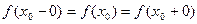 .
.
Мысалдар. 1. 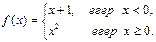 функциясын
функциясын 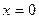 нүктесінде үзіліссіздікке зерттеңіз.
нүктесінде үзіліссіздікке зерттеңіз.
Шешуі. 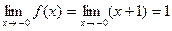 ,
, 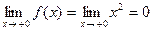 .
.
Функцияның 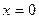 нүктесіндегі біржақты шектері ақырлы, бірақ өзара тең емес. Демек,
нүктесіндегі біржақты шектері ақырлы, бірақ өзара тең емес. Демек, 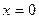 бірінші түрдегі үзіліс нүктесі.
бірінші түрдегі үзіліс нүктесі.
2. 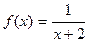 функция
функция 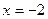 нүктесінде анықталмаған. Осы нүктедегі үзілісті зерттеңіз.
нүктесінде анықталмаған. Осы нүктедегі үзілісті зерттеңіз.
Шешуі. 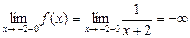 ,
, 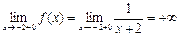 болғандықтан,
болғандықтан, 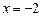 нүктесіекіншітүрдегі үзіліс нүктесі.
нүктесіекіншітүрдегі үзіліс нүктесі.
Негізгі элементар функциялар өздерінің анықталу жиынында үзіліссіз.
Кесіндіде үзіліссіз функциялар
Анықтама. 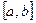 кесіндісінің әрбір нүктесінде үзіліссіз
кесіндісінің әрбір нүктесінде үзіліссіз  функциясын кесіндіде үзіліссіз функция дейді.
функциясын кесіндіде үзіліссіз функция дейді.
Басқа аралықтарда үзіліссіз функция да осы сияқты анықталады.
8-теорема (Вейерштрасстың бірінші теоремасы). Егер 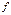 функциясы
функциясы 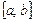 кесіндіде анықталған және үзіліссіз болса, онда оның мәндерінің жиыны шенелген жиын болады.
кесіндіде анықталған және үзіліссіз болса, онда оның мәндерінің жиыны шенелген жиын болады.
9-теорема (Вейерштрасстың екінші теоремасы). Егер 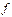 функциясы
функциясы 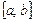 кесіндіде анықталған және үзіліссіз болса, онда осы кесіндіде ол ең үлкен және ең кіші мәндерін қабылдайды.
кесіндіде анықталған және үзіліссіз болса, онда осы кесіндіде ол ең үлкен және ең кіші мәндерін қабылдайды.
10-теорема (Больцано-Коши). Егер  функциясы
функциясы 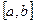 сегментінде үзіліссіз болып, сегменттің ұштарындағы мәндері
сегментінде үзіліссіз болып, сегменттің ұштарындағы мәндері 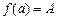 ,
, 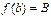 болса, онда
болса, онда 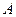 мен
мен 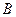 - ның арасында жатқан кез келген
- ның арасында жатқан кез келген 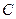 үшін
үшін 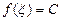 теңдігін қанағаттандыратын кемінде бір
теңдігін қанағаттандыратын кемінде бір 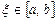 нүктесі табылады.
нүктесі табылады.
Мысалдар. 1. 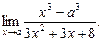 Берілген өрнек
Берілген өрнек 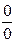 түріндегі анықталмағандық.
түріндегі анықталмағандық. 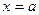 болғанда алымы мен бөлімі нөлге тең болатындықтан, олар
болғанда алымы мен бөлімі нөлге тең болатындықтан, олар 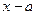 -ға бөлінеді. Сондықтан,
-ға бөлінеді. Сондықтан,
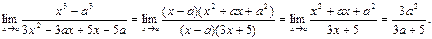
2. 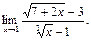 Берілген шекті есептеу үшін
Берілген шекті есептеу үшін 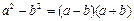 және
және 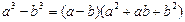 формулаларына сүйенеміз. Бөлшектің алымы мен бөлімін
формулаларына сүйенеміз. Бөлшектің алымы мен бөлімін 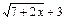 және
және 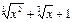 өрнектеріне көбейтіп, ортақ көбейткішке қысқартамыз. Сонда,
өрнектеріне көбейтіп, ортақ көбейткішке қысқартамыз. Сонда,
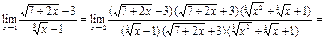
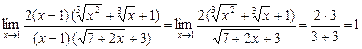 .
.
3. 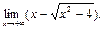 Берілген өрнек
Берілген өрнек 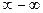 түріндегі анықталмағандық.
түріндегі анықталмағандық. 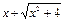 қосындысына көбейтсек және бөлсек, онда
қосындысына көбейтсек және бөлсек, онда
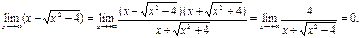
4. 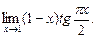 Берілген өрнек
Берілген өрнек  түріндегі анықталмағандық.
түріндегі анықталмағандық. 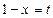 деп белгілесек, онда
деп белгілесек, онда 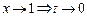 . Бірінші тамаша шекті ескерсек, келесідей болады:
. Бірінші тамаша шекті ескерсек, келесідей болады:
5. 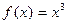 функциясы
функциясы 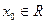 үшін үзілліссіз.
үшін үзілліссіз.
Шынында да, 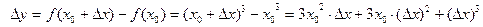 болғандықтан
болғандықтан 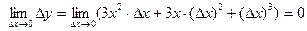 . Демек,
. Демек, 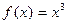 функциясы кез-келген
функциясы кез-келген 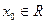 нүктесінде үзіліссіз.
нүктесінде үзіліссіз.
6. tg x функциясы өзінің анықталу жиынында үзіліссіз, яғни барлық 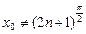 (n=0, ±1, …) сандары үшін мына теңдік
(n=0, ±1, …) сандары үшін мына теңдік 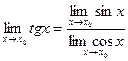 =
= 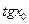 дұрыс.
дұрыс.
Әрине, әрбір есепті шығарғанда шығармашылық танытып әртүрлі әдістерді аралас қолдануға болады.
Бір айнымалы функцияның дифференциалдық есептеулері
Туынды үғымы - дифференциалдық есептеулерде ең негізгі ұғымдардың бірі болып санадады.
Анықтама.  функциясы
функциясы 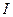 аралығында анықталсын. Егер
аралығында анықталсын. Егер 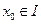 үшін
үшін
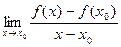
нақты мәнді шегі бар болса, онда  функциясын
функциясын  нүктесінде дифференциалданады, ал шектің мәнін
нүктесінде дифференциалданады, ал шектің мәнін  функциясының
функциясының  нүктесіндегі туындысы дейді де,
нүктесіндегі туындысы дейді де, 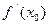 символымен белгілейді.
символымен белгілейді.
Сонымен, 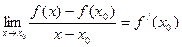
Туындының анықтамасын шекті белгілейтін символдарды қолданып келесідей жазуға болады:
1°. 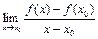 , 2°.
, 2°. 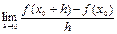 , 3°.
, 3°. 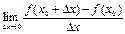 , 4°.
, 4°. 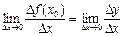 .
.
Соңғы екі жазуда 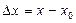 ,
, 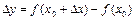 немесе
немесе 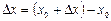 ,
, 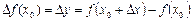 белгілеулері қолданылған.
белгілеулері қолданылған.
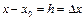 -ті функция аргументінің немесе тәуелсіз айнымалының өсімшесі, ал
-ті функция аргументінің немесе тәуелсіз айнымалының өсімшесі, ал 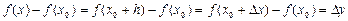 -ті функцияның өсімшесі деп атайды.
-ті функцияның өсімшесі деп атайды.
Туындының мынадай белгіленулері бар:
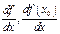 немесе
немесе 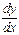 ,:
,: 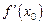 немесе
немесе 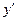 ,
, 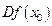 немесе
немесе 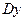
Бұл символдар былай оқылады: 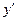 – игрек штрих,
– игрек штрих, 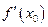 – эф штрих икс ноль,
– эф штрих икс ноль, 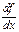 – дэ икс бойынша дэ эф,
– дэ икс бойынша дэ эф, 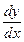 – дэ икс бойынша дэ игрек,
– дэ икс бойынша дэ игрек, 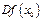 – дэ эф икс ноль;
– дэ эф икс ноль; 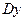 – дэ игрек.
– дэ игрек.
1-теорема. Егер 
 функциясының
функциясының  нүктесінде туындысы бар болса, онда
нүктесінде туындысы бар болса, онда  сол нүктеде үзіліссіз болады.
сол нүктеде үзіліссіз болады.
1-теоремаға кері теорема дұрыс емес: егер  функциясы
функциясы  нүктесінде үзіліссіз болса оның сол нүктеде туындысы әрқашанда бола бермейді. Демек, функция
нүктесінде үзіліссіз болса оның сол нүктеде туындысы әрқашанда бола бермейді. Демек, функция  нүктесінде үзіліссіз бола тұрып, ол нүктеде дифференциалдануы да, дифференциалданбауы да мүмкін.
нүктесінде үзіліссіз бола тұрып, ол нүктеде дифференциалдануы да, дифференциалданбауы да мүмкін.
Мысалы, 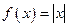 функциясының
функциясының 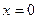 нүктесінде үзіліссіз, оң және сол жақты туындылары бар болады да, бірақ жай (екі жақты) туындысы болмайды.
нүктесінде үзіліссіз, оң және сол жақты туындылары бар болады да, бірақ жай (екі жақты) туындысы болмайды.
Салдар. Егер  нүктесі
нүктесі  функциясының үзіліс нүктесі болса, онда сол нүктеде
функциясының үзіліс нүктесі болса, онда сол нүктеде  – тің ақырлы туындысы болмайды.
– тің ақырлы туындысы болмайды.
2. Дифференциалдау ережелері
2-теорема. 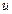 және
және 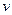 функциялары
функциялары 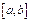 сегментінде анықталып,
сегментінде анықталып,  нүктесінде дифференциалдансын. Онда
нүктесінде дифференциалдансын. Онда 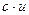 (
(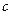 -нақты сан),
-нақты сан), 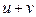 ,
, 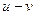 ,
, 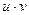 ,
, 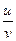 функциялары да
функциялары да 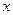 нүктесінде дифференциалданып, келесі теңдіктер (дифференциалдау ережелері) орындалады:
нүктесінде дифференциалданып, келесі теңдіктер (дифференциалдау ережелері) орындалады:
1. 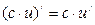 ; 2.
; 2. 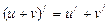 ; 3.
; 3. 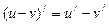 ; 4.
; 4. 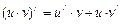 ;
;
5. 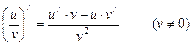 .
.
3. Күрделі, кері және параметр арқылы берілген функцияның туындысы
3-теорема (күрделі функцияның туындысы). Егер 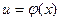 функциясының
функциясының  нүктесінде, ал
нүктесінде, ал 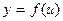 функциясының сол
функциясының сол  -ге сәйкес
-ге сәйкес 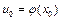 нүктесінде туындысы бар болса, онда
нүктесінде туындысы бар болса, онда 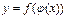 күрделі функциясының
күрделі функциясының  нүктесінде туындысы бар болып,
нүктесінде туындысы бар болып, 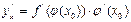 болады.
болады.
Күрделі функцияның туындысын, есте сақталуы өте жеңіл болатын
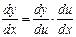 немесе
немесе 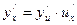
түрінде де жазуға болады.
4-теорема ( кері функцияның туындысы). Егер 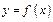 функциясы
функциясы 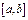 сегментінде үзіліссіз және қатаң монотонды болып,
сегментінде үзіліссіз және қатаң монотонды болып, 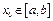 нүктесінде нөлге тең емес туындысы бар болса, онда
нүктесінде нөлге тең емес туындысы бар болса, онда 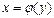 кері функциясының да
кері функциясының да 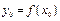 нүктесінде туындысы бар болып,
нүктесінде туындысы бар болып,
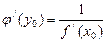 (4.3)
(4.3)
теңдігі орындалады.
(4.3) - формуланы 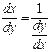 немесе
немесе 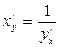 түрінде де жазады.
түрінде де жазады.
Параметр арқылы берілген функцияның туындысы
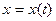 және
және 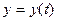 функциялары
функциялары 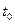 нүктесінің маңайында анықталып, олардың біреуінің, мысалы
нүктесінің маңайында анықталып, олардың біреуінің, мысалы 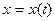 функциясының қарастырылып отырған маңайда кері функциясы
функциясының қарастырылып отырған маңайда кері функциясы 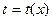 бар болсын. Онда күрделі
бар болсын. Онда күрделі 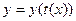 функциясын
функциясын 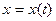 ,
, 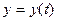 теңдеулерімен параметр арқылы берілген функция деп ал,
теңдеулерімен параметр арқылы берілген функция деп ал, 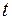 -ны параметр деп атайды.
-ны параметр деп атайды.
Мысалы, 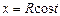 және
және 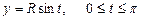 функциясы,
функциясы, 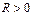 болғанда
болғанда 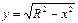 функциясының параметр арқылы берілуі.
функциясының параметр арқылы берілуі.
5-теорема. Егер 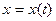 және
және 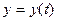 функцияларының
функцияларының 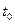 нүктесінде туындылары бар және
нүктесінде туындылары бар және 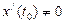 болса, ондапараметр арқылы берілген
болса, ондапараметр арқылы берілген 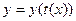 функциясының
функциясының 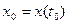 нүктесінде туындысы бар және
нүктесінде туындысы бар және
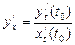 (4.6)
(4.6)
болады.
(4.6)- формуланы келесі түрде де жазуға болады: 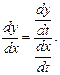
Мысалы, 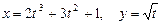 параметр арқылы берілген функцияның туындысын табайық.
параметр арқылы берілген функцияның туындысын табайық.
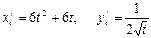 болғандықтан, (4.6)- формула бойынша
болғандықтан, (4.6)- формула бойынша 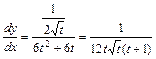 болады.
болады.
Гиперболалық функциялардың туындылары
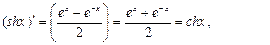
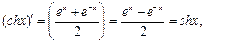
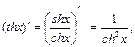
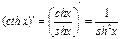 .
.
Дәрежелі-көрсеткіштік функцияның туындысы
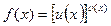 дәрежелі-көрсеткіштік функцияның туындысын табайық. Мұндағы,
дәрежелі-көрсеткіштік функцияның туындысын табайық. Мұндағы, 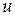 және
және 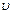 функцияларының
функцияларының 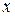 нүктесінде туындысы бар және
нүктесінде туындысы бар және 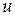 функциясы
функциясы 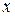 - тің белгілі бір маңайында оң деп ұйғарамыз.
- тің белгілі бір маңайында оң деп ұйғарамыз.
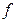 -ті анықтайтын өрнектің екі жағын да логарифмдесек
-ті анықтайтын өрнектің екі жағын да логарифмдесек 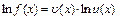 болады. Соңғы теңдіктің екі жағын да дифференциалдайық:
болады. Соңғы теңдіктің екі жағын да дифференциалдайық: 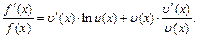
Бұдан 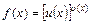 екенін ескере отырып,
екенін ескере отырып,
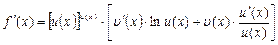 (4.10)
(4.10)
формуласына келеміз.
Мысалы, 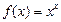
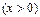 болсын. Онда
болсын. Онда 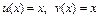 болады, демек, (4.10) бойынша
болады, демек, (4.10) бойынша 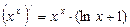 .
.
5. Функцияның дифференциалы
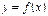 функциясының
функциясының 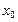 нүктесінде
нүктесінде 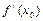 туындысы бар болсын. Онда, туындының анықтамасы бойынша
туындысы бар болсын. Онда, туындының анықтамасы бойынша
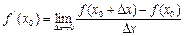 .
.
Шектің қасиеті бойынша келесі теңдікті аламыз:
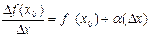 (4.11)
(4.11)
мұнда 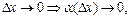
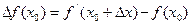 —
— 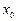 нүктесіндегі аргументтің өсімшесі
нүктесіндегі аргументтің өсімшесі 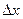 -ке сәкес функцияның өсімшесі.
-ке сәкес функцияның өсімшесі.
(4.11)-ден
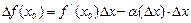 (4.12)
(4.12)
Сонымен, егер 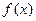 функциясының
функциясының 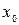 нүктесінде нөлге тең емес туындысы бар болса, онда функцияның сол нүктедегі өсімшесі екі қосылғыштан тұрады. (4.12) формуладағы бірініші қосылғыш
нүктесінде нөлге тең емес туындысы бар болса, онда функцияның сол нүктедегі өсімшесі екі қосылғыштан тұрады. (4.12) формуладағы бірініші қосылғыш 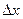 -ке қатысты сызықты және
-ке қатысты сызықты және 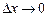 болғанда шексіз аз шама. Осы формуладағы екінші қосылғыш та
болғанда шексіз аз шама. Осы формуладағы екінші қосылғыш та 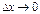 болғанда шексіз аз шама.
болғанда шексіз аз шама.
Анықтама. 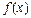 функциясының
функциясының 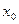 нүктесінде
нүктесінде 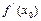 туындысы бар болса, онда
туындысы бар болса, онда 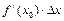 көбейтіндісін
көбейтіндісін 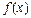 функциясының
функциясының 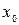 нүктесіндегі дифференциалы деп атап, оны
нүктесіндегі дифференциалы деп атап, оны 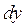 немесе
немесе 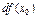 арқылы белгілейді.
арқылы белгілейді.
Сонымен, 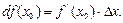
Тәуелсіз айнымалы х - тің өсімшесін 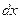 арқылы белгілеп, оны тәуелсіз айнымалының дифференциалы деп атайды. Дифференциалды
арқылы белгілеп, оны тәуелсіз айнымалының дифференциалы деп атайды. Дифференциалды
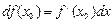 немесе
немесе 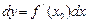
түрінде жазуға болады.
Функцияның нүктедегі дифференциалы, сол нүктеде туындысының бар болуымен байланысты.
Сонымен, дифференциал — 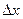 -ке қатысты сызықты функция, ал оның коэффициенті
-ке қатысты сызықты функция, ал оның коэффициенті  функциясының
функциясының 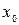 нүктесіндегі туындысы болады.
нүктесіндегі туындысы болады.
Мысалы, 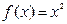 функциясының дифференциалы
функциясының дифференциалы 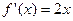 болғандықтан,
болғандықтан, 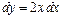 .
.
Дифференциал — туынды мен 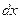 - тәуелсіз айнымалының көбейтіндісі болғандықтан, негізгі элементар функциялардың дифференциалдары мен дифференциалды табу ережелері туындылар үшін дәлелденген сәйкес формулалар мен ережелерден шығады.
- тәуелсіз айнымалының көбейтіндісі болғандықтан, негізгі элементар функциялардың дифференциалдары мен дифференциалды табу ережелері туындылар үшін дәлелденген сәйкес формулалар мен ережелерден шығады.
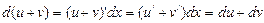 ,
, 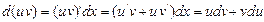
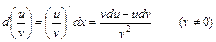 .
.
Функция дифференциалының функция өсімшесі 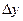 -тен айрмашылығы
-тен айрмашылығы 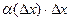 шамасына тең. Сондықтан, жуықтап есептеулерде
шамасына тең. Сондықтан, жуықтап есептеулерде 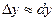 жуық теңдігін пайдаланады. Осыдан
жуық теңдігін пайдаланады. Осыдан
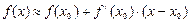 (4.13)
(4.13)
Мысалы, 
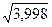 есептеу үшін
есептеу үшін 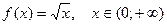 функциясын қарастырамыз. Осы функция үшін (4.13) формула келесідей болады:
функциясын қарастырамыз. Осы функция үшін (4.13) формула келесідей болады:
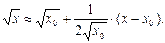
Осы формулаға 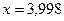 және
және 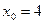 мәндерін қойсақ, онда
мәндерін қойсақ, онда
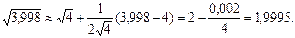
Мысалдар. 1. 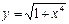 функциясының туындысын табыңыз.
функциясының туындысын табыңыз.
Шешуі. 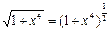 болғандықтан,
болғандықтан, 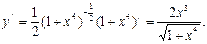
2. 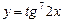 функциясының туындысын табыңыз.
функциясының туындысын табыңыз.
Шешуі. 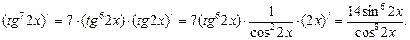
3. 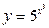 функциясының туындысын табыңыз.
функциясының туындысын табыңыз.
Шешуі. 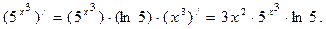
4. 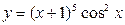 функциясының туындысын табыңыз.
функциясының туындысын табыңыз.
Шешуі. Көбейтіндінің туындысы мен күрделі функцияның туындысын табу ережелерін қолданамыз (4.2 және 4.3-теоремалар). Сонда,
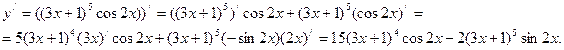
6. Жоғары ретті туындылар
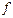 функциясы
функциясы 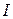 аралығында дифференциалдансын. Онда әрбір
аралығында дифференциалдансын. Онда әрбір 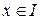 санына
санына 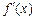 нақты санын сәйкес қоятын ереже функция болады. Ол
нақты санын сәйкес қоятын ереже функция болады. Ол 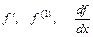 немесе
немесе 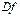 символдарымен белгіленеді. Әрине,
символдарымен белгіленеді. Әрине, 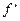 функциясының
функциясының 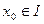 нүктесінде туындысы бар болуы туралы сұрақ қоюға болады (келісім бойынша «туынды» деген сөзді «ақырлы туынды» мағынасында түсіну керек екенін еске саламыз).
нүктесінде туындысы бар болуы туралы сұрақ қоюға болады (келісім бойынша «туынды» деген сөзді «ақырлы туынды» мағынасында түсіну керек екенін еске саламыз).
Егер 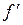 функциясы
функциясы 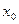 нүктесінде дифференциалданса, яғни
нүктесінде дифференциалданса, яғни 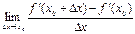 нақты мәнді шегі бар болса, онда сол шекті
нақты мәнді шегі бар болса, онда сол шекті 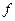 функциясының
функциясының 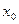 нүктесіндегі екінші ретті туындысы деп атайды да,
нүктесіндегі екінші ретті туындысы деп атайды да, 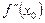 символымен белгілейді.
символымен белгілейді.
Егер 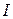 аралығының әрбір нүктесінде
аралығының әрбір нүктесінде 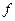 функциясының екінші ретті туындысы бар болса, онда
функциясының екінші ретті туындысы бар болса, онда 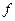 функциясы
функциясы 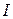 аралығында екі рет дифференциалданады немесе екінші ретті туындысы бар дейді.
аралығында екі рет дифференциалданады немесе екінші ретті туындысы бар дейді.
Индукция бойынша бұл анықтамалар кез келген оң бүтін 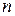 жағдайына таратылады:
жағдайына таратылады:
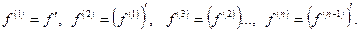
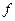 функциясын
функциясын 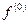 символымен белгілеген кейде ыңғайлы болады.
символымен белгілеген кейде ыңғайлы болады.
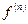 функциясын
функциясын 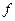 функциясының
функциясының 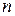 -ші ретті туындысы деп атайды.
-ші ретті туындысы деп атайды.
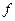 функциясының
функциясының 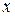 нүктесіндегі
нүктесіндегі 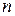 ретті туындысы
ретті туындысы
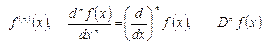
символдарының бірімен белгіленеді (оқылуы сәйкес «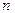 -ші эф икс», «дэ эн икс бойынша дэ эн эф», «дэ эн эф икс»).
-ші эф икс», «дэ эн икс бойынша дэ эн эф», «дэ эн эф икс»).
Кейде бұл символарды 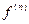 функциясының өзін де белгілеу үшін қолданады.
функциясының өзін де белгілеу үшін қолданады.
Екінші ретті туындының механикалық мағынасын атап өтейік.
Егер нүктенің қозғалысы 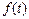 функциясымен бейнеленсе, онда
функциясымен бейнеленсе, онда 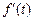 сол нүк те қозғалысының «жылдамдығын» бейнелейді. Ал,
сол нүк те қозғалысының «жылдамдығын» бейнелейді. Ал, 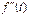 қарастырылып отырылған нүкте қозғалысының «жылдамдығының жылдамдығын», яғни қозғалыстың үдеуін бейнелейді.
қарастырылып отырылған нүкте қозғалысының «жылдамдығының жылдамдығын», яғни қозғалыстың үдеуін бейнелейді.
 2015-09-06
2015-09-06 1792
1792








