К конкретным молекулам

Наглядную иллюстрацию групповых правил можно продемонстрировать на примере молекулы, которая принадлежит к точечной группе симметрии С _3u, включающей следующие операции симметрии: I (идентичная операция). 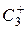(поворот молекулы на 120° вокруг оси Z по часовой стрелке), 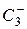(тот же поворот на 120° против часовой стрелки), 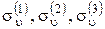– плоскости отражения, проходящие через атом N и соответствующие атомы водорода Н₁, Н₂, Н₃ (см. рис. 4.6). Возможны и другие операции симметрии, но все они будут эквивалентны какой-либо из приведенных. Например, поворот молекулы по часовой стрелке вокруг оси Z на 240° (т. е. 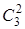) равносилен операции 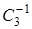(повороту на 120° против часовой стрелки). Можно также показать, что последовательное повторение какой-либо из этих операций эквивалентно некоторой однократной операции из рассмотренной группы. применим к данной молекуле операцию 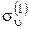.Это приведет к обмену местами атомов водорода Н₂ и Н₃. Если к полученной при этом конфигурации применим операцию С ₃⁺, то окончательная конфигурация будет такой же, что и в случае однократного применения операции 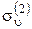к исходной конфигурации. По групповым законам это можно записать так: 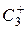× 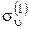= 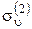(т. е. произведение одной операции симметрии на вторую дает новую операцию симметрии из той же группы, а произведение двух элементов группы дает третий элемент, принадлежащий группе). Если рассмотреть все возможные комбинации умножения, то получится табл. 4.2, в которой операции, примененные первыми, записаны в первой строке таблицы.

Таблица 4.2

Таблица произведений точечной группы симметрии С _3u

	I	C 3	С 3-1	su(1)	su(2)	su(3)
I	I	C 3	С 3-1	su(1)	su(2)	su(3)
C 3	C 3	С 3-1	I	su(3)	su(1)	su(2)
С 3-1	С3-1	I	C3	su(2)	su(3)	su(1)
su(1)	su(1)	su(2)	su(3)	I	C 3	С3 -1
su(2)	su(2)	su(3)	su(1)	С 3-1	I	C3
su(3)	su(3)	su(1)	su(2)	C 3	С 3-1	I

Согласно таблице можно найти, что произведение двух любых элементов будет давать третий элемент группы, который находится на пересечении строки и столбца. Такая таблица называется таблицей произведений группы.

Пользуясь этой таблицей, можно проверить все групповые правила, сформулированные в п. 4.1, т. е. последовательное выполнение двух операций дает третью операцию, принадлежащую группе, совокупность содержит единичный элемент. для всех элементов выполняется правило ассоциативности. каждый элемент имеет себе обратный. например, операции С ₃ обратная операция 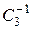, которая уничтожает действие первой, т. е. 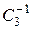× С ₃ = I.

Следует отметить, что коммутативный закон для произведений не обязательно выполняется, т. е. окончательный результат действия двух операций, вообще говоря, зависит от порядкаих следования (проверить это предоставляем читателю).

Для молекулы типа аммиака NH₃ все шесть элементов симметрии можно разбить на три типа операций: операция идентичности I, поворота С₃ и отражения s_u. Каждый из этих типов образует класс. Таким образом, шесть операций симметрии молекулы NH₃ разбиваются на три класса (I, 2 С ₃, 3s_u). В молекуле воды (С _2u) четыре операции симметрии образуют 4 класса (т. е. один элемент симметрии образует класс). Согласно групповым законам две операции образуют один класс, если одну из них можно получить из другой некоторым преобразованием координат, состоящимиз элементов симметрии данной точечной группы. Указанные операции эквивалентны в том смысле, что взаимно заменяют друг друга при различном выборе системы координат. Свойство волновой функции или колебательной координаты быть симметричной или антисимметричной по отношению к определенной операции симметрии одинаково для всех операций, принадлежащих одному классу. Для сокращения все шесть элементов точечной группы С _3u обозначают так: I, 2 С ₃, 3s_u (табл. 4.3).

Соотношение между элементами точечной группы С _3u неудобно для пользования в силу своей громоздкости. Поэтому на практике стараются упростить таблицу, заменив ее элементы некоторой матрицей или просто числом, лишь бы они воспроизводили таблицу произведений (т. е. полностью удовлетворяли групповым законам). Любой набор таких выражений, который удовлетворяет соотношениям, даваемым таблицей произведений, называется представлением группы (Г). Представления бывают приводимые и неприводимые. Одно из возможных представлений группы С _3u, приведено в табл. 4.3. Легко проверить, что каждое представление в этой таблице удовлетворяет таблице произведений.

Таблица 4.3

Одно из возможных представлений группы С_3u

С 3u	I	С3	С3–1	su(1)	su(2)	su(3)
Г 1(А 1)	I	I	I	I	I	I
Г 2(А 2)	I	I	I	–I	–I	–I
Г 3(Е)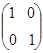

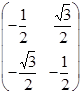
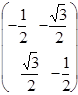
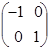
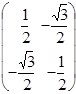
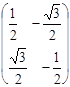
Г ₁ и Г ₂ дают невырожденное представление, а Г ₃ – дважды вырожденное.

для точечной группы С _3u можно привести ряд других представлений, которые будут удовлетворять соотношениям, даваемым таблицей произведений.

Пример в табл. 4.3 показывает, что полное представление группы Г можно разбить на более простые представления: Г ₁, Г ₂, Г ₃. Итак, для группы С _3u существуют только три неприводимых представления. Для группы С _2u существуют четыре неприводимых представления. Точечные группы, а также нормальные колебания молекулы делятся на типы симметрии в соответствии с их неприводимыми представлениями. Число неприводимых представлений точечной группы симметрии равно числу классов. Например, для группы С _3u число типов симметрии равно трем, а для С _2u – четырем.

В приложении теории групп для колебаний молекул и в электронной спектроскопии проще иметь дело не с самими матрицами представлений, а с их характерами. Под характером матрицы подразумевают сумму диагональных элементов. Как видно из табл. 4.3, характер матрицы всех элементов преобразований, относящихся к одному классу, одинаков. Пользуясь следами матриц представлений точечной группы С _3u, можно существенно упростить и получить таблицу характеров точечной группы С _3u (табл. 4.4).

Для всех существующих точечных групп симметрии составлены свои таблицы характеров, которые приводятся во всех руководствах по молекулярной спектроскопии. В дальнейшем будем пользоваться исключительно таблицей характеров, а не соответствующими матрицами представлений.

Таблица 4.4

Таблица характеров представлений точечной группы С _3u

С 3u	I	2 С 3u	3su
Г 1(А 1)
Г 2(А 2)			–1
Г 3(Е)		–1

4.8. Представления группы симметрии.
Линейные преобразования координат,
соответствующие операциям симметрии

При изучении операций симметрии (поворотов, отражений и др.) иногда полезно знать матрицы, описывающие указанные операции. Пусть мы имеем n функций от декартовых координат y₁(x, y, z), y₂(x, y, z), y₃(x, y, z)..., y _n (x, y, z) и подвергаем одну из них, скажем y _k (x, y, z), преобразованию симметрии R. получим новую функцию y '_k, которую легко выразить через старые функции y _k в виде их линейных комбинаций:

y' _k = C_{k 1}y₁ + C_k2 y₂ +... + C_kn y _n (4.47)

или .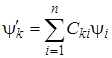

Из коэффициентов преобразования C_ki можно составить квадратную матрицу

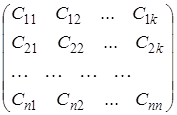. (4.48)

Возьмем второй пример. Пусть заданы координаты точки Р(x,y,z) в системе декартовых координат(рис. 4.12). Для простоты считаем, что х = 1, у = 1 и z = 1. Рассмотрим,как изменяются координаты точки под действием различных операций симметрии. Произведем операцию отражения этой точки в плоскости ХОУ, т. е. точка Р перейдет в точку Р', а координаты ее изменятся на (х, у, –z) Следовательно, результат операции отражения в плоскости ХОУ можно записать следующим образом:

x' = x, y' = y, z' = –z. (4.49)

Эту операцию можно описать с помощью умножения матриц:

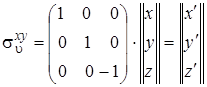. (4.50)

выполнив умножение квадратной матрицы слева на матрицу столбец, получим: х' = х, у' = у, z' = –z, что соответствует (4.49). Говорят, что квадратная матрица (4.50) является представлением операции отражения в плоскости XOY. Тождественное преобразование над точкой Р приводит к новой системе координат, которая ничем не будет отличаться от старой. Эту операцию можно описать с помощью умножения матриц

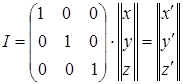. (4.51)

Выполнив умножение квадратной матрицы слева на матрицу столбец, получим х = х', у = у', z =z'. В этом случае говорят, что мы над точкой провели тождественное преобразование. Этому преобразованию соответствует единичная матрица.

Аналогично можно записать, что результат отражения точки Р в плоскости YOZ (операция s_u^{( y,z )} ) будет выражаться в матричном виде следующим образом:

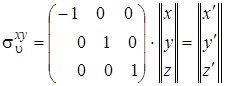.(4.52)

после перемножения получим x' = –x, y' = y, z' = z.

При операции инверсии i знаки координат точки Р изменяются на обратные. В матричной записи это будет представляться так:

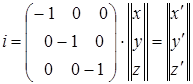, (4.53)

(т. е. х' = –х, у' = –y, у, z' = –z).

В аналитической геометрии показано, что при переходе от одной системы координат (x, y, z) к другой системе координат (x', y', z'), повернутой относительно первой на угол j против часовой стрелки (поворот осуществляется вокруг оси Z), новые координаты выражаются через старые посредством следующих соотношений:

x' = x cos j + y sinj) + 0× z,

y' = – x sinj + y cosj + 0× z, (4.54)

z ' = x ×0 + y ×0 + 1× z,

В матричной записи это будет выглядеть следующим образом:

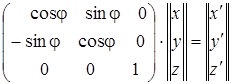, (4.55)

где матрица преобразования от одной системы координат к другой будет выглядеть как

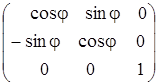, (4.56)

след которой будет равен 1 + 2cosj (сумма диагональных элементов). Следовательно, операции поворота C_n на угол j = 2p/ n будет соответствовать матрица

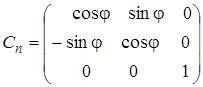. (4.57)

Легко показать, что зеркально-поворотной операции S_n б удет соответствовать матрица

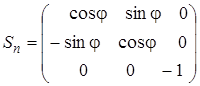. (4.58)

Из рассмотрения квадратных матриц, записанных выше, следует, что если в результате преобразования координата х не преобразуется ни в у, ни в z, то в соответствующей строке матрицы преобразования будут стоять нули, а ненулевое значение будет иметь только диагональный член (для х – это первый элемент 1-й строки, для у – 2-й элемент 2-й строки, для z – 3-й элемент 3-й строки). Недиагональные матричные элементы возникают в тех случаях, когда в результате преобразования координаты одного типа выражаются через другие, как это было при рассмотрении поворота системы координат на угол j против часовой стрелки. Таким образом, видим, что операции симметрии можно представлять с помощью квадратных ортогональных матриц, которые подчиняются правилам группового умножения.

С другой стороны, полученные преобразования координат для различных операций позволяют понять некоторые следствия из групповых законов

1) 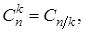если k = n /2, то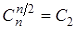

2) 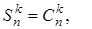если k четное

3)

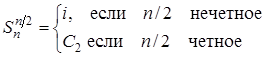
4)

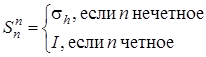
С помощью умножения матриц легко показать, что выполняются следующие соотношения:

1) ,

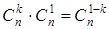2) ,

3) ,

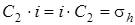4) ,

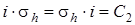5) .

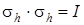В качестве примера далее рассмотрим все матрицы преобразования, которые соответствуют точечной группе симметрии С _3u (молекула NH₃ см. рис. 4.6). Примем, что осью симметрии С ₃ является ось z, а ось х расположена в плоскости s_u^{( 1 )}. Точечная группа симметрии С _3u состоит из 6 элементов (операций), каждому из которых можно сопоставить квадратную матрицу следующего вида:

, ,

,

,, .

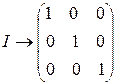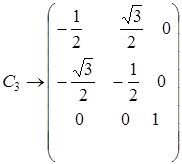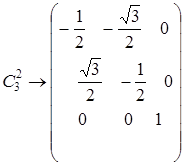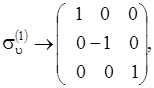
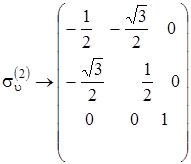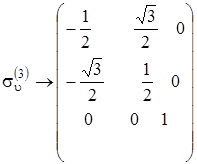Замечательным свойством этих матриц является то, что они будут копировать (повторять) таблицу группового умножения. Например

= ,

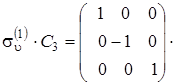
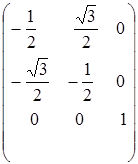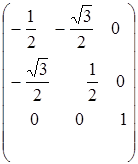что соответствует операции 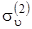, т. е. произведение операции С ₃ на операцию 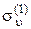дает новую операцию, принадлежащую группе.

Таким образом, вместо группы симметрии молекулы вводят эквивалентную ей группу матриц, элементами которой являются более удобные для математического описания объекты (числа).

Итак, всякую совокупность матриц, которые подчиняются таблице группового умножения, называют представлением группы. Другими словами, представление группы – это набор матриц, который показывает, как при операциях группы симметрии преобразуются координаты точки. Матрицы описывают группу на языке матричного исчисления.

В рассмотренном примере молекулы NH₃ представление ее точечной группы можно выполнить с помощью двумерных матриц, которые получим, если вычеркнем в трехмерных матрицах каждые строку и столбец. После этого получим:

, , ,

, , .

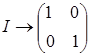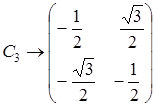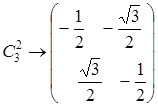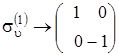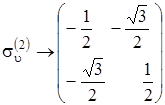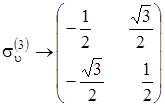Это одно из представлений группы C _3uс помощью матриц более низкой размерности.

Каждая группа симметрии может иметь бесчисленное множество представлений, которые могут отличаться друг от друга как размерностью своих матриц, так и видом матричных элементов. Иногда вместо матриц могут выступать просто наборы чисел (число можно рассматривать как квадратную матрицу единичной размерности). Среди большого числа представлений группы существуют так называемые неприводимые представления. В теории групп разработаны определенные правила, позволяющие переходить от одного набора квадратных матриц к другому. Иногда можно подобрать такое преобразование, которое приводит к более простым матрицам, обладающим меньшей размерностью, чем исходные. Если можно упростить матрицы данного представления путем соответствующего алгебраического преобразования, то о таком представлении говорят как о приводимом. Если же нельзя подобрать никакого преобразования, упрощающего вид исходных матриц, то говорят, что данное представление неприводимо.

Известно, что при подходящем выборе системы координат матрицу каждого преобразования можно привести к диагональной форме (иногда к блок-диагональной форме). Это позволяет полное представление группы Г привести к сумме неприводимых представлений Г ⁽¹⁾, Г ⁽²⁾,... Г ^{( k )} (см. табл. 4.3). Это приведение осуществляется при помощи некоторого преобразования координат, которое оставляет характер матрицы неизменным. Такие преобразования называют преобразованиями подобия. Поэтому характер матрицы приводимого представления c(R) записывается в виде суммы

c(R) = n⁽¹⁾ c⁽¹⁾(R) + n⁽²⁾ c⁽²⁾ (R) +...+ n^(k) c^(k)(R) = 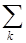n^(k) c^(k)(R), (4.59)

где c^{( k )}(R) – характер соответствующего неприводимого представления, коэффициенты n ⁽¹⁾, n ⁽²⁾,..., n ^{( k )} показывают, сколько раз данное неприводимое представление Г ^{( k )} содержится в данном приводимом Г. Сумма в формуле (4.59) берется по всем операциям симметрии в группе.

В теории групп показано, что для любой таблицы характеров выполняется так называемое соотношение ортогональности, т. е.

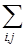c _i (R) c _j (R) = h d _ij, (4.60)

где d _ij – символ Кронекера (он равен 0 при i ¹ j и 1 при i = j), h – порядок группы (он равен числу имеющихся элементов симметрии). Учитывая это свойство, и умножая равенство 4.59 слева и справа на c _i (R), и суммируя по всем операциям группы, мы получим

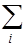c^{( i)} (R) c _i (R) = n ^{( i )} h. (4.61)

(Значок < аналогично k пробегает все значения по числу операций симметрии). Из выражения (4.61) получим, что

n ^{( i )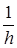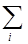} = c^{( i)} (R) c _i (R). (4.62)

Если в группе имеются классы, a g есть число элементов в классе, то формулу можно переписать следующим образом:

n ^{( i )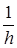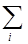} = g _i c^{( i )} (R) c _i (R), (4.63)

где c^{( i )}(R) – характер полного приводимого представления в данном i -ом классе; g_i – число элементов в i -ом классе; c _i (R) – характер неприводимого представления (дается в таблице характеров для i -го класса).

Учитывая, что число типов симметрии данной точечной группы равно числу классов, для подсчета числа колебаний n ^{( i )} данного типа симметрии заданной молекулы можно пользоваться формулой (4.63). Для отнесения колебаний по типам симметрии и подсчета числа таких колебаний рассмотрим предварительно, как вводятся в молекуле новые координаты для характеристики колебательного движения.