Пример 6. 6

Супруги X и Y ранжировали 8 жизненных ценностей по степени предпочтения. Данные представлены в таблице:

Ценности	Ранги X	Ранги Y	Р (совпадения)	Q (инверсии)
Здоровье
Любовь
Богатство
Свобода
Мудрость
Познание
Развитие
Творчество
			2 = 20

В качестве меры согласованности предпочтений супругов вычислим корреляцию т₄-Кендалла, так как наблюдаются связи в рангах: одна группа из трех рангов по Хи две группы по три ранга по Y.

Обратите внимание на подсчет совпадений для объектов, попадающих в «связки». Например, для объекта «Богатство» пропускаются два ниже находящихся объекта, как имеющие одинаковые с ним ранги по X.

КОРРЕЛЯЦИЯ БИНАРНЫХ ДАННЫХ

Как отмечалось ранее, если одна из двух переменных представлена в но­минативной шкале, а другая — в числовой (ранговой или метрической), то связь между этими переменными лучше изучать путем сравнения групп по уровню выраженности числовой переменной.

ПРИМЕР _________________________________________________

Предположим, исследуется связь количества пропущенных лекций студентами и курса обучения (с 1-го по 5-й). Первая переменная — метрическая, а вторая — но­минативная. Связь между этими переменными может быть изучена путем сравне­ния разных курсов по количеству пропущенных лекций (по средним значениям). Если будут обнаружены различия между курсами, то посещаемость лекций связана с курсом обучения, в противном случае — связи нет.

То же касается проблемы изучения связи между двумя номинативными переменными. Хотя и для этого случая существуют коэффициенты корреля­ции (К— Чупрова, С — Пирсона), но возможность их интерпретации весьма ограничена, в частности потому, что они отражают лишь силу связи, но не ее направление. Поэтому и в этом случае проблему связи между двумя номина­тивными переменными лучше изучать путем сравнения градаций одной пе­ременной по распределению другой переменной.

ПРИМЕР

Предположим, исследуется связь агрессивности учащихся (три градации: низкая, средняя, высокая) и образования их родителей (среднее, высшее техническое, выс­шее гуманитарное). Результаты исследования связей двух номинативных перемен­ных обычно представляются в виде таблицы сопряженности:

Агрессивность	Образование родителей
Среднее	Высш. технич.	Высш. гуманит.
Низкая
Средняя
Высокая

ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ

Связь между этими переменными может быть изучена путем сравнения распреде­лений учащихся по степени агрессивности для разных градаций образования роди­телей (или, что то же самое, путем сравнения распределения образования родите­лей для разных градаций степени агрессивности учащихся).

Исключением можно считать случай изучения связи двух бинарных перемен­ных. Бинарная переменная имеет только две градации, обычно обозначаемые как О и 1. Примеры таких переменных: пол (мужской, женский), образование (сред­нее, высшее), тревожность (низкая, высокая), успешность (низкая, высокая) и т. д. При изучении связей между бинарными переменными обычно строят че-тырехклеточные таблицы сопряженности:

Таблица 6.1 Таблица сопряженности 2x2

	Признак X	Итог
Признак Y		а	Ъ	а+ b
	с	d	с + d
Итог		а + с	b + d	N

В этом случае допустимо применение г-Пирсона (формула 6.1) непосред­ственно к исходным данным — двум бинарным переменным, принимающим значение 0 или 1, измеренным для каждого члена выборки численностью Л'. Результат применения r-Пирсона к двум бинарным переменным называется «фи-коэффициентом сопряженности» (Phi). Если данные представлены в четырех-клеточной таблице сопряженности, то применяется формула, существенно упрощающая расчеты, но дающая аналогичный результат:

ad-bc _c

ср = ■ , (6.10)

J(a + b)(c + d)(a + c)(b + d) где а, Ь, с, d соответствуют обозначениям в четырехклеточной таблице 6.1.

ПРИМЕР 6.7___________________________________________________________

Исследовалась связь семейного положения студенток (X: 0 — холостая, 1 — заму­жем) и их академической успеваемости (Y: 0 — закончила вуз, 1 — отчислена). В рас­поряжении исследователя есть данные для 12 студенток:

№

X

Y

Таблица сопряженности для этих данных:

	X	Итог
Y
Итог

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

Вычислим ф-коэффициент сопряженности:

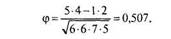Получена умеренная положительная взаимосвязь: холостые студентки чаше закан­чивают вуз, а замужние — чаще отчисляются. Отметим, что тот же самый результат был бы получен при применении формулы /'-Пирсона непосредственно к исход­ным данным.

Итак, ф-коэффициент есть просто /"-Пирсона, вычисленный для бинар­ных данных, а формула 6.10 алгебраически эквивалентна формуле 6.1. Следо­вательно, интерпретация ф-коэффициента подобна интерпретации /--Пирсо­на. Но использование ф-коэффициента существенно ограничено. Чем больше асимметрия распределения 0 и 1 по каждой переменной, тем менее точно ф-коэффициент отражает связь между бинарными переменными. Иначе го­воря, применение q-коэффициента требует приблизительного равенства коли­чества 0 и 1 по каждой переменной.

ВЕЛИЧИНА КОРРЕЛЯЦИИ И СИЛА СВЯЗИ

Коэффициенты корреляции были специально разработаны для численно­го определения силы и направления связи между двумя свойствами, измерен­ными в числовых шкалах (метрических или ранговых). Как уже упоминалось, максимальной силе связи соответствуют значения корреляции +1 (строгая прямая или прямо пропорциональная связь) и —1 (строгая обратная или об­ратно пропорциональная связь), отсутствию связи соответствует корреляция, равная нулю. Дополнительную информацию о силе связи дает значение ко­эффициента детерминации г²: это часть дисперсии одной переменной, кото­рая может быть объяснена влиянием другой переменной.

Однако в ряде случаев разные коэффициенты корреляции имеют различную эффективность, а иногда все они оказываются нечувствительными к связям.

Выбросы и отклонения распределений от нормальности

Выбросы — это экстремально большие или малые значения признака. В наибо­лее существенной степени выбросы вли­яют на корреляцию г-Пирсона, так как величина этого коэффициента прямо пропорциональна отклонению значения переменной от среднего.

ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ

ПРИМЕР 6.8

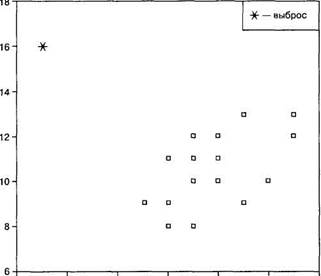
Воспользуемся данными из примера 6.1 с показателями вербального и невербаль­ного интеллекта, измеренного у 20 учащихся 8-го класса (г- 0,517). Добавим еще одно наблюдение: x₂₁ = 3,y₂i = 16 (см. рис. 6.5). Новое значение г-Пирсона для всех N= 21 теперь будет равно г— —0,124.

о.

ш

6 8 10

Вербальный IQ

Рис. 6.5. Демонстрация влияния экстремальных значений признаков («выброса») на коэффициент корреляции Пирсона

Пример 6.8 демонстрирует, что даже одно наблюдение с экстремально боль­шими или малыми значениями переменных может изменить знак корреля­ции на противоположный. Точно так же немногочисленные выбросы могут обусловить и появление корреляции.

Существенно меньшему влиянию выбросов подвержены ранговые корре­ляции. Поэтому один из способов борьбы с выбросами — переход к рангам и применение ранговых коэффициентов корреляции.

Для примера 6.8 ранговые коэффициенты корреляции (Спирмена и Кендалла) для первых 20 испытуемых (без выброса) составляют, соответственно: r_s = 0,505; х = 0,390. При добавлении выбросов: r_s = 0,294; т = 0,239. Значения корреляций уменьшилось, но не столь существенно, как л-Пирсона.

Другой подход к выбросам подразумевает «чистку» данных. Можно для каждой переменной установить определенное ограничение на диапазон ее изменчивости. Например, исключать те наблюдения, которые выходят за пре­делы диапазона М±2а (или даже М± 1,5а).

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

Часто такая «чистка» совершенно необходима. Например, при исследовании вре­мени реакции, когда основная масса наблюдений находится в диапазоне 250-700 мс, исключение нескольких «странных» значений меньше 50 мс и больше 1000 мс мо­жет существенно изменить общую картину.

По сути, наличие выбросов означает отклонение распределений одной или обеих переменных от нормального вида. В общем случае, если распределения переменных сильно скошены (асимметричны), это может существенно сни­жать значение корреляции даже при сильной связи между соответствующими свойствами или, наоборот, обусловить появление «ложной» корреляции. Осо­бенно сильно асимметричность распределений влияет на г-Пирсона. Поэто­му при существенном отклонении формы распределения хотя бы одной пере­менной от нормального вида желательно перейти к рангам и воспользоваться ранговым коэффициентом корреляции.

Влияние «третьей» переменной

Иногда корреляция между двумя переменными обусловлена не связью между соответствующими свойствами, а влиянием некоторой общей причи­ны совместной изменчивости этих переменных, которая зачастую выпадает из поля зрения исследователя. Эта общая причина может быть измерена как некоторая «третья» переменная, представленная либо в номинативной шка­ле, либо в количественной (ранговой или метрической) шкале.

Если истинная причина корреляции представляет собой номинативную пе­ременную, то это проявляется в характерной неоднородности выборки: в ней можно обнаружить различные группы, для которых согласованно меняются средние двух переменных, в то время как внутри групп эти переменные не кор­релируют. Если подобное явление возможно и существует способ содержательно интерпретируемого деления выборки на группы, необходимо вычислить кор­реляцию не только для всей выборки, но и для каждой группы в отдельности.

ПРИМЕР_______________________________________________________

Если мы возьмем достаточно большую группу людей — мужчин и женщин, то об­наружим существенную отрицательную корреляцию роста и длины волос: чем боль­ше рост, тем короче волосы. Однако, рассматривая график рассеивания роста и длины волос с выделением групп мужчин и женщин, мы обнаружим истинную при­чину этой корреляции — пол (рис. 6.6). Корреляции роста и длины волос отдельно для мужчин и отдельно для женщин будут близки к нулю.

Другой случай «ложной» корреляции — когда «третья» переменная может быть представлена в числовой шкале.

ПРИМЕР_______________________________________________________

Число церквей и количество увеселительных заведений в городах, как известно, сильно коррелируют, так же, впрочем, как рост и навык чтения у детей. Нетрудно

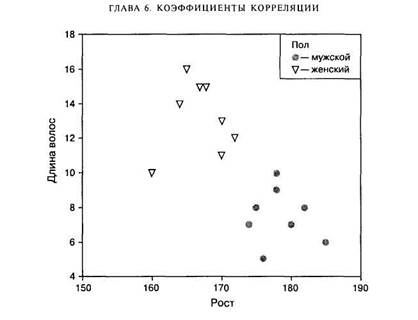
Рис. 6.6. График рассеивания для роста и длины волос. Темные точки — мужчины, светлые треугольники — женщины

догадаться, что в первом случае «третьей» переменной является численность го­родского населения, а во втором — возраст детей. (См. также пример 6.3 из раздела «Частная корреляция».)

Если истинная причина корреляции между двумя переменными Хп Y Из­мерена как количественная переменная Z, то предположение о том, что имен­но она является причиной корреляции, можно проверить, вычислив частную корреляцию r_xy__z по формуле 6.5. Если частная корреляция Хп Ус учетом Z (^rxy-_z) существенно меньше г^, то весьма вероятно, что именно Zявляeтcя ис­тинной причиной корреляции Хп Y.

Следует отметить, что за редким исключением факт наличия или отсутствия корреляции может быть объяснен влиянием некоторой «третьей» переменной, упущенной из поля зрения исследователя. Таким образом, всегда остается воз­можность альтернативной интерпретации обнаруженной корреляции.

\

Нелинейные связи

Еще одним источником низкой эффективности корреляций являются воз­можный нелинейный характер связи между переменными. То, какой характер имеет связь между переменными, можно заметить, рассматривая график дву­мерного рассеивания. Это свидетельствует о важности визуального анализа свя­зи с помощью таких графиков во всех случаях применения корреляций.

К отклонениям от прямолинейной зависимости любого рода наиболее чув­ствителен коэффициент корреляции r-Пирсона. Однако если нелинейная

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

связь оказывается монотонной, то возможен переход к рангам и применение ранговых корреляций.

Довольно часто в исследованиях встречаются немонотонные связи — ког­да связь меняет свое направление (с прямого на обратное, или наоборот) при увеличении или уменьшении значений одной из переменной.