Факультет технологии и исследования материалов

Кафедра исследования структуры и свойств материалов

Отчет

о лабораторной работе

«Статистическое моделирование»

Выполнил студент гр. 4064/2 Владимиров А. Д.

Преподаватель Вяххи И. Э.

Санкт-Петербург

1. Цель работы

Изучение стадий построения статистической модели и разработка такой модели на основе экспериментальных данных.

2. Теоретическое обоснование

Статистические модели выполняют функции «черного ящика», т.е. они используют связь между входными и выходными характеристиками системы для того, чтобы, не зная механизмов, проходящих в системе, иметь возможность предсказывать поведение системы. Применение статистических моделей целесообразно в следующих случаях:

1). Когда на систему оказывается значительное воздействие случайных факторов со стороны окружающей среды или из-за процессов внутри самой системы, т.е. выходные параметры начинают испытывать колебания, на фоне которых сложно выявить детерминированное поведение системы. В таком случае статистическая модель представляет собой аппарат для осреднения выходных значений, прогнозирования поведения системы на фоне значительных случайных колебаний данных.

2). Когда процессы, происходящие в системе, могут быть детерминированы, т.е. их механизм определяем, но данное описание сложно математически, трудоемко, требует большого количества экспериментов для определения параметров (выходных переменных) модели. В данной ситуации использование статистической модели проще, экономичнее, а также оно позволяет получить достаточно точные данные, базируясь только на результатах экспериментов.

Построение и исследование статистической модели включает разработку, оценку качества и исследование поведения системы уравнений, описывающих некоторый процесс. Исходная информация добывается путем проведения специального эксперимента с реальной системой, для чего созданы методы подготовки (планирования) таких экспериментов и обработки их результатов, а также критерии оценки полученных моделей.

Для экономии количества экспериментов необходимо одновременно изменять все факторы по определенному плану, это называется многофакторным планируемым экспериментом (МПЭ). План проведения МПЭ разрабатывается так, чтобы устранить корреляцию между факторами, для чего используют ортогональное планирование эксперимента. Для извлечения наибольшей информации из проводимых экспериментов и снижения ошибки модели расположение экспериментов в факторном пространстве должно быть равномерным и равноудаленным относительно центра экспериментов.

При разработке статистической модели ограничиваются обычно варьирование факторов на двух уровнях. Для проведения полного факторного эксперимента (ПФЭ) при k факторах осуществляют N=2^k опытов со всевозможными сочетаниями двух (х_i= +1 и x_i= -1) уровней факторов. Но уже при k=5 получается избыточное количество экспериментов: N=2⁵=32, поэтому используют дробно-факторный эксперимент (ДФЭ), для которого число экспериментов N=2^k-p, где р – мера дробности. Для построения матрицы ДФЭ в качестве базы используют ПФЭ для k-p факторов, а недостающие столбцы формируют на основе генерирующего соотношения вида x_k=x_i·x_j c использованием известных значений факторов в i и j столбцах.

Этапы построения статистической модели:

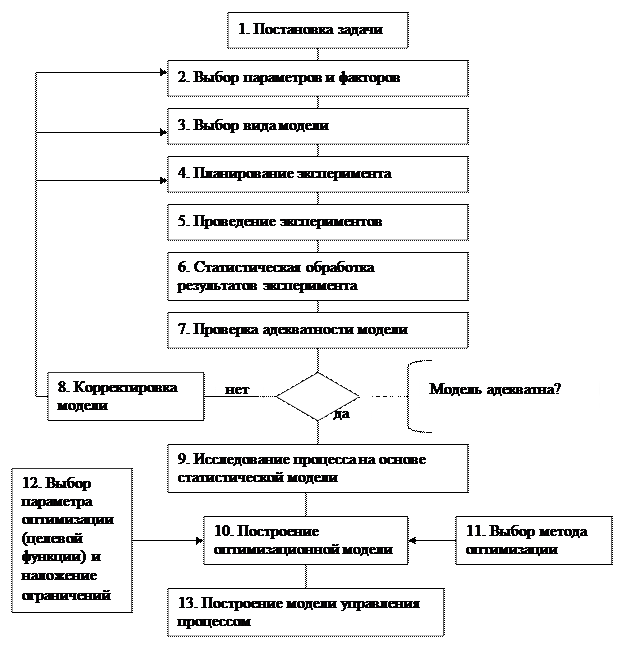
3. Построение матрицы планирования ДФЭ N=2^4-1

с использованием генерирующего соотношения

Генерируемое соотношение: х₁=х₃·х₄

При построении матрицы необходимо соблюдение следующих условий:

1. Условие симметрии: В матрице планирования сумма элементов каждого столбца должна быть рана нулю.

2. Условие нормирования: Равномерное расположение опытов на сфере относительно центра экспериментов.

3. Условие ортогональности: Сумма парных произведении двух любых столбцов должна быть равна нулю.

Для облегчения расчетов вводят столбец факторов х₀.

Таблица 1

Матрица планирования ДФЭ 2^4-1 (х₃=х₁·х₂) и результаты

Номер				Факторы				Результаты опытов
опыта	x0	x1	x2	x3	x4	x12	x24	x23	y
	+	+	+	+	+	+	+	+	18,8
	+	+	-	+	+	-	-	-	20,2
	+	-	+	+	-	-	-	+	15,6
	+	-	-	+	-	+	+	-	17,8
	+	-	+	-	+	-	+	-	18,1
	+	-	-	-	+	+	-	+	23,3
	+	+	+	-	-	+	-	-	20,2
	+	+	-	-	-	-	+	+	22,1
									20,2
									20,8
									19,3
b	19,51	0,8125	-1,3375	-1,4125	0,5875	0,5125	-0,3125	0,4375

статистической обработки данных экспериментов

Для повышения адекватности будущей модели вводят парные взаимодействия. С целью определения целесообразности этого шага необходимо произвести оценку эффекта смешивания линейных членов и парных взаимодействий. Для этого записываем генерирующее соотношение х₃=х₁·х₂ и путем его умножения на х₃ получаем формулу определяющего контраста 1=х₁·х₂·х₃. Далее, помножая обе стороны определяющего контраста на исследуемый фактор х_i, устанавливается система смешивания факторов. Получаем результат в следующем виде b_i→β_i+β_jk, т.е. выборочное значение коэффициента регрессии b_i получено путем смешивания образующих генеральную совокупность коэффициентов регрессии β_i и β_ik. Таким образом, фактор х_i смешан с парным взаимодействием факторов x_j и x_k.

Эффекты смешивания для линейных членов принимают следующий вид:

х₁: х₁=х₃·х₄; b₁→β₁+β₃₄;

х₂: х₂=х₁·х₂·х₃·х₄; b₂→β₂+β₁₂₃₄;

х₃: х₃=х₁·х₄; b₃→β₃+β₁₄;

х₄: х₄=х₁·х₃; b₄→β₄+β₁₃.

Эффекты смешивания парных взаимодействий имеют вид:

х₁х₂: х₁х₂= х₁·х₃·х₄; b₁₂→β₁₂+β₁₃₄;

х₁х₃: х₁х₃=х₄; b₁₃→β₁₃+β₄;

х₁х₄: х₁х₄=х₃; b₁₄→β₁₄+β₃;

х₂х₃: х₂х₃= х₁·х₂ ·х₄; b₂₃→β₂₃+β₁₂₄;

х₂х₄: х₂х₄= х₁·х₂·х₃; b₂₄→β₂₄+β₁₂₃;

х₃х₄: х₃х₄ =х₁; b₃₄→β₃₄+β₁.

Отсюда, для повышения адекватности модели включаем в нее дополнительные факторы: х₁х₂, х₂х₄, х₂х₃, т.к. взаимодействиями высоких порядков (третьего, четвертого и т.д.) принято пренебрегать из-за того, что они являются слабыми и не оказывают существенного влияния на характер парного взаимодействия.

4. Определение коэффициентов регрессии

Для построения неполной квадратичной модели:

,

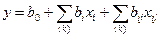необходимо рассчитать значения коэффициенты регрессии b₀, b_i, b_ij по формулам:

;

.

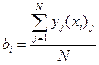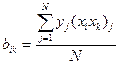Пример расчета коэффициента регрессии:

.

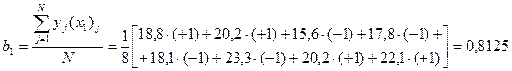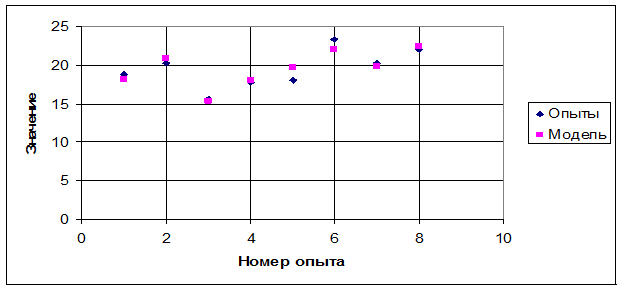
Рис. 1 Распределение опытных точек и точек полученных с помощью уравнения регрессии

5. Оценка значимости коэффициентов регрессии

Коэффициенты регрессии определены по результатам опытов, поэтому содержат в своей величине ошибку, связанную с их погрешностью. Если эта ошибка велика, то соответствующий коэффициент регрессии является незначимым и исключается из уравнения модели.

Статистическая значимость коэффициентов регрессии b_i оценивается с помощью t-критерия Стьюдента из сопоставления абсолютной величины b_i с ошибкой ее определения S_bi и вероятным отклонением ±∆b_i от расчетного значения b_i в пределах доверительного интервала.

Коэффициент регрессии является значимым, если выполняется следующее условие:

|b_i| ≥ ∆b_i = t(α, f)S_b.

Определение среднеквадратичного отклонения результатов опыта в нулевой точке (х_i=0) от их среднего:

,

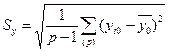где y_i0 – результаты повторных опытов в нулевой точке; 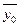– среднее значение из всех p повторных опытов в нулевой точке.

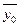= 20,1;

.

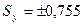Среднеквадратичная погрешность коэффициентов регрессии:

,

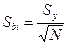где N – количество опытов по матрице.

.

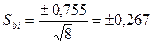Величина доверительного интервала:

∆b_i = t(α, f)S_b,

где t(α, f) – табличное значение t-критерия Стьюдента при заданном уровне значимости α и числе степеней свободы f=p-1.

При α=0,03: ∆b_i = 2,0 0,267 = 0,534 и значимым коэффициентом регрессии являются b₀, b₁, b₂, b₃, b₄. Тогда статистическая модель неполного квадратичного вида принимает следующую форму:

y = 19,51+0,8125x₁-1,3375x₂-1,4125x₃+0,5875x₄. (5.1)

6. Оценка адекватности модели

Проверка адекватности проводится путем сопоставления результатов моделирования по полученному уравнению регрессии (5.1) с результатами экспериментов по матрице планирования.

Вычисляем результаты моделирования по уравнению (5.1):

Пример вычисления:

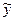₁ = 19,51+0,8125·(+1) -1,3375·(+1) -1,4125·(+1) +0,5875·(+1) = 18,16

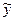₁ = 18,16;

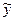₂ = 20,835;

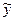₃ = 15,36;

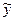₄ = 18,035;

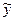₅ = 19,66;

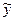₆ = 22,035;

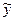₇ = 19,81;

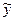₈ = 22,485.

Определяем дисперсию адекватности уравнения регрессии:

,

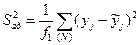где y_j и 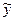_j – экспериментальные и расчетные значения параметра y при числе степеней свободы f₁ = N – (k+1), где N – количество опытов, k – число значимых коэффициентов регрессии.

.

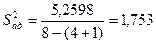Определяем значение F-критерия Фишера:

.

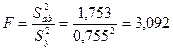Модель является адекватной, если выполняется следующее условие:
F ≤ F_табл(α, f₁, f₂),

где F_табл(α, f₁, f₂) – табличное значение F-критерия при уровне значимости α и числе степеней свободы f₁ – числителя (для дисперсной адекватности S²_ад) и f₂ – знаменателя (для среднеквадратичной ошибки опытов S_y).

3,092 ≤ F_табл(0,05, 4, 2) = 19,2

из чего следует, что разработанная модель адекватна.

7. Выводы

Разработанная неполная квадратичная модель имеет следующий вид:

y = 19,51+0,8125x₁-1,3375x₂-1,4125x₃+0,5875x₄.

Модель является адекватной, что позволяет использовать ее для изучения, оптимизации и управления процессом. Ортогональное планирование обеспечило отсутствие взаимной корреляции между факторами, благодаря чему, каждый коэффициент регрессии вычисляется независимым путем и в силу этого может быть подвержен физико-химической интерпретации.

Для увеличения точности модели можно изменить методику проведения экспериментов, проделать все опыты заново, но это дорого и сложно, поэтому для уменьшения погрешности можно произвести повторные опыты по матрице (иногда только в половине точек) и в качестве результатов экспериментов использовать их средние значения.