Числовые характеристики многомерных случайных величин

Рассмотрим основные числовые характеристики двумерной случайной величины (X, Y).

Начальный момент порядка k + s равен математическому ожиданию произведения Xk и Ys:

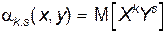. (2.1)

Центральный момент порядка k + s равен математическому ожиданию произведения центрированных величин 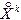и :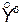

,

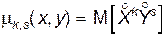где ;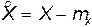

.

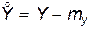Расчетные формулы:

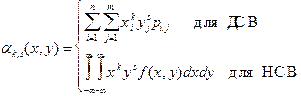, (2.3)

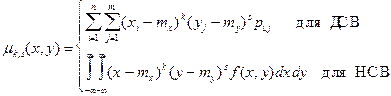, (2.4)

где pij - элементы матрицы вероятностей дискретной величины (X, Y);

f (x, y)-совместная плотность вероятности непрерывной величины (X, Y).

Рассмотрим наиболее часто используемые начальные и центральные моменты:

0,0(x, y) = 0,0(x, y) = 1; 1,0(x, y) = mx; 0,1(x, y) = my;

1,0(x, y) = 0,1(x, y)=0; 2,0(x, y) = 2(x); 0,2(x, y) = 2(y);

2,0(x, y) = Dx; 0,2(x, y) = Dy; 1,1(x, y) = Kxy.

Корреляционный момент Kxy характеризует степень линейной зависи­мости величин X и Y и рассеивание относительно точки (mx, my).

Вычислить Kxy можно и через начальные моменты:

Kxy = 1,1(x, y) - mxmy. (2.5)

Коэффициент корреляции rxy характеризует степень линейной зависи­мости величин

r xy= 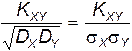. (2.6)

Для любых случайных величин | rxy | 1.

Если величины X и Y независимы, то rxy = 0.

Пример 2.1 Определить коэффициент корреляции величин X и Y (пример 1.1).

Решение. Определим математические ожидания величин X и Y по формуле (2.3):

mx = 1,0(x, y)= 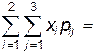00,1 + 00,2 + 00 + 10,2 + 10,3 + 10,2 = 0,7,

m y= 0,1(x, y)= 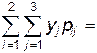-10,1 - 10,2 + 00,2 + 00,3 + 10 + 10,2 = -0,1.

Найдем значение Kxy по формуле (2.5)

Kxy = 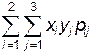- mxmy = 0(-1)0,1 + 000,2 + 010 +

1(-1)0,2 + 100,3 + 110,2 - 0,7(-0,1) = 0,07.

Определим дисперсии величин X и Y по формуле (2.4):

Dx = 2,0(x, y)= 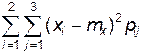= (-0,7)20,1 + (-0,7)20,2 +

+ (-0,7)20 + (0,3)20,2 + (0,3)20,3 + (0,3)20,2 = 0,21,

Dy = 0,2(x, y)= 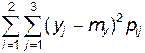= (-1,1)20,1 + (-1,1)20,2 +

+ (0,1)20,2 + (0,1)20,3 + (0,9)20 + (0,9)20,2 = 0,49. Значение коэффициента корреляции rxy вычислим по формуле

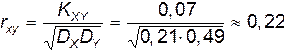. (2.6)

Пример 2.2 Двумерная случайная величина равномерно распределена в области D, ограниченной прямыми X = 0, Y = 0 и X + Y = 4. Определить коэффициент корреляции величин X и Y.

Решение. Запишем в аналитической форме совместную плотность вероятности:

.

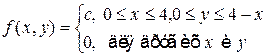Определим c, используя условие нормировки (1.5):

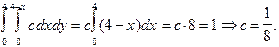
Найдем математическое ожидание и дисперсию величины X по формулам (2.3) и (2.4) соответственно:

m x= 1,0(x,y) = ;

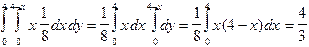D x= 2,0(x,y)= .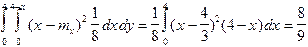

Так как область D симметрична относительно осей координат, то величины X и Y будут иметь одинаковые числовые характеристики: mx = my = 4/3, Dx = Dy = 8/9.

Определим корреляционный момент K xyпо формуле (2.5):

.

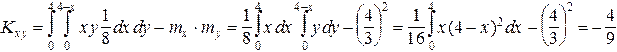Коэффициент корреляции величин X и Y будет равен (2.6):

.

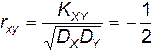ЗАДАЧИ

2.1. В продукции завода брак вследствие дефекта А составляет 3%, а вследствие дефекта B - 4.5%. Годная продукция составляет 95%. Найти коэффициент корреляции дефектов A и B.

Ответ: rab = 0.669.

2.2. Число X выбирается случайным образом из множества (1,2,3). Затем из того же множества выбирается наудачу число Y, равное или большее X. Найти коэффициент корреляции X и Y.

Ответ: rxy = 0,594.

2.3. Плотность вероятности двумерной случайной величины (X, Y) равна

.

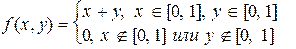Найти коэффициент корреляции X и Y.

Ответ: rxy = 0,091.

2.4. Плотность вероятности двумерной случайной величины (X, Y) равна

.

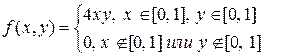Найти коэффициент корреляции X и Y.

Ответ: rxy = 0.