1.1. Непрерывность функции в точке
Определение. Функция у = f (x), определённая на интервале ] a, b [, называется непрерывной в точке х 0 Î ] a, b [, если 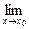 f (х) = f (х 0) (то есть предел функции равен её значению при предельном значении аргумента).
Так как равенство в определении равносильно следующему f (х) = f (х 0) (то есть предел функции равен её значению при предельном значении аргумента).
Так как равенство в определении равносильно следующему 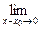 (f (х) – f (х 0)) = 0, то функция непрерывна в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции.
Теорема 1.1.1. Если функции f(x) и j(х) непрерывны в точке х (f (х) – f (х 0)) = 0, то функция непрерывна в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции.
Теорема 1.1.1. Если функции f(x) и j(х) непрерывны в точке х 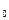 , то также непрерывны в этой точке их сумма f(x) + j(х), разность f(x) – j(х), произведение f(x)×j(х), а также частное , то также непрерывны в этой точке их сумма f(x) + j(х), разность f(x) – j(х), произведение f(x)×j(х), а также частное 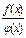 при условии, что j(х) ¹ 0.
Следствие 1. Целая рациональная функция Рn(х) = a 0 + a 1 x + a 2 x 2 + … + a n x n непрерывна при всех х.
Следствие 2. Дробно рациональная функция при условии, что j(х) ¹ 0.
Следствие 1. Целая рациональная функция Рn(х) = a 0 + a 1 x + a 2 x 2 + … + a n x n непрерывна при всех х.
Следствие 2. Дробно рациональная функция
 R(x) = R(x) = 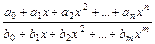 непрерывна при всех х, для которых знаменатель не обращается в нуль.
Теорема 1.1.2. Если функция j(х) непрерывна в точке х0, а функция f(у) непрерывна в точке у0 = j(х0), то сложная функция F(x) = f(j(х)) непрерывна в точке х0.
1.2 Точки разрыва функции
Рассмотрим функцию у = f (x), определённую на интервале ] a, b [, кроме, быть может, точки х 0 Î ] a, b [.
Определение. Точка х 0 называется точкой разрыва данной функции, если в ней функция определена, но не является непрерывной, или не определена в этой точке.
Если х 0 – точка разрыва функции f (x) и существуют конечные пределы
f (х 0 – 0) =
непрерывна при всех х, для которых знаменатель не обращается в нуль.
Теорема 1.1.2. Если функция j(х) непрерывна в точке х0, а функция f(у) непрерывна в точке у0 = j(х0), то сложная функция F(x) = f(j(х)) непрерывна в точке х0.
1.2 Точки разрыва функции
Рассмотрим функцию у = f (x), определённую на интервале ] a, b [, кроме, быть может, точки х 0 Î ] a, b [.
Определение. Точка х 0 называется точкой разрыва данной функции, если в ней функция определена, но не является непрерывной, или не определена в этой точке.
Если х 0 – точка разрыва функции f (x) и существуют конечные пределы
f (х 0 – 0) = 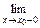 f (х), f (х 0 + 0) = f (х), f (х 0 + 0) = 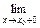 f (х), то она называется точкой разрыва первого рода.
Величина f (х 0 + 0) – f (х 0 – 0) называется скачком функции f (x) в точке х 0.
Пусть функция у = f (x) имеет разрыв в точке х 0 и f (х 0 + 0) = f (х 0 – 0), тогда х 0 называется точкой устранимого разрыва. Это название оправдано тем, что если доопределить такую функцию (если она не была определена в точке х 0), положив
f (х 0) = f (х), то она называется точкой разрыва первого рода.
Величина f (х 0 + 0) – f (х 0 – 0) называется скачком функции f (x) в точке х 0.
Пусть функция у = f (x) имеет разрыв в точке х 0 и f (х 0 + 0) = f (х 0 – 0), тогда х 0 называется точкой устранимого разрыва. Это название оправдано тем, что если доопределить такую функцию (если она не была определена в точке х 0), положив
f (х 0) = 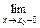 f (х) = f (х) = 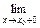 f (х), то получится функция, непрерывная в точке х 0.
Например, для функции f (x) = f (х), то получится функция, непрерывная в точке х 0.
Например, для функции f (x) = 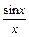 точка х 0 = 0 является точкой устранимого разрыва.
Если х 0 – точка разрыва и, по крайней мере, один из пределов f (х 0 + 0), f (х 0 – 0) является бесконечным или не существует, то х 0 называется точкой разрыва второго рода.
Например, 1) точка х 0 = 0 – точка разрыва второго рода для функции f (x) = точка х 0 = 0 является точкой устранимого разрыва.
Если х 0 – точка разрыва и, по крайней мере, один из пределов f (х 0 + 0), f (х 0 – 0) является бесконечным или не существует, то х 0 называется точкой разрыва второго рода.
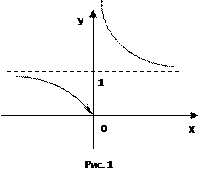
Например, 1) точка х 0 = 0 – точка разрыва второго рода для функции f (x) = 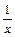 , поскольку f (х 0 – 0) = –¥, f (х 0 + 0) = +¥; 2) так как f (х 0 + 0) = +¥, то точка х 0 = 0 является точкой разрыва второго рода для функции f (x) = 3 , поскольку f (х 0 – 0) = –¥, f (х 0 + 0) = +¥; 2) так как f (х 0 + 0) = +¥, то точка х 0 = 0 является точкой разрыва второго рода для функции f (x) = 3  (см. рис. 1).
1.3. Непрерывность функции на промежутке
Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала. (см. рис. 1).
1.3. Непрерывность функции на промежутке
Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
  Если функция определена при х = а и при этом Если функция определена при х = а и при этом 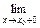 f (х) = f (а),
то говорят, что f (х) в точке а непрерывна справа. Аналогично, если f (х) = f (а),
то говорят, что f (х) в точке а непрерывна справа. Аналогично, если 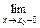 f (х) = f (b), то говорят, что в точке b эта функция непрерывна слева.
Определение. Функция называется непрерывной на отрезке [ a, b ], если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева).
Наибольшим значением функции у = f (x) на отрезке [ a, b ] называется такое её значение f (x 1), что f (x) £ f (x 1) для всех х Î [ a, b ].
Наименьшим значением функции у = f (x) на отрезке [ a, b ] называется такое её значение f (x 2), что f (x) ³ f (x 2) для всех х Î [ a, b ].
Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами.
Теорема 1.3.1. Функция, непрерывная на отрезке [a, b], достигает на нём своего наименьшего значения m и наибольшего значения M, то есть существуют такие точки x1 и x2 этого отрезка, что f(x1) = m, f(x2) = M.
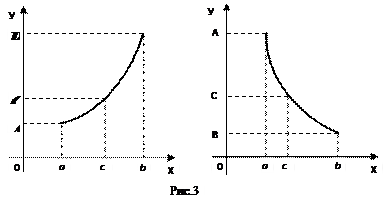
Теорема имеет простой геометрический смысл (см. рис.2).
Теорема 1.3.2. Если функция у = f(x) непрерывна на отрезке [a, b] и на его концах принимает неравные значения f(а) = А, f(b) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [a, b] такая, что f(с) = С.
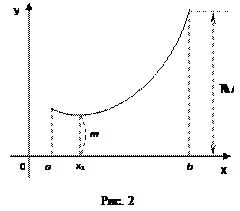
Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A < C < B (или A > C > B), пересекает график функции у = f (x).
Следствие. Если функция непрерывна на отрезке и на его концах принимает f (х) = f (b), то говорят, что в точке b эта функция непрерывна слева.
Определение. Функция называется непрерывной на отрезке [ a, b ], если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева).
Наибольшим значением функции у = f (x) на отрезке [ a, b ] называется такое её значение f (x 1), что f (x) £ f (x 1) для всех х Î [ a, b ].
Наименьшим значением функции у = f (x) на отрезке [ a, b ] называется такое её значение f (x 2), что f (x) ³ f (x 2) для всех х Î [ a, b ].
Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами.
Теорема 1.3.1. Функция, непрерывная на отрезке [a, b], достигает на нём своего наименьшего значения m и наибольшего значения M, то есть существуют такие точки x1 и x2 этого отрезка, что f(x1) = m, f(x2) = M.
Теорема имеет простой геометрический смысл (см. рис.2).
Теорема 1.3.2. Если функция у = f(x) непрерывна на отрезке [a, b] и на его концах принимает неравные значения f(а) = А, f(b) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [a, b] такая, что f(с) = С.
Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A < C < B (или A > C > B), пересекает график функции у = f (x).
Следствие. Если функция непрерывна на отрезке и на его концах принимает 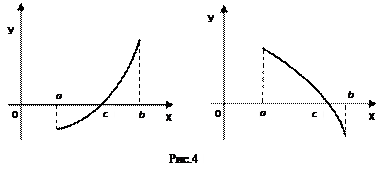 значения разных знаков, то на этом отрезке найдётся хотя бы одна точка, в которой функция обращается в нуль.
Геометрический смысл следствия иллюстрируется на рис.4.
Производная функции. Физический и геометрический смысл производной. Правила дифференцирования
Производная функции одно из основополагающих понятий математического анализа. Мы рассмотрим основные понятия и теоремы связанные с производной функции, также обсудим геометрический и физический смысл производной функции, приведем перечень правил, которые нужно соблюдать при вычислении производной функции одной переменной и сложной функции. значения разных знаков, то на этом отрезке найдётся хотя бы одна точка, в которой функция обращается в нуль.
Геометрический смысл следствия иллюстрируется на рис.4.
Производная функции. Физический и геометрический смысл производной. Правила дифференцирования
Производная функции одно из основополагающих понятий математического анализа. Мы рассмотрим основные понятия и теоремы связанные с производной функции, также обсудим геометрический и физический смысл производной функции, приведем перечень правил, которые нужно соблюдать при вычислении производной функции одной переменной и сложной функции.
|
1. Определение производной функции.
Необходимое условие существования производной
|
|
|
|
|
|
Пусть функция 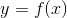 определена в точке
определена в точке 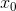 и некоторой ее окрестности. Придадим аргументу
и некоторой ее окрестности. Придадим аргументу 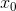 приращение
приращение 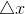 такое, что точка
такое, что точка 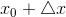 попадает в область определения функции. Функция при этом получит приращение
попадает в область определения функции. Функция при этом получит приращение 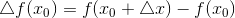 .
.
ОПРЕДЕЛЕНИЕ 1. Производной функции 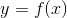 в точке
в точке 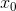 называется предел отношения приращения функции в этой точке к приращению аргумента
называется предел отношения приращения функции в этой точке к приращению аргумента 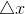 , при
, при  (если этот предел существует и конечен), т.е.
(если этот предел существует и конечен), т.е.
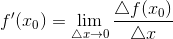 .
.
Следующая теорема устанавливает связь между существованием производной функции в точке 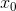 и непрерывностью функции в этой точке.
и непрерывностью функции в этой точке.
Теорема1. (необходимое условие существования производной функции в точке). Если функция y = f(x) имеет производную в точке 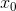 , то функция f(x) в этой точке непрерывна.
, то функция f(x) в этой точке непрерывна.
ДОКАЗАТЕЛЬСТВО
Пусть существует 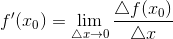 . Тогда
. Тогда
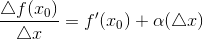 ,
,
Где 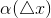 – бесконечно малая при
– бесконечно малая при  .
.
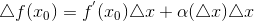 ;
;
.
Но это означает, что функция f(x) непрерывна в точке 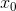 (по геометрическому определению непрерывности). ∎
(по геометрическому определению непрерывности). ∎
Замечание. Непрерывность функции в точке 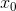 не является достаточным условием существования производной этой функции в точке
не является достаточным условием существования производной этой функции в точке 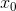 . Например, функция y = |x| непрерывна, но не имеет производной в точке
. Например, функция y = |x| непрерывна, но не имеет производной в точке 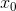 .
.
Очевидно, что соответствие 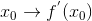 является функцией, определенной на некотором множестве
является функцией, определенной на некотором множестве 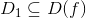 . Ее называют производной функции y = f(x) и обозначают
. Ее называют производной функции y = f(x) и обозначают
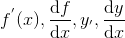 .
.
Операцию нахождения производной функции f(x) называют дифференцированием функции y = f(x).
2. Физический и геометрический смысл производной
 2015-10-13
2015-10-13 1242
1242








