Относительное, переносное и абсолютное движения точки. Абсолютная и относительная производные от вектора

В кинематике точки рассматривается движение точки относительно неподвижной системы координат. Но в некоторых случаях удобно изучать движение точки относительно двух систем отсчета, одна из которых определённым образом движется относительно второй, условно неподвижной системы координат.Например, автомобиль, который двигается поверхностью Земли, вместе с земным шаром вращается вокруг ее оси, а также перемещается в космическом пространстве, принимая участие в нескольких движениях.

Движение, при котором точка принимает участие в двух и больше движениях, называется сложным движением.

Рассмотрим сложное движение точки М, когда эта точка перемещается по подвижному телу А (рис. 106). Через произвольную точку О тела А проведем жестко связанные с ним оси Oxyz подвижной системы отсчета. Неподвижную систему отсчета 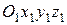свяжем с условно неподвижным телом, например с Землей.

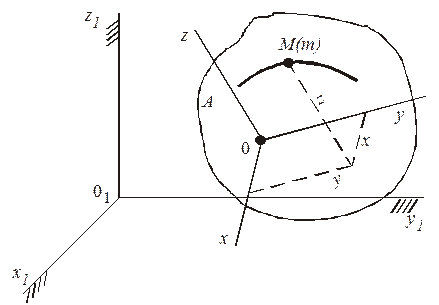
Рисунок 106

Движение точки М относительно неподвижной системы координат (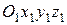) называют абсолютным. Траектория, скорость 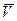и ускорение 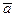точки М в абсолютном движении называют абсолютной траекторией, абсолютной скоростью и абсолютным ускорением.

Движение точки М относительно подвижной системы отсчета Oxyz называют относительным движением, а траектория, скорость 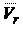и ускорение 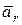точки в этом движении называют относительными.

Переносным называют движение подвижной системы координат Oxyz и неизменно связанного с ней тела относительно неподвижной системы отсчета 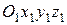. Переносной скоростью 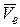и переносным ускорением 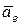будут скорость и ускорение той точки m тела (подвижной системы координат), с которой в данный момент времени совпадает подвижная точка М.

Основной задачей кинематики сложного движения точки является установление зависимостей между кинематическими характеристиками абсолютного, переносного и относительного движений.

При решении этой задачи необходимо дифференцировать переменный вектор в подвижной и неподвижной системах координат, определяя его производную по времени в отношении к подвижной системе (относительную или локальную производную), а также в отношении к неподвижной системе координат (абсолютную производную).

Установим связь между абсолютной и относительной производными от вектора 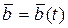, который изменяется в подвижной Oxyz и неподвижной 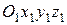системах отсчета (рис. 107).

В подвижной системе координат этот вектор определяется зависимостью

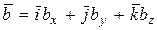(143)

где 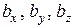– проекции вектора 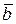на соответствующие оси подвижной системы.

Дифференцируя это векторное уравнение с учетом изменяемости орта 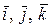в результате движения подвижной системы отсчета, одержимо:

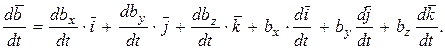(144)

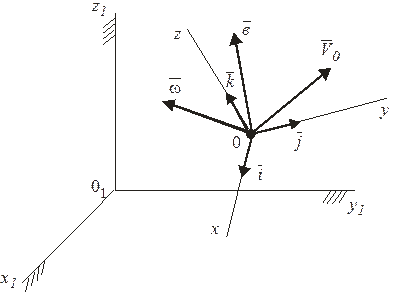
Рисунок 107

Первые три составляющих этого уравнения характеризуют изменение вектора 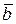в подвижной системе координат (при неизменном орте 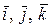) и являют собой относительную производную:

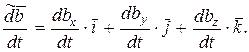(145)

Заменяя в раньше полученной формуле (122) скорости точки при вращательном движении тела

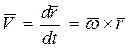
радиус-вектор 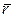последовательно на орт 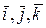, установим, что

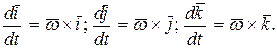
Следовательно, сумма трех последних составляющих уравнения (144) запишется так:

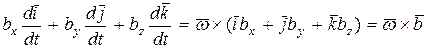. (146)

Подставляя (145) и (146) в (144), получим:

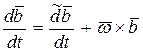. (147)

Следовательно, абсолютная производная вектора равняется сумме относительной производной этого вектора и векторного произведения угловой скорости подвижной системы координат на этот вектор.