И выборочные характеристики

При анализе какого-либо экономического показателя Х в фиксированный момент времени (либо без учета фактора времени) наблюдаемые его выборочные значения х ₁, х ₂, …, х_n обычно упорядочивают по возрастанию. Разность между максимальным и минимальным значением СВ Х называется размахом выборки.

Пусть количество различных значений в выборке равно k (k £ n). Значения x_i, i = 1, 2, …, k называются вариантами выборки. При этом х ₁ < x ₂ < … < x_k. Если значение х_i встретилось в выборке n_i раз, то число n_i называется абсолютной частотой значения х_i, а величина – относительной частотой значения х_i. Тогда наблюдаемые выборочные значения можно представить в виде вариационного (статистического) ряда (табл. 1.1).

Таблица 1.1

X	x 1 x 2 … xk
ni	n 1 n 2 … nk
	…

При этом , .

По вариационному ряду можно построить эмпирическую функцию распределения для СВ Х.

Эмпирической (выборочной) функцией распределения F_n (x) будем называть относительную частоту (статистическую вероятность) появления события, заключающегося в том, что СВ Х примет значение, меньше указанного х, т. е.:

F_n (x) = ω(X < x). (1.29)

По определению F_n (x) обладает следующими основными свойствами:

1. 0 £ F_n (х) £ 1.

2. F_n (x) = 0 при Х £ х ₁; F_n (x) = 1 при X > x_k.

Эмпирическая функция распределения F_n (x) является оценкой функции F (x) = P (X < x), которую в этом случае следует называть теоретической функцией распределения.

Пример 1.2. Анализируется прибыль Х (%) предприятий отрасли. Обследованы n = 100 предприятий, данные по которым занесены в следующий вариационный ряд [11]:

Х
ni
	0,05	0,2	0,4	0,25	0,1

Необходимо определить эмпирическую функцию распределения F_n (x) и построить ее график.

Рис. 1.7.

При большом объеме выборки ее элементы могут быть сгруппированы в интервальный вариационный ряд. Для этого n наблюдаемых значений выборки х ₁, х ₂, …, х_n разбивают на k непересекающихся интервалов равной ширины h (h – шаг разбиения). Пусть n_i – количество наблюдаемых значений СВ Х, попадающих в i -й интервал; – относительная частота попадания СВ Х в i -й интервал. Тогда интервальный вариационный ряд имеет вид:

Таблица 1.2

[ xi - 1, x)	[ x 0, x 1)	[ x 1, x 2)	…	[ xk - 1, xk)
ni	n 1	n 2	…   …	nk

Интервальный вариационный ряд наглядно может быть представлен в виде гистограммы – графика, где по оси абсцисс откладываются интервалы, на каждом из которых строятся прямоугольники с высотой и площадью, пропорциональной относительной частоте попадания СВ Х в данный интервал. На i -м интервале строится прямоугольник высотой 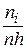. На основании гистограммы обычно выдвигают предположение о виде закона распределения исследуемой СВ Х.

Задача (гипотеза) о соответствии теоретического и статистического распределения обычно рассматривается с помощью статистического критерия Пирсона [16], основанного на распределении (Приложение 6).

Поскольку на практике обычно работают с выборкой, нас будут интересовать выборочные числовые характеристики, которые являются оценками соответствующих генеральных характеристик.

Если в формуле для математического ожидания дискретной СВ (1.4) положить равными вероятности каждого исхода p_i = 1/ n, то получим выборочное среднее арифметическое наблюдаемых значений выборки для СВ Х:

. (1.30)

При задании выборки в виде вариационного ряда

. (1.31)

Соответственно, для выборочной дисперсии получим формулы:

или (1.32)

.

Зачастую для вычисления D_в (Х) удобно использовать выражение:

. (1.33)

Выборочное среднее квадратическое отклонение определяется как

. (1.34)

При задании выборки в виде интервального вариационного ряда в формулах (1.31), (1.32) вместо x_i рассматривается среднее значение i -го интервала .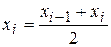

Выборочный коэффициент вариации V_в будет определяться процентным отношением выборочного среднего квадратического отклонения к выборочному среднему:

. (1.35)

Коэффициент вариации – безразмерная характеристика, удобная для сравнения величин рассеивания двух выборок, имеющих различные размерности.

Наиболее распространенными характеристиками взаимосвязи двух СВ являются меры их линейной связи – ковариация и коэффициент корреляции (см. раздел 1.4). Их оценками являются выборочная ковариация Cov_в (X, Y) и выборочный коэффициент корреляции r_xy.

, (1.36)

. (1.37)

Здесь .

Известно, что если величины X и Y независимы, то выборочный коэффициент корреляции равен нулю; если r_xy равен , то Y и X связаны линейной функциональной зависимостью [16].

Для нахождения выборочных ковариации и коэффициента корреляции необходимо иметь выборку объема n из двумерной генеральной совокупности (Х, Y), где рассматриваются пары значений x_i, y_i (i = 1, 2, …, n) в ряду наблюдений.

Выборочные оценки числовых характеристик генеральной совокупности обладают теми же основными свойствами, что и их теоретические прототипы.