Выпуклые функции и множества

7 8 9 10 11 12 13

Лабораторная работа № 4

Тема: Выпуклый анализ.

Рассматриваемые вопросы:

- выпуклые функции и множества

- основные свойства выпуклых и вогнутых функций:

- задача выпуклого программирования;

- выпуклая задача оптимизации;

- геометрическая интерпретация выпуклой задачи оптимизации;

- функция Лагранжа задачи выпуклого программирования;

- теоремаКуна – Таккера;

1. Постановка выпуклой задача оптимизации

Выпуклые функции и множества

Функция , заданная на выпуклом множестве Х, называется выпуклой, если для любых двух точек из Х и любого выполняется соотношение

. (1)

Функция , заданная на выпуклом множестве Х, называется вогнутой, если для любых двух точек из Х и любого выполняется соотношение

. (2)

Если неравенства (1) и (2) считать строгими и они выполняются при , то функция является строго выпуклой (строго вогнутой). Выпуклость и вогнутость функций определяется только относительно выпуклых множеств.

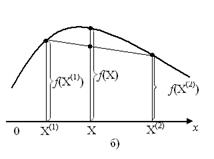
Рис. 1.

Если , – выпуклые (вогнутые) функции на некотором выпуклом множестве , то функция ‑ также выпуклая (вогнутая) на Х.

Основные свойства выпуклых и вогнутых функций:

1. Множество точек минимума выпуклой функции, заданной на выпуклом множестве, ‑ выпукло.

2. Пусть ‑ выпуклая функция, заданная на замкнутом выпуклом множестве . Тогда локальный минимум на Х является и глобальным.

3. Если глобальный минимум достигается в двух различных точках, то он достигается и в любой точке отрезка, соединяющего данные точки.

4. Если ‑ строго выпуклая функция, то ее глобальный минимум на выпуклом множестве Х достигается в единственной точке.

5. Пусть функция ‑ выпуклая функция, заданная на выпуклом множестве Х, и, кроме того, она непрерывна вместе со своими частными производными первого порядка во всех внутренних точках Х. Пусть – точка, в которой . Тогда в точке достигается локальный минимум, совпадающий с глобальным минимумом.

6. Множество точек глобальных (следовательно, и локальных) минимумов выпуклой функции , заданной на ограниченном замкнутом выпуклом множестве Х, включает хотя бы одну крайнюю точку; если множество локальных минимумов включает в себя хотя бы одну внутреннюю точку множества Х, то является функцией-константой.

Рассмотрим задачу нелинейного программирования

(3)

(4)

(5)

Для решения сформулированной задачи в такой общей постановке не существует универсальных методов. Однако для отдельных классов задач, в которых сделаны дополнительные ограничения относительно свойств функций , разработаны эффективные методы их решения.

Говорят, что множество допустимых решений задачи (3)–(5) удовлетворяет условию регулярности, или условию Слейтера, если существует по крайней мере одна точка , принадлежащая области допустимых решений такая, что .

2. Выпуклая задача оптимизации

Постановка задачи оптимизации: заданы множество Х и функция f (x), определенная на Х; требуется найти точки минимума или максимума функции f на X. Задачу на минимум будем записывать в виде

f(x) ® min, хÎ Х.

Задача называется выпуклой, если X – выпуклое множество, f – выпуклая функция на X.

Пример 1. Пусть дана задача

f(x) = x₂ ® min,

, , .

Ее геометрической интерпретацией служит рис.2. Отсюда видно, что решением задачи является «нижняя» точка пересечения окружности g₁(x) = 0 и прямой g₃(x) = 0, т.е. .

Пример 2 (задача поиска). Объект, подлежащий обнаружению, находится в одном из п районов с вероятностями р₁,..., р_п соответственно. Для поиска объекта имеется общий ресурс времени Т. Известно, что при поиске в i -м районе в течение времени t_i, вероятность обнаружения объекта (при условии, что он там находится) равна , где a_i > 0 – заданное число. Требуется так распределить время наблюдения по районам, чтобы максимизировать вероятность обнаружения объекта. Соответствующая задача оптимизации имеет вид

t_i ³ 0, i = 1, …, n.

Нетрудно проверить, что целевая функция задачи вогнута по t = (t₁, …, t_n). Переходя к минимизации этой функции, взятой с обратным знаком, получаем задачу выпуклого программирования.

3. Задача выпуклого программирования и функция Лагранжа

Задача (3)–(5) называется задачей выпуклого программирования, если функция является вогнутой (выпуклой), а функции – выпуклыми.

Функцией Лагранжа задачи выпуклого программирования (3)–(5) называется функция

где – множители Лагранжа.

Точка называется седловой точкой функции Лагранжа, если

для всех 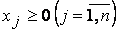и .

Теорема Куна – Таккера. Для задачи выпуклого программирования (3)–(5), множество допустимых решений которой обладает свойством регулярности, является оптимальным решением тогда и только тогда, когда существует такой вектор , что – седловая точка функции Лагранжа.

Если предположить, что функции и непрерывно дифференцируемы, то теорема Куна – Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка была седловой точкой функции Лагранжа, т. е. являлась решением задачи выпуклого программирования: