Постановка задачи. Случай дискретного времени

Математическая постановка задачи оптимального уп­равления любым динамическим объектом предполагает формиро­вание математической модели с определением области ее сущест­вования, выбор критерия оптимальности и, наконец, задание класса управлений с учетом той информации, которая может быть ис­пользована при реализации искомого оптимального управления.

В качестве математических моделей летательных аппаратов обычно выступают уравнения движения. Это - либо обыкновен­ные дифференциальные уравнения, либо их конечно-разностные аналоги. Первый случай соответствует непрерывному времени, второй - дискретному.

Изучение задач оптимизации целесообразно начать с рассмот­рения дискретного случая. Этому случаю в последнее время уде­ляется все большее внимание в связи с широким применением цифровой вычислительной техники не только при решении задач, связанных с исследованием вопросов динамики и управления ле­тательных аппаратов, но и непосредственно в процессе управления ими.

Итак, будем считать, что математическая модель летательного аппарата представляет собой систему конечно-разностных уравне­ний, которую в общем случае можно представить в виде

Здесь -мерный вектор фазовых координат, вектор состояния летательного аппарата; -мерный вектор управления; - мерный вектор случайных возмущений в i -й момент; -мерная вектор-функция; N — количество шагов (временных) управления. Ввиду того, что в правой части уравнения (4.1) присутствует случайный вектор, в общем случае вектор состояния также ока­зывается случайным.

Предполагается, что на вектор управления накладывается ог­раничение вида , где под понимается допустимое множе­ство векторов в i -й момент.

Считается, что статистические характеристики случайных век­торов , полностью известны. Не нарушая общности, можно считать, что вектор состояния в начальный момент х₀ известен точно. Возможные случайные разбросы начальных условий включаются в состав вектора .

Примером модели (4.1) может служить модель космического аппарата в задаче о многоимпульсной коррекции его траектории. В этом случае вектором состояния является совокупность эле­ментов орбиты перед i -й коррекцией. В качестве вектора управле­ния выступает корректирующий импульс скорости в i -й момент. Векторы возмущений включают в себя ошибки ре­ализации корректирующих импульсов, ошибки знания векторов состояния и т. д. Вектор-функция устанавливает связь между элементами орбиты до и после совершения коррекции. Чис­ло N характеризует количество коррекций. Условие отра­жает тот факт, что любой корректирующий импульс в общем слу­чае ограничен по величине и определяется запасом топлива на бор­ту аппарата.

Задача программирования оптимального управления заключа­ется в определении такой последовательности , обозначаемой для кратности через и, которая с учетом имеющихся огра­ничений обеспечивает перевод системы (4.1) из заданного началь­ного состояния х₀ в конечное состояние 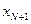с минимальным значе­нием некоторого критерия. При этом на вектор конечного состоя­ния 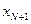в общем случае могут быть наложены дополнительные ограничения, характеризующие, например, допустимые конечные ошибки выведения летательного аппарата.

В качестве основного критерия оптимальности в дальнейшем принимается терминальный критерий, равный математическому ожиданию некоторой скалярной функции конечного состояния

Таким образом, минимизации подлежит величина

Здесь и далее символ (—) используется для более компактного обозначения математического ожидания. В соответствии с опреде­лением математического ожидания в развернутом виде выражение (4.2) имеет следующий вид:

где p(x_N+l) —плотность распределения вероятностей случайного вектора x_N+1; X_N+1 —допустимое множество всех случайных век­торов; dx_N+1 — элементарный объем этого множества. Интеграл в данном выражении следует понимать как многомерный.

Следует отметить, что выбор критерия оптимальности в виде (4.2) не нарушает общности рассмотрения задачи. Действительно, критерий более общей (интегротерминальной) структуры

легко сводится к виду (4.2):

правда, в отношении вектора, расширенного на одну дополнитель­ную компоненту , определяемую уравнением

с начальным условием .

Первое слагаемое в критерии (4.3) характеризует качество уп­равления (в интегральном смысле, второе — эффект управления конечным состоянием. Так, в задаче коррекции траектории космиче­ского аппарата слагаемое может оценивать расход топлива

при коррекции или энергетические затраты, а функция — определять конкретную характеристику конечной точности процес­са коррекции.

Итак, пусть сформирована математическая модель объекта уп­равления, определена область ее существования и выбран крите­рий оптимальности. Для завершенности постановки задачи опти­мального управления остается определить класс управлений, в ко­тором будет искаться оптимальное управление. При этом помимо ограничений, накладываемых на управление, важно уточнить ту информацию, которая может быть использована при реализации искомого управления. В рассматриваемом случае, т. е. при опреде­лении программы управления, дело обстоит просто — здесь ника­кой информации для реализации управления использовать не предполагается. При решении в последующем задачи синтеза это обстоятельство является принципиальным.