Тема 7. Оптимизационные задачи. Текстовые задачи с графическим решением
Оптимизационные задачи линейного программирования
Оптимизационной задачей называется задача нахождения экстремума (максимума или минимума) целевой функции при наличии некоторой системы линейных или нелинейных ограничений. Часто оптимизационные задачи задаются в виде текстовых задач, когда перед решением нужно сначала составить систему уравнений и неравенств. Такие задачи постоянно встречаются в ЕГЭ и на ДВИ.
Начнем рассмотрение темы со случаев, когда и целевая функция, и система ограничений заданы линейно.
В общем виде задача выглядит так:
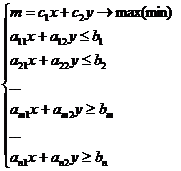
Здесь числа а и с – произвольные числа. Задача может быть направлена как на максимум, так и на минимум. При этом ограничения могут быть как меньше или равны нулю, так и больше или равны нулю.
Пример 1. Оптимизационная задача с использованием понятия градиента
Найти наибольшее и наименьшее значение параметра а, при котором выполняется следующая система:
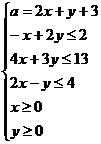
Важные термины:
Линии уровня - линии, которые может задавать уравнение целевой функции с учетом значений параметра.
Градиент (от лат. gradiens, род. падеж gradientis – шагающий, растущий) – вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой, а по величине (модулю) равный скорости роста этой величины в этом направлении.
Градиент является вектором нормали, перпендикулярным линиям уровня – линии уровня будут двигаться вдоль этого вектора. Как мы знаем из лекции 2, если уравнение прямой задано в общем виде 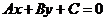 , то нормальный вектор задается как
, то нормальный вектор задается как 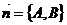 .
.
 2017-12-14
2017-12-14 287
287







