ІІІ. Функції багатьох змінних

Задача 1.

1. Величина z називається функцією двох змінних х і у, якщо кожній впорядкованій парі (х, у) значень двох незалежних одна від одної змінних х і у з деякої області D площини Оху відповідає єдине значення величини z.

Позначається функція двох змінних z = f (х, у), або z = F (х, у), або z = z (х, у).

2. Множина D всіх точок (х, у), при яких z = f (х, у) має сенс, називається областю визначення функції, а множина значень z, що приймає функція при (х, у) 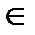D, називається множиною значень функції.

Задача 2.

1. Розглянемо функцію двох змінних z = f (х, у). Позначимо приріст функції по змінній х при фіксованому значенні у, як Δ_х z = f (х + Δ х, у) – f (х, у), де Δ х – приріст х. Аналогічно, Δ _уz = f (х, у + Δ у) – f (х, у), де Δ у – приріст у.

2. Частинною похідною по х від функції z = f (х, у) називається границя відношення приросту функції по х Δ _хz до приросту змінної х, якщо останній прямує до нуля:

3. Частинна похідна від функції z = f (х, у) по у визначається аналогічно:

4. Частинну похідну по х позначають: , , , , .Частинну похідну по у можна позначити , , , , .

5. При обчисленні похідної по змінній у постійною вважається х. Саме обчислення здійснюється за тими ж правилами і формулами, що і у функції однієї

змінної (див. частину 1 даних вказівок).

6. Щоб довести дану в задачі рівність треба обчислити частинні похідні від функції z = f (х, у). Потім підставити знайдені похідні в рівняння і виконати всі можливі тотожні перетворення. В результаті маємо отримати вірну рівність.

Задача 3.

1. Точка М ₀ (x ₀; y ₀) називається точкою екстремуму (максимуму чи мінімуму) функції z = f (х; у), якщо f (x ₀; y ₀) є відповідно найбільше чи найменше значення функції f (х; у) в деякому околі точки М ₀ (x ₀; y ₀): f (x ₀; y ₀) > f (х; у) чи f (x ₀; y ₀) << f (х; у) в усіх точках М (х; у) ≠ М ₀ (x ₀; y ₀) з деякого околу точки М ₀.

2. Значення f (x ₀; y ₀) називається максимальним (або мінімальним) значенням функції.

3. Необхідна умова екстремуму. Якщо в точці М ₀ (x ₀; y ₀) диференційована функція z = f (х; у) має екстремум, то її частинні похідні в цій точці дорівнюють нулю:

і .

Точка М ₀ (x ₀; y ₀), в якій обидві частинні похідні дорівнюють нулю, називається стаціонарною.

4. Якщо функція z = f (х, у) має частинні похідні і , то вони в загальному випадку також є функціями двох змінних. Частинні похідні від цих функцій називаються другими частинними похідними від функції z = f (х, у) і позначаються так:

, , , .

Похідні та називаються мішаними.

5. Достатня умова екстремуму. Нехай точка М ₀ (x ₀; y ₀) є стаціонарною точкою функції z = f (х; у). Позначимо

, , .

Якщо АС – В ²> 0 і А < 0, то М ₀ (x ₀; y ₀) – точка максимуму.

Якщо АС – В ²> 0 і А > 0, то М ₀ (x ₀; y ₀) – точка мінімуму.

Якщо АС – В ²< 0, то М ₀ (x ₀; y ₀) не є точкою екстремуму.

Якщо АС – В ² = 0, то необхідне додаткове дослідження.

6. Щоб знайти екстремум функції двох змінних z = f (х; у) треба:

– знайти область визначення функції;

– знайти частинні похідні і прирівняти їх до нуля;

– скласти з отриманих рівнянь систему і розв’язати її; знайдені точки є стаціонарними;

– обчислити частинні похідні другого порядку від функції z = f (х; у);

– знайти значення А, В, С в кожній із стаціонарних точок;

– знайти величину АС – В ²і зробити висновок;

– якщо в досліджуваній стаціонарній точці є екстремум, то підставити координати точки в функцію z = f (х; у). Знайдене значення буде максимальним (або мінімальним) значенням функції.

Задача 4.

1. Градієнтом функції z = f (х; у) називається вектор, координатами якого є частинні похідні цієї функції

2. Градієнт функції вказує напрямок, в якому функція зростає скоріше за всі інші напрямки.

3. Щоб знайти градієнт функції в точці М треба її координати підставити замість х та у відповідно у вираз для градієнта.

Задача 5.

1. Якщо задана функція z = f (х; у) і напрямок , то границя відношення приросту функції Δ f до Δ ρ при Δ ρ → 0 називається похідною функції за напрямком і позначається

де , Δ х, Δ у – приріст аргументів х та у відповідно вздовж напрямку .

2. Величина похідної за напрямком визначає швидкість зміни функції в цьому напрямку. Знак похідної – характер зміни. Якщо > 0, то функція зростає у напрямку , якщо < 0, то функція спадає за цим напрямком.