Опираясь на формулу (3), выведем основные свойства неопределенного интеграла.
I. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции.
Это свойство непосредственно вытекает из определения неопределенного интеграла.
Таким образом, имеем
 и
и 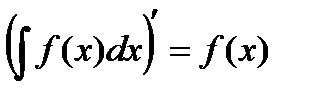 . (4)
. (4)
II. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого.
В самом деле, пусть 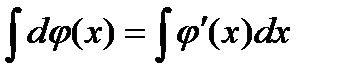 , где функция
, где функция 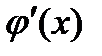 непрерывна. Функция
непрерывна. Функция 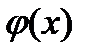 , очевидно, является первообразной для
, очевидно, является первообразной для 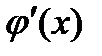 . Поэтому имеем
. Поэтому имеем
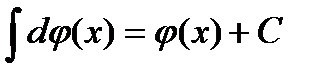 . (5)
. (5)
Замечание: В формулах (4) и (5) знаки d и 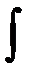 , следующие друг за другом в том или другом порядке, взаимно уничтожают друг друга (если не учитывать постоянного слагаемого). В этом смысле дифференцирование и интегрирование и являются взаимно обратными математическими операциями.
, следующие друг за другом в том или другом порядке, взаимно уничтожают друг друга (если не учитывать постоянного слагаемого). В этом смысле дифференцирование и интегрирование и являются взаимно обратными математическими операциями.
III. Отличный от нуля постоянный множитель можно выносить за знак неопределенного интеграла, т.е. если постоянная А ≠ 0, то
|
|
|
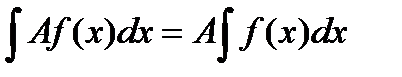 . (6)
. (6)
В самом деле, пусть F(x) - первообразная для f(x). В силу формулы (3) имеем: 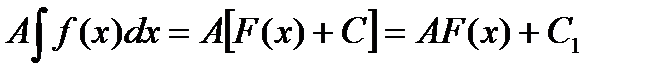 , (7)
, (7)
где С1=АС, причем С и С1 – произвольные постоянные при А ≠ 0. Но AF(x) есть первообразная для функции Af(x), так как
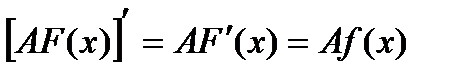 .
.
Поэтому из формулы (7) получаем требуемую формулу (6).
Замечание: При А=0 формула (3) неверна, так как левая часть ее представляет собой произвольную постоянную, а правая часть тождественна равна нулю.
IV. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме неопределенных интегралов от этих функций, т.е. если, например, функция f(x), g(x), h(x) непрерывны в интервале (a,b), то
 при х
при х 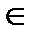 (a,b). (8)
(a,b). (8)
Действительно, пусть F(x),G(x),H(x) – первообразные соответственно функций f(x), g(x), h(x). На основании формулы (3) имеем:
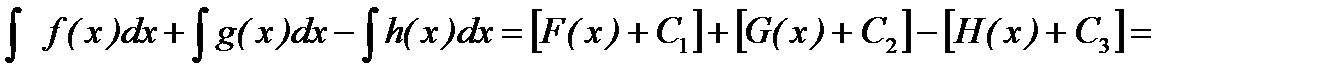

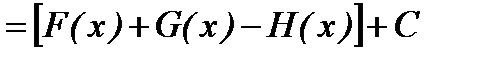 , (9)
, (9)
где С1, С2, С3 − произвольные постоянные и С=С1+С2-С3, очевидно, также является произвольной постоянной. Но функция F(x)+G(x)-H(x) есть первообразная для функции f(x)+g(x)-h(x), так как
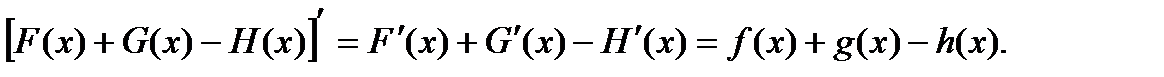
Следовательно,
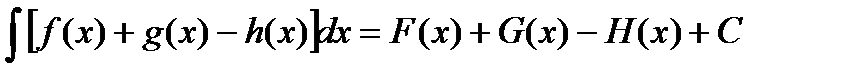 . (10)
. (10)
Из формул (9) и (10) вытекает равенство (8).
Зная формулы для производных основных элементарных функций, можно составить таблицу неопределенных интегралов (первообразных), которую мы дополним еще несколькими часто встречающимися интегралами.
Таблица основных интегралов (ТОИ)
1. 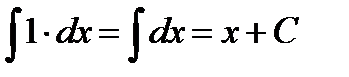
2. 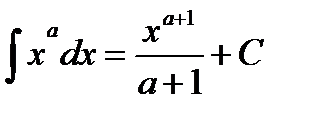 ,
, 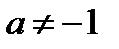
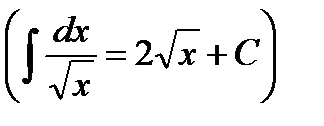
3. 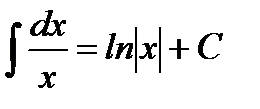
4. 
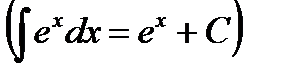
5. 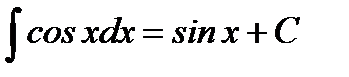 6.
6. 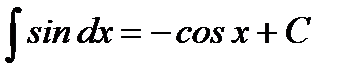
7. 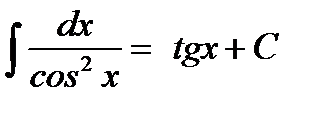 8.
8. 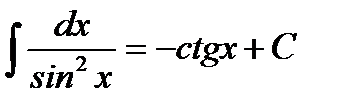
9. 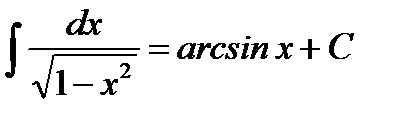 10.
10. 
11. 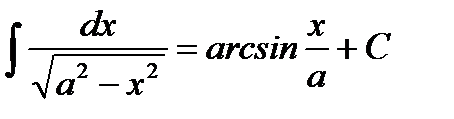 12.
12. 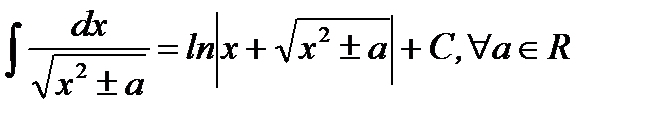
13. 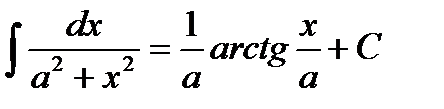 14.
14. 
 2017-12-14
2017-12-14 730
730








