Непрерывно-стохастические модели 1 страница

(Q -СХЕМЫ)

 

Особенности непрерывно-стохастического подхода рассмотрим на примере использования в качестве типовых математических схем систем массового обслуживания (англ. queueingsystem), которые будем называть Q-схемами. Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживании и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания [6, 13, 33, 37, 51].

Основные соотношения. В качестве процесса обслуживания могут быть представлены различные по своей физической природе процес­сы функционирования экономических, производственных, техничес­ких и других систем, например потоки поставок продукции некото­рому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удаленных терминалов и т. д. При этом характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т. е. стохастический характер процесса их функционирова­ния. Остановимся на основных понятиях массового обслуживания, необходимых для использования Q-схем, как при аналитическом, так и при имитационном.

В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и со­бственно обслуживание заявки. Это можно изобразить в виде неко­торого i -гo прибора обслуживания П_i (рис. 2.6), состоящего из накопителя заявок Н_i, в котором может одновременно находиться заявок, где — емкость i -гo накопителя, и канала об­служивания заявок (или просто канала) K_i. На каждый элемент прибора обслуживания П_i поступают потоки событий: в накопитель Н_i — поток заявок w_i, на канал K_i — поток обслуживаний u_i.

Потоком событий называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных собы­тий. Поток событий называется однородным, если он характеризу­ется только моментами поступления этих событий (вызываю­щими моментами) и задается последовательностью , где 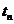— момент наступления n-го собы­тия — неотрицательное вещественное число. Однородный поток событий также может быть задан в виде последовательности про­межутков времени между 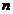-м и 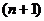-м событиями , которая однозначно связана с последовательно­стью вызывающих моментов , где , , , т.е. .

Потоком неоднородных событий на­зывается последовательность где — вызывающие моменты; — набор признаков события. Например, примени­тельно к процессу обслуживания для не­однородного потока заявок могут быть заданы принадлежность к тому или иному источнику заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т. п.

 

Рассмотрим поток, в котором события разделены интервалами времени , ,...,.., которые вообще являются случайными величинами. Пусть интервалы , ,... независимы между собой. Тогда поток событий называется потоком с ограниченным последействием.

Пример потока событий приведен на рис 2.7, где обозначено — интервал между событиями (случайная величина); — время наблюдения, — момент совершения события.

Интенсивность потока можно рассчитать экспериментально по формуле

где N — число событий, произошедших за время наблюдения . Если или определено какой-либо формулой , то поток называется детерминирован­ным. Иначе поток называется случайным.

Случайные потоки бывают:

— ординарными, когда вероятность одновременного появления 2-х и более
событий равна нулю;

— стационарными, когда частота появления событий постоянная;

— без последействия, когда вероятность не зависит от момента совершения
предыдущих событии.

Поток событий называется ординарным, если вероятность того, что на малый интервал времени ,примыкающий к моменту времени , попадает больше одного события , пренебрежительно мала по сравнению с вероятностью того, что на этот же интервал времени попадает ровно одно событие , т. е. . Если дли любого интервала событие

как сумма вероятностей событий, образующих полную группу и несовместных, то для ординарного потока событий

где — величина, порядок малости которой выше, чем ,т. е.

Стационарным потоком событий называется поток, для которого вероятность появления того или иного числа событий на интервале времени зависит лишь от длины этого участка и не зависит от того, где на оси времени взят этот участок.

Рассмотрим на оси времени ординарный поток событий и найдем среднее число событий, наступающих на интервале времени , примыкающем к моменту времени . Получим

Тогда среднее число событий, насту­пающих на участке времени , в единицу времени, составит . Рассмот­рим предел этого выражения при . Если этот предел существует, то она называется интенсивностью (плотностью) ординарного потока событий .Интенсивность потока может быть любой неотрицательной функцией времени, имеющей размерность, обратную размерности времени. Для стационар­ного потока его интенсивность не зависит от времени и представляет собой постоян­ное значение, равное среднему числу событий, наступающих в единицу времени .

Возможные приложения. Обычно в приложениях при моделиро­вании различных систем применительно к элементарному каналу обслуживания можно считать, что поток заявок , т. е. интервалы времени между моментами появления заявок (вызыва­ющие моменты) на входе ,образует подмножество неуправля­емых переменных, а поток обслуживания , т. е. интервалы времени между началом и окончанием обслуживания заявки, об­разует подмножество управляемых переменных.

Заявки, обслуженные каналом ,и заявки, покинувшие прибор по различным причинам необслуженными (например, из-за переполнения накопителя ), образуют выходной поток , т. е. интервалы времени между моментами выхода заявок образуют подмножество выходных переменных.

Процесс функционирования прибора обслуживания можно представить как процесс изменения состояний его элементов во времени . Переход в новое состояние для означает изменение количества заявок, которые в нем находятся (в канале и в накопи­теле ). Таким образом, вектор состояний для имеет вид , где — состояние накопителя ( — накопитель пуст, — в накопителе имеется одна заявка,..., — накопи­тель полностью заполнен); — емкость накопителя , измеря­емая числом заявок, которые в нем могут поместиться; — состо­яние канала ( — канал свободен, — канал занят и т.д.).

В практике моделирования систем, имеющих более сложные структурные связи и алгоритмы поведения, для формализации ис­пользуются не отдельные приборы обслуживания, а Q-схемы, об­разуемые композицией многих элементарных приборов обслужива­ния (сети массового обслуживания). Если каналы различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы и их параллельные композиции соединены последовате­льно, то имеет место многофазное обслуживание (многофазная Q-схема). Таким образом, для задания Q-схемы необходимо ис­пользовать оператор сопряжения R, отражающий взаимосвязь эле­ментов структуры (каналов и накопителей) между собой.

Связи между элементами Q-схемы изображают в виде стрелок (линий потока, отражающих направление движения заявок). Раз­личают разомкнутые и замкнутые Q-схемы. В разомкнутой Q-схеме выходной поток обслуженных заявок не может снова поступить на какой-либо элемент, т. е. обратная связь отсутствует, а в замкнутых Q-схемах имеются обратные связи, по которым заявки двигаются в направлении, обратном движению вход-выход.

Собственными (внутренними) параметрами Q-схемы будут яв­ляться количество фаз , количество каналов в каждой фазе , , количество накопителей каждой фазы , , ем­кость i -ro накопителя . Следует отметить, что в теории мас­сового обслуживания в зависимости от емкости накопителя приме­няют следующую терминологию для систем массового обслужива­ния: системы с потерями (, т. е. накопитель в приборе отсутствует, а имеется только канал обслуживания ), системы с ожиданием (, т. е. накопитель имеет бесконечную ем­кость и очередь заявок не ограничивается) и системы смешанного типа (с ограниченной емкостью накопителя ).Всю совокупность собственных параметров Q-схемы обозначим как подмножество .

Для задания Q-схемы также необходимо описать алгоритмы ее функционирования, которые определяют набор правил поведения заявок в системе в различных неоднозначных ситуациях. В зависи­мости от места возникновения таких ситуаций различают алгорит­мы (дисциплины) ожидания заявок в накопителе и обслуживания заявок каналом каждого элементарного обслуживающего прибо­ра Q-схемы. Неоднородность заявок, отражающая процесс в той или иной реальной системе, учитывается с помощью введения клас­сов приоритетов.

В зависимости от динамики приоритетов в Q-схемах различают статические и динамические приоритеты. Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы, т. е. они являются фиксированными в пределах решения конкретной задачи моделирования. Динамические приоритеты возникают при модели­ровании в зависимости от возникающих ситуаций. Исходя из пра­вил выбора заявок из накопителя на обслуживание каналом ,можно выделить относительные и абсолютные приоритеты. От­носительный приоритет означает, что заявка с более высоким при­оритетом, поступившая в накопитель , ожидает окончания об­служивания предшествующей заявки каналом и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель ,пре­рывает обслуживание каналом заявки с более низким приорите­том и сама занимает канал (при этом вытесненная из заявка может либо покинуть систему, либо может быть снова записана на какое-то место в ).

При рассмотрении алгоритмов функционирования приборов об­служивания (каналов и накопителей )необходимо также задать набор правил, по которым заявки покидают и : для — либо правила переполнения, по которым заявки в зависимо­сти от заполнения покидают систему, либо правила ухода, связанные с истечением времени ожидания заявки в , для — правила выбора маршрутов или направлений ухода. Кроме того, для заявок необходимо задать правила, по которым они остаются в канале или не допускаются до обслуживания каналом , т. е. правила блокировок канала. При этом различают блокировки по выходу и по входу. Такие блокировки отражают наличие управля­ющих связей в Q-схеме,регулирующих поток заявок в зависимости от состояний Q-схемы. Весь набор возможных алгоритмов поведе­ния заявок в Q-схеме можно представить в виде некоторого опера­тора алгоритмов поведения заявок А.

Таким образом, Q-схема, описывающая процесс функциониро­вания системы массового обслуживания любой сложности, одно­значно задается в виде Q=<W, U, H, Z, R, А>.

При ряде упрощающих предположений относительно подмно­жеств входящих потоков W и потоков обслуживания U (выполнение условий стационарности, ординарности и ограниченного последей­ствия) оператора сопряжения элементов структуры R (однофазное одноканальное обслуживание в разомкнутой системе), подмножест­ва собственных параметров Н (обслуживание с бесконечной ем­костью накопителя), оператора алгоритмов обслуживания заявок А (бесприоритетное обслуживание без прерываний и блокировок) для оценки вероятностно-временных характеристик можно исполь­зовать аналитический аппарат, разработанный в теории массового обслуживания. При принятых предположениях в обозначениях Д. Кендалла будет иметь место классическая система обслуживания типа М/М/1 (одноканальная система с марковским входящим пото­ком заявок и марковским потоком обслуживания). Рассмотрим на примере основные аналитические соотношения для такой элемен­тарной Q-схемы [6, 24, 37].

 

Пример 2.6. Допустим, что процесс обслуживания начинается при отсутствии заявок в накопителе. Тогда состояния системы массового обслуживания описыва­ются следующей системой уравнений:

где — вероятность нахождения системы в состоянии в момент време­ни t,т. е. когда в ней имеется n заявок.

Эти уравнения следуют из того, что вероятность нахождения в системе я заявок» момент времени равна вероятности нахождения в системе n заявок в момент t, умноженной на вероятность того, что за время в систему не поступит ни одной заявки и ни одна заявка не будет обслужена, плюс вероятность нахождения в системе заявок в момент t, умноженная на вероятность того, что за время поступит одна заявка, и ни одна заявка не будет обслужена, плюс вероятность нахождения в системе заявок в момент t,умноженная на вероятность того, что за время одна заявка покинет систему и не поступит ни одной заявки. Вероятность того, что за время не поступит ни одной заявки и ни одна заявка не покинет систему, равна . Член, содержащий , при составлении дифференциального уравнения опускается. Следовательно, можно записать . Относительно остальных двух членов первого уравнения заметим, что

Перевеся влево и устремив к нулю, получим систему дифференциальных уравнений

Найдем выражение для математического ожидания числа заявок, находящихся в накопителе, и среднего времени ожидания заявок в накопителе для стационарного состояния .Приравняв нулю производные по времени в исключив, таким образом, время t из уравнений, получим систему алгебраических уравнений

Пусть в первом уравнении . Тогда . Подставив сюда значение из второго уравнения, находим . Повторяя эти операции, получаем ,причем , так как это сумма вероятностей того, чтов системе нет ни одной заявки, имеется одна заявка, две заявки и т. д. Сумма этих вероятностей должна быть равна единице, так как рассматриваются все возможные

состояния системы. Поэтому , или , откуда . Следовательно, .Полученное выражение представляет собой геометрическое распределение.

Математическое ожидание числа заявок, находящихся в системе (проборе),

Отметим, что — среднее значение и возможны колебания числа заявок, ожида­ющих обслуживания, что можно оценить с помощью дисперсии:

При этом

Следовательно,

Математическое ожидание числа заявок, находящихся в накопителе,

Среднее время ожидания заявок в накопителе

 

Возможности оценки характеристик с использованием аналити­ческих моделей теории массового обслуживания являются весьма ограниченными по сравнению с требованиями практики исследова­ния и проектирования систем, формализуемых в виде Q-схем. Не­сравненно большими возможностями обладают имитационные мо­дели, позволяющие исследовать Q-схему, задаваемую Q=<W, U, H, Z, Y, R, А>,без ограничений. На работу с Q-схемами при машинной реализации моделей ориентированы многие языки имитационного моделирования, например SIMULA, SIMSCRIPT, GPSS и др. Дета­льно вопросы, связанные с имитационным моделированием Q-схем, будут рассмотрены далее.

 

2.6. СЕТЕВЫЕ МОДЕЛИ (N -СХЕМЫ)

 

В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом при­чинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Самым распростра­ненным в настоящее время формализмом, описывающим структуру и взаимодействие параллельных систем и процессов, являются сети Петри (англ. PetriNets), предложенные К. Петри [28, 30].

Основные соотношения. Теория сетей Петри развивается в нес­кольких направлениях: разработка математических основ, структур­ная теория сетей, различные приложения (параллельное програм­мирование, дискретные динамические системы и т. д.).