2018-01-08
1085Линейное программирование – один из первых и наиболее подробно изученных разделов математического программирования в смысле нахождения оптимальных значений переменных. Можно сказать, что линейное программирование применимо для решения математических моделей тех процессов и систем, в основу которых может быть положена гипотеза линейного описания реальных экономических процессов.
Нелинейное программирование – если хотя бы одна из функций (целевая или в ограничениях – нелинейная). Задача оптимизации функции полезности (потребительского предпочтения)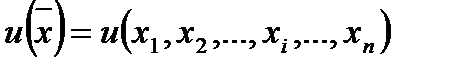 
при ограничениях на бюджет 
, 
, 
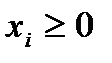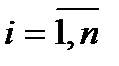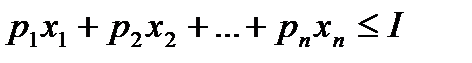- нелинейная. Здесь 
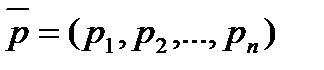— вектор цен на набор из n продуктов 
, 
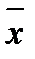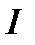— доход индивида, который он готов потратить на приобретение набора продуктов 
.
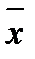Функция оценивает уровень удовлетворения потребителя при приобретении им данного набора товаров. Неоклассическая функция полезности: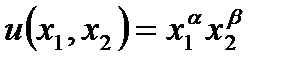 
, 
, 
;
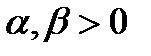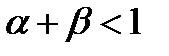Функция полезности (аналитическая) имеет 3 свойства:
1) 
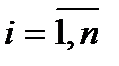. Первые частные производные называются предельными полезностями продуктов. Если 
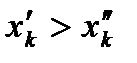при неизменных количествах других продуктов, то 
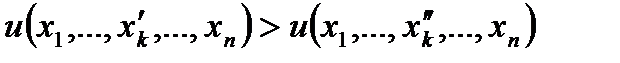. Это означает, что возрастание потребления одного продукта при неизменном потреблении других приводит к росту потребительской оценки. Вектор grad 
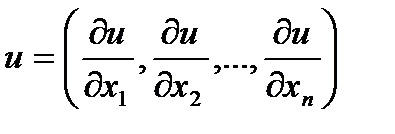функции 
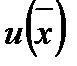показывает направление наибольшего роста функции - вектор предельных полезностей продуктов.
2) 
, 
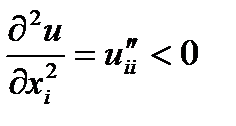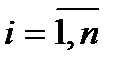, Предельная полезность любого товара уменьшается с ростом его потребления. Это утверждение является законом Госсена (немецкий экономист, первым установивший эту закономерность).
3) 
, 
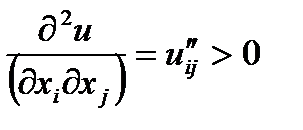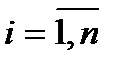. Это свойство означает, что предельная полезность каждого продукта увеличивается с ростом количества другого продукта.
Неоклассическая функция полезности: , , ;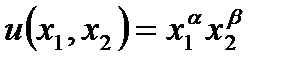
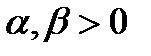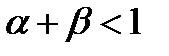Кривые безразличия. В прикладных задачах и моделях потребительского выбора часто используются случай набора из двух товаров. Вводится понятие кривой безразличия, соединяющей потребительские наборы с одним и тем же уровнем удовлетворения. Кривые безразличия представляют собой линии уровня функции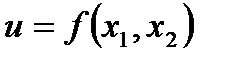 
. Уравнение кривой безразличия: 
.
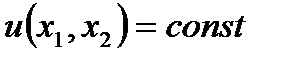Множество кривых безразличия (карта кривых безразличия) изображается на плоскости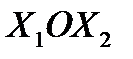 
в виде семейства кривых.
Основные свойства кривых безразличия: 1. Кривые безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются. 2. Кривые безразличия убывают. Первая производная функции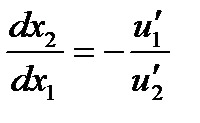 
отрицательна по свойству 1) функции полезности.3. Кривые безразличия выпуклы вниз (рис 1).
Из формул можно получить следующее приближенное равенство: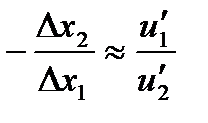 
, которое показывает, на сколько индивид должен увеличить или уменьшить потребление второго продукта при уменьшении или увеличении потребления первого продукта на одну единицу, не изменяя уровня удовлетворения.
3. Бюджетное множество ограничений Множество наборов товаров стоимостью не более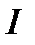 
при данных ценах называется бюджетным множеством 
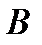, а множество наборов стоимостью 
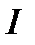называется границей множества 
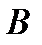и обозначается 
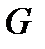. Так как граница 
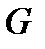определяется соотношением 
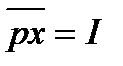, то бюджетное множество 
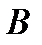описывается системой неравенств в векторной форме: 
, 
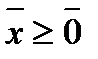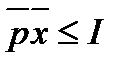, в координатной форме: 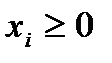, , 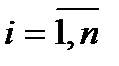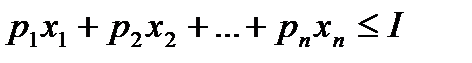. В случае набора из двух товаров бюджетным множеством является треугольник, ограниченный осями координат 
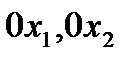и прямой 
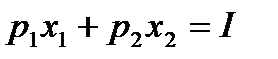(рис. 2).
| X2 |
| X1 |
| Рис. 1 |
| С1 |
| С4 |
| С3 |
| С2 |
| X1 |
| X2 |
| 1/p1 |
| 1/p2 |
| p1x1+p2x2=I |
| Рис..2 |
В методах динамического программирования используется аддитивная целевая функция в виде суммы результирующих показателей по этапам - одни решения приводят к необходимости принимать последующие решения, то есть происходит цепь последовательных решений. Пример: Задача о назначениях:
Директор хочет выбрать на работу помощника-секретаря и имеет возможность испытать 3х кандидатов. Известно, что на прием могут прийти секретари трех уровней квалификации, которым можно присвоить баллы: 1) отличный – 3 балла, 2) хороший – 2 балла, 3) посредственный – 1 балл. Известна статистика рынка секретарей каждой квалификации, определяемая вероятностями: Отл. Р= 0,2; Хор. Р= 0,3; Поср. Р= 0,5.
Если кандидату отказано, то он покидает дирекцию, не ожидая.
По методам динамического программирования начинают анализ с конца.
А). Рассмотрим последний этап. Какую ситуацию получим на III этапе? Т.к. третий секретарь будет обязательно принят, то с учетом вероятностей значение аддитивной целевой оценочной функции в баллах, которую мы получим как математическое ожидание (среднее), будет.
а 3 = 3*0,2 + 2*0,3 + 1*0,5 = 1,7
Б). Вернемся на предыдущий этап II-го шага
На втором этапе, если получим отличного (3 балла) секретаря с вероятностью 0,2 – принимаем на работу; если посредственного (1 балл) с вероятностью этого 0,5, то обязательно продолжим на третьем этапе, если же получим хорошего (2 балла) – вероятность 0,3 и остановимся, то в среднем на 2-м этапе получим:
а 2 = 3*0,2 + 2*0,3 + 1,7*0,5 = 2,05
В). Предыдущий этап – первый. Средний выигрыш, который будет, если на 1-м этапе отл.- принимать, хор.-продолжать, поср.- продолжать будет такой:
а 1 = 3*0,2 + 2,05*0,3 + 2,05*0,5 = 2,24
Т.е. за счет того, что мы испытываем трех кандидатов мы получим дополнительный выигрыш качества: ∆ = 2,24 – 1,7 = 0,54
