Примеры решения задач к контрольной работе

Задача 1. Найти указанные пределы:

a) 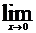; б)

Решение. а) Подстановка предельного значения x= 0 приводит к неопределенности .

Выполним некоторые преобразования и воспользуемся первым замечательным пределом:

= .

б) При основание степени стремиться к 1, а показатель степени 4x+1 стремиться к бесконечности. Следовательно, имеет место неопределенность вида . Представим основание в виде суммы единицы и бесконечно малой величины:

, тогда .

Сделаем замену: . При переменная . Выразим показатель степени через новую переменную. Так как , то 2 x + 3= -4 n, 2 x= -4 n -3,4 x = -8 n - 6.

Таким образом,

(Использован второй замечательный предел.)

Задача 2. Найти производную функции ,

пользуясь правилами и формулами дифференцирования.

Решение. Применив правила дифференцирования суммы, произведения, частного, а так же сложной функции и пользуясь формулами производных элементарных функций, имеем

Задача 3. Исследовать функцию и построить её график по схеме, изложенной в решении.

Решение. 1) Область определения

D(y)= .

2) Исследование на непрерывность и классификация точек разрыва.

Заданная функция непрерывна всюду, кроме точки x=4. Вычислим её односторонние пределы в этой точке:

, .

Таким образом, точка x=4 является для заданной функции точкой разрыва второго рода, а прямая x=4 вертикальной асимптотой.

3) Исследование на экстремум и промежутки монотонности.

- 8x– 20= 0, критические точки:

x		-2
	+		-	не сущ.	-		+
y		-4 max		не сущ.		min

; .

4) Исследование графика на выпуклость, вогнутость, точки перегиба.

Так как , то график заданной функции точек перегиба не имеет. Найдём интервалы выпуклости и вогнутости:

x
	_	не сущ.	+
y		не сущ.

5) Исследование графика на наличие наклонных асимптот.

Таким образом, прямая y= x+4 – наклонная асимптота графика.

6) Строим график на основе полученных результатов.

рис.1

Задача 4. Найти неопределённые интегралы:

а) ; б) ;

в) ; г) .

Решение.

а) Пусть t= arctgx, тогда dt= и .

б) Применим формулу интегрирования по частям:

Пусть u=x, dv= sin(2x-1)dx, тогда du= dx,

;

в) Выделим в числителе производную знаменателя

и преобразуем интеграл:

В интеграле сделаем замену: t= x² +10x +29, тогда dt= (2x+10)dx. Поэтому

Задача 5. Найти объём тела, образованного вращением вокруг оси OX фигуры, ограниченной параболой y= 2x², прямой y= -x+10 и осью OX(рис. 2).

Рис. 2

Решение. Найдём точку пересечения параболы с прямой в первой четверти. Для этого решим систему откуда x=2. Прямая y= -x+ 10 пересекает ось в точке, где x=10. Таким образом, тело ограничено при поверхностью, образованной вращением параболы y= 2x²вокруг оси OX, а при -вращением прямой y= -x+10.

Найдём объём:

(куб.ед.)

Задача 6. Найти частное решение уравнения если y(0)= 4.

Решение. Заменив производную дифференциалом, получим уравнение

Преобразуем его к виду

Затем проинтегрируем обе части:

или

Откуда - общее решение дифференциального уравнения. Подставим в него начальное условие y(0)= 4:

, откуда c= 40

Окончательно, - частное решение дифференциального уравнения.

Задача 7. В вычислительной лаборатории имеются 6 персональных компьютеров фирмы Hewlett-Packardи 4- фирмы IBM. Вероятность того, что во время выполнения некоторого расчёта не произойдёт сбой в компьютере фирмы Hewlett-Packardравна 0,95, а в компьютере IBM- 0,8. Студент производит расчёт на наугад выбранном компьютере. Найти вероятность того, что до окончания расчёта компьютер не выйдет из строя.

Решение. Пусть событие A- компьютер до окончания работы не выйдет из строя. Возможны следующие гипотезы: H₁-студент работал на компьютере фирмы Hewlett-Packard, H₂- студент работал на компьютере фирмыIBM.

Искомую вероятность находим по формуле полной вероятности

Задача 8. Студент с вероятностью 0,1 является отличником. Составить закон распределения числа отличников в группе из 4 наугад выбранных студентов. Найти математическое ожидание и среднее квадратическое отклонение от случайной величины.

Решение. Искомая случайная величина Ч может принимать значения 0, 1, 2, 3, 4. Соответствующие им вероятности найдем по формуле Бернулли