1. Производная от y=x: Dy=Dx Þ Dy/Dx=1 Þ 
y¢=(x)¢=1
2. Производная от константы: y=c, D y =0 для "Dx Þ  Þ, (c)¢=0
Þ, (c)¢=0
3. Производная суммы: y=u+v Þ Dy=Du+Dv Þ  Þ
Þ 
y¢=(u+v)¢=u¢+v¢
4. Производная произведения. y=u×v Þ y+Dy=(u+Du) ×(v+Dv) Þ
Dy=(u+Du)(v+Dv)-u×v=v×Du+u×Dv+Du×Dv, здесь u и v не зависят от D x.
Þ 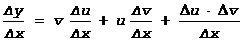 Þ
Þ 
y¢=(u×v)¢=v×u¢+u×v¢, аналогично для любого числа сомножителей.
5. Постоянный множитель выносится за знак производной:
y=c×u, y¢=(c)¢×u+c×u¢=c×u¢ Þ (c×u)¢=c×u¢
6. Производная частного  .
.
 ,
,  Þ
Þ

7. Правило дифференцирования обратной функции.
Как известно, для монотонной на (a,b) y=f(x) существует однозначная обратная функция x=j(y). Если f(x) дифференцируема, то при всех x,при которых f¢(x)¹0, j (y) также дифференцируема, причем
 или
или  или
или 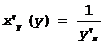 .
.
Эта формула следует из того факта, что:
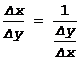
и того, что D x и D y ® 0 одновременно, причем D x¹0 и D y¹0 в силу монотонности. Поэтому

Геометрический смысл.
Обе функции прямая– y=f(x) и обратная – x=j(y) имеют один и тот же график.
y¢x=f¢(x) есть tga,где a - угол, образованный касательной с осью ОХ (касательная в точке (x,y)).
y¢x= tga
Аналогично: x¢y= tgb,где b - угол, образованный той же касательной в той же точке(x,y), но с осью ОУ. Так как a+b=p/2 Þ
tga=1/tgb или tgb=1/tga.
 или
или 
8. Правило дифференцирования сложной функции.
Пусть y=f(z) и z=j(x) -дифференцируемые функции своих аргументов.
Тогда в некоторой области x’, y будет сложной функцией от x Þ y=f(j(x)).
Докажем, что y¢x=(f(j(x)))¢=y¢z×z¢x.
Теорема. Производная от сложной функции y по независимому аргументу x равна производной от y по промежуточному аргументу z,умноженной на его (z) производную по аргументу x.
Доказательство. В силу дифференцируемости y=f(z) по z имеем
 Þ D y =(y¢z+a)Dz,где a -бесконечно малая, Dz®0, то есть
Þ D y =(y¢z+a)Dz,где a -бесконечно малая, Dz®0, то есть
 .
.
Аналогично Dz=(z¢x+b)Dx,где  Þ
Þ
 .
.
Эта теорема справедлива для любого конечного числа суперпозиций функциональных зависимостей. Например:
y=f(z), z=j(u), u=y(v), v=c(x) Þ
y¢x=f¢z×z¢u×u¢v×v¢x.
Все приведенные правила дифференцирования (и особенно последнее)имеют первостепенное значение, так как позволяют находить производные, образованные от любых элементарных функций, образованных при помощи алгебраических действий и наложения функциональных зависимостей. Конечно при условии, что производные основных элементарных функций уже нам известны.
Производные от основных элементарных функций.
1. Показательная функция y=ax.
D x Þ Dy=ax+Dx-ax=ax(aDx-1)
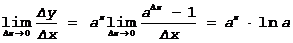 Þ
Þ
y¢=(ax)¢= axlna Þ a=e Þ (ex)¢= ex
2. Логарифмическая функция y=logax.
Здесь сразу можно использовать правило логарифмического обр. функции x=ay Þ и тогда x¢y=ay×lna=xlna,и тогда
 т.к.
т.к. 

При a=e имеем
 .
.
3. Степенная функция y=xn,где nÎR, x>0.
Полагая x=elnx получим y=en×lnx, будем дифференцировать ее как сложную функцию.
4. Функции y=sin x и y=cos x
D y=sin(x+Dx)-sin x=2×sinDx/2×cos(x+Dx/2)

(sin x)¢=cos x
Так как cos x=sin(x+p/2) Þ полагая y=sin z, z=x+p/2 Þ
y¢ = (cos x)¢ = (sin z)¢z×z¢x = cos z = cos (x+p/2) = -sin x.
y¢ = (cos x)¢ = -sin x.
5. tg x и ctg x.

6. Функции y=arcsin x и y=arccos x
а) Так как y=sin x Þ x¢y= cos x=Ö1-sin2y=Ö1-x2,
+, т.к.  и cos y³0 Þ
и cos y³0 Þ 

б) arcsin x + arccos x = p/2 Þ
arccos x = p/2 - arcsin x

7. y= arctg x и y=arcctg x
а) x=tg y, x¢y = sec2y = 1+tg2y = 1+x2


б) Аналогично arctg x + arcctg x = p/2 и

Сводка
Правила
1. x¢=1
2. c¢=0
3. (u+v)¢=u¢+v¢
4. (u×v)¢=u¢×v+v¢×u
5. (c×u)¢=c×u¢
6. 
7. 
8. y=f(z), z=j(x), Þ y¢x=f¢z×z¢x
Формулы
1. (ax)¢= axlna; (ex)¢= ex
2.  ;
; 
3. (xn)¢=n×xn-1
4. (sin x)¢=cos x; (cos x)¢ = -sin x.
5. 
6.  ;
; 
7.  ;
; 
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Примеры:
y=ek×x, y=sin k×x, y=(a×x+b)n, y=Ö1+x2, y=ln sin x,
y=ln(x+Ö1+x2), y=arcsec x, y=sin3x,  ,
,
y=arctg Ölnx, 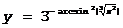
 2018-01-08
2018-01-08 951
951








