Глава 1. Линейное программирование

Краткий курс

МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ В ЭКОНОМИКЕ

П. Конюховский

 

 

УЧЕБНОЕ ПОСОБИЕ

 

Санкт-Петербург

Москва • Харьков • Минск

 

Конюховский П. В.

Математические методы исследования операций в экономике

Серия «Краткий курс»

 

Главный редактор издательства Заведующий редакцией Художественный редактор Литературный редактор Верстка

В. Усманов Л. Волкова В. Земских Е. Маслова Е. Маслова

 

ББК22.183я7+65.529 УДК519.8(075)+658.012.122(075)

 

Конюховский П. В.

К65 Математические методы исследования операций в экономике — СПб.: Издательство «Питер», 2000. — 208 с. — (Серия «Краткий курс»).

 

ISBN 5-8046-0190-3

В настоящем учебном пособии представлены основные разделы исследо­вания операций. Упор делается на изложении теоретических и практических аспектов алгоритмов решения экстремальных задач, которые формулируются на базе известных экономико-математических моделей. Отдельное внимание уделяется вопросам содержательной экономической интерпретации формаль­ных математических понятий.

Серия книг «Краткий курс» предназначена для студентов экономических и управленческих специальностей всех форм обучения, а также для всех инте­ресующихся соответствующей темой.

 

© Конюховский П. В., 2000

© Серия, оформление, ЗАО «Издательство «Питер», 2000

 

Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.

 

ISBN 5-8046-0190-3

 

Издательство «Питер». 196105, С.-Петербург, Благодатная ул., 67. Лицензия ЛР № 066333 от 23.02.99.

Подписано к печати 15.09.99. Формат 60х90/16. Усл. п. л. 13.

Тираж 5000. Заказ 4418.

Отпечатано с фотоформ в АООТ «Типография „Правда”».

119. С.-Петербург, Социалистическая ул., 14.

ПРЕДИСЛОВИЕ

 

Последние годы ознаменовались выходом большого количества книг, посвященных тем или иным разделам экономической науки. Среди них ведущее место, как по количеству наименова­ний так и по тиражу, занимают издания, посвященные финан­сам банковскому делу, теоретическим и практическим вопро­сам управления ценными бумагами. В значительной степени сложившаяся ситуация объясняется острым дефицитом подоб­ной литературы в предыдущие десятилетия. Однако обратной стороной этого несомненно позитивного процесса стало воз­никновение определенного дидактического вакуума вокруг дру­гих экономических тем. Стремление восполнить один из таких пробелов послужило стимулом для выпуска настоящей книги, посвященной основам исследования операции.

Формирование исследования операций как самостоятель­ной ветви прикладной математики относится к периоду 40-х и 50-х годов. Последующие полтора десятилетия были отмечены широким применением полученных фундаментальных теорети­ческих результатов к разнообразным практическим задачам и связанным с этим переосмыслением потенциальных возможно­стей теории. В результате исследование операции приобрело черты классической научной дисциплины, без которой немыс­лимо базовое экономическое образование.

Обращаясь к задачам и проблемам, составляющим предмет исследования операций, нельзя не вспомнить о вкладе, внесен­ном в их решение представителями отечественной научной школы, среди которых в первую очередь должен быть назван Л. В. Канторович, ставший в 1975 г. лауреатом Нобелевской премии за свои работы по оптимальному использованию ресур­сов в экономике.

Предлагаемая вашему вниманию книга задумана как учебное пособие для специалистов в области экономики и управления предприятиями, и призвано создать общее представление о типах задач, изучаемых в исследовании операции, методах их решения и принципиальных идеях, лежащих в основе этих методов. Математические аспекты предмета по отношению к постав­ленным перед настоящим изданием целям не являются перво­степенными. Однако, по мнению автора, попытки излагать те или иные результаты в полном отрыве от математического ап­парата, на основе которого они получены, являются несостоя­тельными и выхолащивающими объективную количественную сторону изучаемых объектов. Поэтому для понимания излага­емого здесь материала от читателя потребуется определенное владение базовыми знаниями из соответствующих разделов ма­тематического анализа и линейной алгебры. Необходимо при­знать, что любая книга экономико-математического направле­ния может быть подвергнута критике либо за чрезмерную перегруженность математическими изысками и оторванность от реальной экономической проблематики, либо за отсутствие математической строгости и корректности, и, естественно, каж­дый автор, исходя из своих вкусов, представлений и умения, ищет оптимальное сочетание того и другого. Ну а о том, на­сколько это удается, судит читатель...

Книга способствует расширению читательского кругозора и помогает ориентироваться среди разделов, задач и методов ис­следования операций. В этой связи многие темы представлены в обзорном ключе.

Несколько замечаний по используемым в ходе изложения условным обозначениям:

¨ ¨ базовые понятия предмета при их первом появлении в тексте выделяются курсивом, а наиболее важные их них (те, кото­рые стоит не забывать и после прочтения!) — жирным шрифтом;

¨ ¨ перед фундаментальными определениями стоит символ F;

¨ ¨ количество приводимых в данной книге теорем минимизиро­вано (это, однако, не должно создать у неподготовленного читателя превратного впечатления об их действительном количестве); в тех местах, где встречается теорема, ее фор­мулировка выделяется слева двойной чертой;

¨ ¨ доказательство теоремы завершается символом A.

 

ВВЕДЕНИЕ

 

Начало развития исследования операций как науки традицион­но связывают с сороковыми годами двадцатого столетия. Среди первых исследований в данном направлении может быть назва­на работа Л. В. Канторовича «Математические методы органи­зации и планирования производства», вышедшая в 1939 г. В за­рубежной литературе отправной точкой обычно считается вышедшая в 1947 г. работа Дж. Данцига, посвященная реше­нию линейных экстремальных задач.

Следует отметить, что не существует жесткого, устоявше­гося и общепринятого определения предмета исследования опе­раций. Часто при ответе на данный вопрос говорится, что «ис­следование операций представляет собой комплекс научных методов для решения задач эффективного управления органи­зационными системами» [14].

Природа систем, фигурирующих в приведенном определении под именем «организационных», может быть самой различной, а их общие математические модели находят применение не толь­ко при решении производственных и экономических задач, но и в биологии, социологических исследованиях и других практи­ческих сферах. Кстати, само название дисциплины связано с применением математических методов для управления военны­ми операциями.

Несмотря на многообразие задач организационного управ­ления, при их решении можно выделить некоторую общую по­следовательность этапов, через которые проходит любое опе­рационное исследование. Как правило, это:

1. Постановка задачи.

2. Построение содержательной (вербальной) модели рассматриваемого объекта (процесса). На данном этапе происходит формализация цели управления объектом, выделение возмож­ных управляющих воздействий, влияющих на достижение сфор­мулированной цели, а также описание системы ограничений на управляющие воздействия.

3. Построение математической модели, т. е. перевод сконст­руированной вербальной модели в ту форму, в которой для ее изучения может быть использован математический аппарат.

4. Решение задач, сформулированных на базе постро­енной математической модели.

5. Проверка полученных результатов на их адекватность природе изучаемой системы, включая исследование влияния так называемых внемодельных факторов, и возможная коррек­тировка первоначальной модели.

6. Реализация полученного решения на практике.

Центральное место в данной книге отведено вопросам, отно­сящимся к четвертому пункту приведенной выше схемы. Это делается не потому, что он является самым важным, сложным или интересным, а потому, что остальные пункты существенно зависят от конкретной природы изучаемой системы, в силу чего для действий, которые должны производиться в их рамках, не могут быть сформулированы универсальные и содержательные рекомендации. По этому поводу, например, X. Таха заметил, что исследование операций одновременно является как наукой, так и искусством [27].

Математическое моделирование в исследовании операций является, сводной стороны, очень важным и сложным, а с дру­гой — практически не поддающимся научной формализации процессом. Заметим, что неоднократно предпринимавшиеся по­пытки выделить общие принципы создания математических мо­делей приводили либо к декларированию рекомендаций самого общего характера, трудноприложимых для решения конкрет­ных проблем, либо, наоборот, к появлению рецептов, примени­мых в действительности только к узкому кругу задач. Поэтому более полезным представляется знакомство с техникой мате­матического моделирования на конкретных примерах.

В качестве таких примеров приведем несколько классиче­ских экономико-математических моделей и задач, которые мо­гут быть сформулированы на их основе.

Управление портфелем активов. Рассмотрим проблему принятия инвестором решения о вложении имеющегося у него капитала. Набор характеристик потенциальных объектов для инвестирования, имеющих условные имена от А до F, задается следующей таблицей.

 

Название	Доходность (в%)	Срок выкупа (год)	Надежность (в баллах)
А	5,5
В	6,0
С	8,0
D	7,5
Е	5,5
F	7,0

Предположим, что при принятии решения о приобретении активов должны быть соблюдены условия:

a) суммарный объем капитала, который должен быть вложен, составляет $ 100 000;

b) доля средств, вложенная в один объект, не может превы­шать четверти от всего объема;

c) более половины всех средств должны быть вложены в дол­госрочные активы (допустим, на рассматриваемый момент к тако­вым относятся активы со сроком погашения после 2004 г.);

d) доля активов, имеющих надежность менее чем 4 балла, не может превышать трети от суммарного объема.

Приступим к составлению экономико-математической моде­ли для данной ситуации. Целесообразно начать процесс с опре­деления структуры управляемых переменных. В рассматривае­мом примере в качестве таких переменных выступают объемы средств, вложенные в активы той или иной фирмы. Обозначим их как х_А, х_В, х_C, х_D, х_Е, х_F. Тогда суммарная прибыль от раз­мещенных активов, которую получит инвестор, может быть представлена в виде

 

 

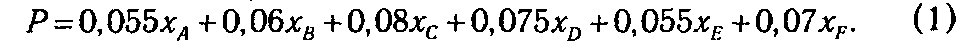
На следующем этапе моделирования мы должны формально описать перечисленные выше ограничения a-d на структуру портфеля.

a) Ограничение на суммарный объем активов:

 

х_A + х_B + х_C + х_D + х_E + х_F ≤ 100 000. (2)

 

b) Ограничение на размер доли каждого актива:

 

х_A ≤ 25 000, x_B ≤ 25 000, x_C ≤ 25 000,

x_D ≤ 25 000, x_E ≤ 25 000, x_F ≤ 25 000. (3)

 

c) Ограничение, связанное с необходимостью вкладывать по­ловину средств в долгосрочные активы:

 

x_B + x_C ≥ 50 000. (4)

 

d) Ограничение на долю ненадежных активов:

 

х_C + х_D ≤ 30 000. (5)

 

Наконец, система ограничений в соответствии с экономиче­ским смыслом задачи должна быть дополнена условиями неот­рицательности для искомых переменных:

 

х_A ≥ 0, х_B ≥ 0, х_С ≥ 0, х_D ≥ 0, х_E ≥ 0, х_F ≥ 0. (6)

 

Выражения (1)-(6) образуют математическую модель поведения инвестора. В рамках этой модели может быть по­ставлена задача поиска таких значений переменных х_A, x_B, x_C, x_D, x_E, x_F, при которых достигается наибольшее значение при­были (т. е. функции (1)) и одновременно выполняются ограничения на структуру портфеля активов (2)-(6).

Перейдем теперь к рассмотрению более общих моделей и задач.

Простейшая задача производственного планирования. Пусть имеется некоторый экономический объект (предприятие, цех, артель и т. п.), который может производить некоторую продукцию n видов. В процессе производства допустимо исполь­зование m видов ресурсов (сырья). Применяемые технологии ха­рактеризуются нормами затрат единицы сырья на единицу произ­водимого продукта. Обозначим через а_i,j количество i -го ресурса (i Î 1: m), которое тратится на производство единицы j -го продук­та (j Î 1:n). Весь набор технологических затрат в производстве j-го продукта можно представить в виде вектора-столбца

 

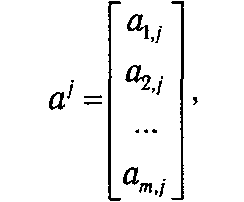
а технологию рассматриваемого предприятия (объекта) в виде прямоугольной матpицы pазмеpности m на n:

 

Если j -й продукт производится в количестве x_j, то в рамках описанных выше технологий мы должны потратить a _{1, j}x_j перво­го ресурса, a _{2, j}x_j — второго, и так далее, a_m,jx_j - m -го. Свод­ный план производства по всем продуктам может быть пред­ставлен в виде n -мерного вектора-строки х = (х₁, х₂,...,х_j,...,х_n). Тогда общие затраты по i -му ресурсу на производство всех про­дуктов можно выразить в виде суммы

 

 

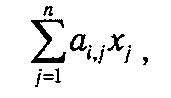
представляющей собой скалярное произведение векторов а^j и х. Очевидно, что всякая реальная производственная система име­ет ограничения на ресурсы, которые она тратит в процессе производства. В рамках излагаемой модели эти ограничения по­рождаются m -мерным вектором b=(b₁, b₂,...,b_m), где b_i — макси­мальное количество i -гo продукта, которое можно потратить в производственном процессе. В математической форме данные ог­раничения представляются в виде системы m неравенств:

 

 

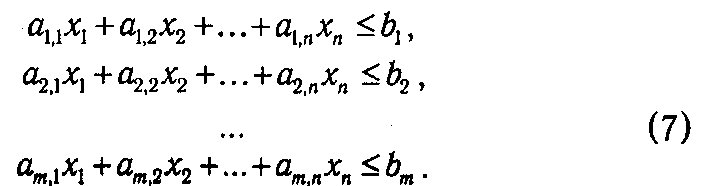
Применяя правила матричной алгебры, систему (7) можно записать в краткой форме, представив левую часть как произве­дение матрицы А на вектор х, а правую — как вектор b:

 

 

К системе (8) также должны быть добавлены естественные ограничения на неотрицательность компонентов плана произ­водства: х ₁ ≥ 0,..., х_j ≥0,.... х_n ≥ 0, или, что то же самое,

 

 

Обозначив через с_j цену единицы j -го продукта, получим вы­ражение суммарного дохода от выполнения плана производства, задаваемого вектором х:

 

 

Формулы (8)-(10) являются не чем иным, как простейшей математической моделью, описывающей отдельные стороны функционирования некоторого экономического объекта, пове­дением которого мы хотим управлять. В рамках данной модели, вообще говоря, можно поставить различные задачи, но, скорее всего, самой «естественной» будет задача поиска такого плана производства х Î Rⁿ, который дает наибольшее значение сум­марного дохода, т. е. функции (10), и одновременно удовлетво­ряет системе ограничений (8)-(9). Кратко такую задачу можно записать в следующем виде:

 

 

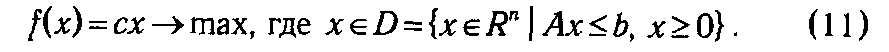
Несмотря на явную условность рассматриваемой ситуации и кажущуюся простоту задачи (11), ее решение является далеко не тривиальным и во многом стало практически возможным только после разработки специального математического аппа­рата. Существенным достоинством используемых здесь мето­дов решения является их универсальность, поскольку к моде­ли (11) могут быть сведены очень многие как экономические, так и неэкономические проблемы.

Поскольку любая научная модель содержит упрощающие предпосылки, для корректного применения полученных с ее по­мощью результатов необходимо четкое понимание сути этих уп­рощений, что, в конечном счете, и позволяет сделать вывод об их допустимости или недопустимости. Наиболее «сильным» уп­рощением в рассмотренной модели является предположение о прямо пропорциональной (линейной) зависимости между объе­мами расхода ресурсов и объемами производства, которая зада­ется с помощью норм затрат а_i,j. Очевидно, что это допущение далеко не всегда выполняется. Так, объемы расхода многих ресурсов (например, основных фондов) изменяются скачкооб­разно в зависимости от изменения компонентов объема про­изводства х. К другим упрощающим предпосылкам относятся предположения о независимости цен с_j от объемов х_j, что спра­ведливо лишь для определенных пределов их изменения, пре­небрежение эффектом кооперации в технологиях и т. п. Данные «уязвимые» места важно знать еще и потому, что они указыва­ют принципиальные направления совершенствования модели.

Транспортная задача. Рассмотрим проблему организации перевозки некоторого продукта между пунктами его производ­ства, количество которых равно m, и n пунктами потребления. Каждый i -й пункт производства (iÎ 1 :m) характеризуется запа­сом продукта а _i ≥ 0, а каждый j-и пункт потребления (j Î 1: n) — потребностью в продукте b_j ≥ 0. Сеть дорог, соединяющая сис­тему рассматриваемых пунктов, моделируется с помощью мат­рицы С размерности m на n, элементы которой с_i,j представля­ют собой нормы затрат на перевозку единицы груза из пункта производства i в пункт потребления j. План перевозки груза в данной транспортной сети представляется в виде массива эле­ментов размерности m х n:

х = (x_1,1…x_1,n, x_2,1….,x_2,n,…, x_i,1, …, x_i,n,…, x_m,1,…,x_m,n). (12)

 

В (12) план перевозок х может рассматриваться как вектор, распадающийся на m групп, по n элементов в каждой, причем i -я группа соответствует объемам груза, вывозимым из j -го пун­кта производства во все возможные пункты потребления. Если реальная перевозка между пунктами i и j отсутствует, то пола­гают х_i,j = 0.

Ограничения на возможные значения х Î R^mn имеют вид:

1. 1. Ограничение на удовлетворение потребностей во всех пун­ктах потребления:

 

 

2. Ограничения на возможности вывоза запасов из всех пун­ктов производства:

 

 

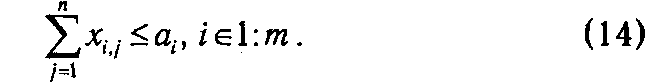
3. Условия неотрицательности компонентов вектора плана:

 

х, х_i,j ≥ 0, i Î l: m, j Î l: n. (15)

 

Существенной характеристикой описываемой модели яв­ляется соотношение параметров а_i и b_j. Если суммарный объем производства равен суммарному объему потребления, а именно,

 

 

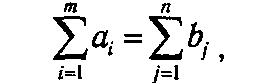
то система называется сбалансированной. При выполнении условия сбалансированности разумно накладывать такие огра­ничения на суммарный ввоз и вывоз груза, при которых полно­стью вывозится весь груз и не остается неудовлетворенных потребностей, т. е. условия (13) и (14) приобретают форму ра­венств.

По аналогии с задачей производственного планирования предположим, что затраты на перевозку прямо пропорцио­нальны количеству перевозимого груза. Тогда суммарные за­траты на перевозку в системе примут вид:

 

Функция (16) и описанные выше ограничения, записанные в форме

 

 

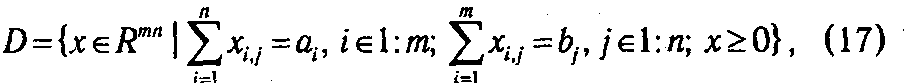
задают транспортную модель. На ее основе может быть сформулирована задача минимизации суммарных затрат на пе­ревозки:

f(x)=cx → min, xÎ D, (18)

 

которая в литературе получила название транспортной зада­чи в матричной постановке. Вообще говоря, транспортная задача является частным случаем задачи (11), но в силу ряда особенностей для ее решения применяются специфические ме­тоды, которые, помимо прочего, позволяют прийти к важным теоретическим обобщениям.

Общим для рассмотренных выше задач является то, что в них стоит проблема поиска наибольшего или наименьшего (оп­тимального) значения некоторой функции, отражающей цель управления системой, или, как еще говорят, целевой функции. Поиск оптимального значения осуществляется на некотором подмножестве допустимых значений переменных, описывающих состояние этой системы, именуемом множеством допустимых планов.

Пусть на некотором множестве D определена функция f(x). Напомним, что точка х*, принадлежащая D (х*Î D), называет­ся точкой глобального максимума, если для любого x Î D выполняется неравенство f(x) ≤ f(x*). В этом случае значение f(x*) называется глобальным максимумом функции. Точ­ка х̀́ называется точкой локального максимума, если су­ществует некоторая окрестность этой точки, в любой точке ко­торой значение функции меньше, чем в х́̀ (f(x) ≤ f(x́̀)). По аналогии, с точностью до знака неравенства, определяются глобальный и локальный минимумы. Обобщающим понятием для максимума и минимума является таксой термин, как эк­стремум (оптимум).

Необходимо отметить, что далеко не всегда весь комплекс целей и задач, стоящий перед моделируемым объектом, может быть выражен в форме некоторой целевой функции. Более того, осознание и осмысление этой проблемы стало своего рода пере­ломным этапом в истории развития исследования операций как науки, положившим конец многим необоснованным ожидани­ям и одновременно давшим толчок к развитию новых направле­ний, связанных с методами многокритериальной оптимизации. Однако следует иметь в виду, что все они базируются на фундаменте методов однокритериальной оптимизации, без ясного понимания которых невозможна работа с более сложным мате­матическим аппаратом.

Как уже отмечалось выше, работа с данной книгой предпола­гает знакомство читателя с классическими методами поиска экст­ремума, основывающимися на аппарате дифференциального исчисления. Но непосредственное применение классических ме­тодов для оптимизации функций, зависящих от большого числа переменных, при наличии значительного количества ограниче­ний наталкивается на серьезные вычислительные трудности, что делает соответствующий аппарат неэффективным.

Мощным инструментом разрешения подобного рода задач стали специальные методы поиска экстремума, составляющие содержание раздела исследования операций, который называ­ется математическое программирование. В данном случае понятие программирование употребляется в смысле планиро­вание (в отличие от программирования для ЭВМ).

В свою очередь, в зависимости от вида решаемых задач, в ма­тематическом программировании выделяют такие области, как линейное, нелинейное, дискретное, динамическое, геомет­рическое, стохастическое программирование. Первые четыре раздела, а также их применение для решения экономических задач составили содержание последующих глав.

 

ГЛАВА 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ