Двойственный симплекс-метод

 

1.7.1. Основные идеи двойственного симплекс-метода. Непосредственное приложение теории двойственности к вы­числительным алгоритмам линейного программирования позво­лило разработать еще один метод решения ЗЛП, получивший название двойственного симплекс-метода, или метода по­следовательного уточнения оценок. Впервые он был предло­жен Лемке в 1954 г.

В процессе изложения идей, положенных в основу двойст­венного симплекс-метода, еще раз воспользуемся второй геометрической интерпретацией ЗЛП. Рассмотрим некоторую КЗЛП (1.48). На рис. 1.11 изображен конус К положительных линейных комбинаций расширенных векторов условий а^j для случая m = 2, n = 6, а на рис. 1.12 — (для большей наглядно­сти) — поперечное сечение данного конуса некоторой плос­костью L, проходящей параллельно оси аппликат.

С каждым планом и задачи, двойственной по отношению к (1.48), можно взаимно однозначно связать гиперплоскость, проходящую через начало координат и перпендикулярную век­тору (-1, и). Допустимые планы двойственной задачи (1.49) должны удовлетворять условиям иА ≥ с, которые можно пере­писать в виде (1, и) А ≥ 0. Последнее означает, что всякий рас­ширенный вектор условий а^j лежит «ниже» плоскости, опреде­ляемой вектором (-1, и). Таким образом, любому допустимому плану двойственной задачи в рассматриваемом примере соот­ветствует некоторая плоскость, расположенная выше всех рас­ширенных векторов, а стало быть, и конуса К. На рис. 1.12, где изображено поперечное сечение, конусу К отвечает многогран­ник, а «гиперплоскостям двойственных планов» — пунктирные линии, являющиеся их следами.

 

 

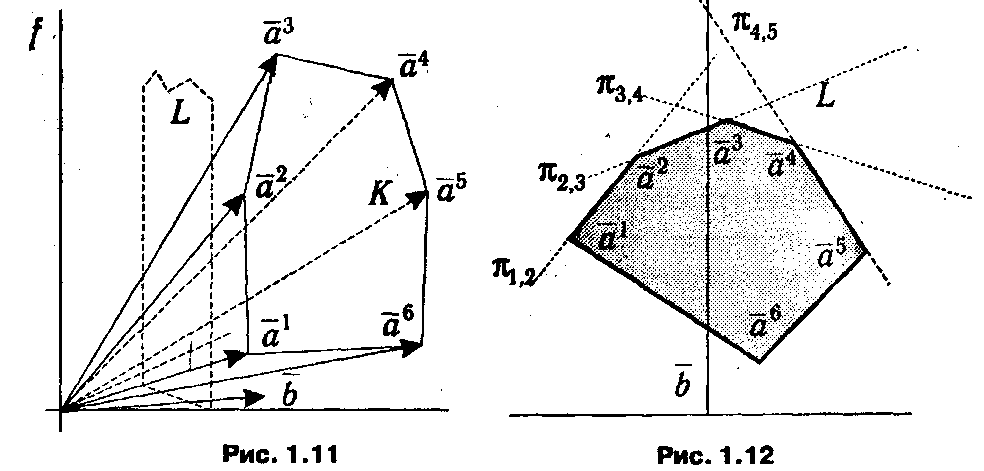
По аналогии с интерпретацией решения прямой задачи про­цесс решения двойственной задачи может быть представлен как поиск такой гиперплоскости, которая лежит выше конуса К и пересекает прямую, проведенную через конец вектора b параллельно оси аппликат, в самой нижней точке.

Из геометрической иллюстрации видно, что плоскости, не соприкасающиеся с конусом К, заведомо не представляют инте­реса, так как для любой из них легко указать плоскость, у кото­рой искомая точка пересечения лежит ниже. Таким образом, процесс поиска экстремума сводится к последовательному пе­ребору плоскостей, касающихся «верхних» граней конуса, или, как еще говорят, опорных по отношению к конусу. Для слу­чая, изображенного на рис. 1.12, таковыми являются гиперплоскости π_1,2, π_2,3, π_3,4 и π_4,5. Как можно заметить, каждая из рассматриваемых гиперплоскостей натянута на некоторый ба­зисный набор расширенных векторов а^j, что, собственно, и ис­пользовано для их обозначения (π_1,2 ~ { а ¹, а ²} и т. д.).

 

F F В дальнейшем систему β={ a^{j 1}, a^{j 2},... ,a^jm } из т линейно-не­зависимых столбцов матрицы условий прямой задачи А будем называть сопряженным базисом, или двойствен­но допустимым базисом, если всякий вектор и Î R^m, удовлетворяющий условиям, удовлетворяет также ус­ловиям иа^j≥c_j(j Î1: n), т. е. является допустимым пла­ном двойственной задачи (1.49).

 

План двойственной задачи и, соответствующий сопряженно­му базису β={ a^{j 1}, a^{j 2},... ,a^jm }, называют опорным планом. Его «опорность» заключается в том, что в системе ограничений uа^j ≥ c_j (j Î1: n), задающих область определения двойственной задачи D *, т неравенств с номерами j Î N (β) обращаются в ра­венства.

Следует обратить внимание на то, что не всем сопряжен­ным базисам соответствуют допустимые базисные планы пря­мой задачи. В частности, вектор b не может быть разложен с неотрицательными коэффициентами по базисам { а ¹, а ²}, { а ³, а ⁴ } или { а ⁴, а ⁵}. В связи с этим систему коэффициентов разложения вектора b по сопряженному базису называют псев­допланом. В то же время базис {а², а³} является допустимым для прямой задачи, и, более того, из иллюстрации видно, что он, с одной стороны, определяет максимум прямой задачи (наивыс­шую точку пересечения прямой, проходящей через конец b, с конусом К), а с другой — минимум двойственной (низшую точ­ку пересечения этой прямой с лежащей над К опорной гипер­плоскостью):

 

 

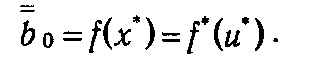
Последний факт является не чем иным, как геометрической иллюстрацией утверждения теоремы 1.5.

Описанные выше свойства пары двойственных задач линейно­го программирования являются идейной основой двойственного симплекс-метода, который представляет собой итеративный про­цесс целенаправленного перебора сопряженных (двойственно допустимых) базисов и соответствующих псевдопланов. В этом и заключено его принципиальное отличие от обычного симп­лекс-метода, в котором последовательно рассматриваются допу­стимые базисные планы прямой задачи*. Нетрудно догадаться, что при определенной структуре задачи путь, предлагаемый двойственным алгоритмом, может оказаться более коротким.

* В данном пункте используется та же система обозначений, что и в п. 1.4.1.

 

F Критерий оптимальности псевдоплана х в двойствен­ном симплекс-методе заключается в том,

что х одновре­менно должен являться допустимым планом прямой задачи, т. е. все его

компоненты должны быть не­отрицательны (х_j ≥ 0).

Обратно, если хотя бы одна из компонент псевдоплана яв­ляется отрицательной, то процесс улучшения значения целе­вой функции может быть продолжен. Геометрическая иллюст­рация данной ситуации приведена на рис. 1.13. Здесь на плоскости (для m = 2) изображена система столбцов ограниче­ний КЗЛП, из которых { а ¹, а ²} образуют текущий базис. Как видно из рисунка, вектор ограничений имеет отрицательную ко­ординату по направлению, задаваемому вектором а ¹. В то же время очевидны и те базисы (например, { а ², а ³}), в которых b будет иметь все положительные координаты. Однако это не все­гда так. Пример на рис. 1.14 иллюстрирует случай отсутствия допустимых планов у прямой задачи: вектор b имеет отрицатель­ную компоненту в текущем базисе { а ¹, а ²} по направлению а ², а для всех остальных небазисных столбцов (а ³, а ⁴) данная коор­дината является положительной, т. е. b и столбцы, являющиеся кандидатами на ввод в очередной базис, лежат в разных полу­плоскостях, образуемых прямой, проходящей через вектор а ¹,

 

 

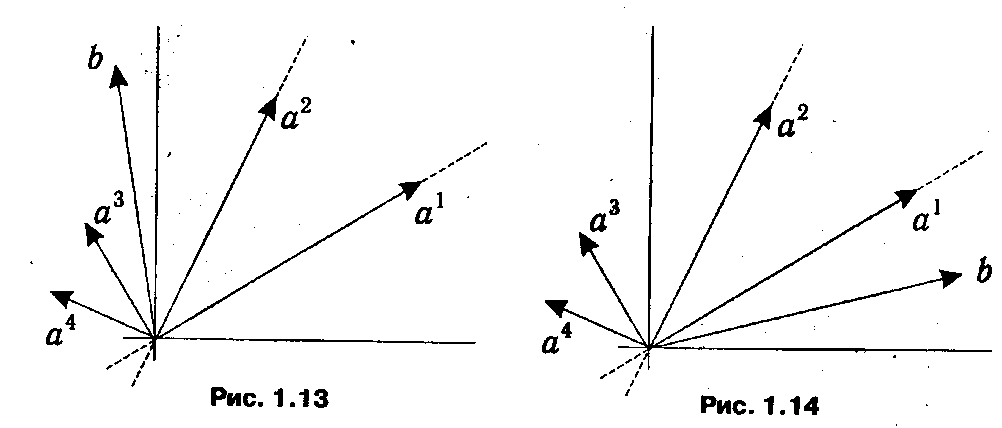
и при любых базисах, отличных от текущего, соответствующая координата вектора b все равно останется отрицательной.

F Таким образом, в двойственном симплекс-методе признаком отсутствия допустимых планов у

решаемой КЗЛП является неотрицательность каких-либо r-х компонент во всех столбцах а^j,

представленных в текущем базисе β (a_r,j (β) ≥ 0, j Î1: n) если b_r (β) < 0 l.*

* Здесь следует подчеркнуть, что двойственный симплекс-метод не­посредственно нацелен на нахождение решения прямой задачи.

 

С другой стороны, если b_r (β)<0 и в строке а_r (β) существуют отрицательные координаты, то псевдоплан можно улучшить выводя из базиса столбец, находящийся на r-м месте, и вводя в него некоторый вектор a^l, имеющий отрицательную r-ую координату. При наличии в векторе b (β) нескольких отрицательных компонент номер вектора, выводимого из базиса, обычно опре­деляется строкой, содержащей наименьшую (наибольшую по модулю и отрицательную) компоненту.

Принцип выбора столбца, вводимого в базис, определяется необходимостью обеспечивать то, чтобы очередной базис опре­делял опорную плоскость, ниже которой располагаются все не­базисные векторы. Для этого требуется, чтобы оценки всех не­базисных векторов а _{0, j} (β) (j Î N (β)), вычисляемые по формулам

 

а _{0, j} (β) = - c_{j +} c (β) а^j (β)

 

(см. (1.26)), оставались положительными. Это, в свою очередь, означает, что номер вводимого столбца l должен быть опреде­лен таким образом. Чтобы

 

 

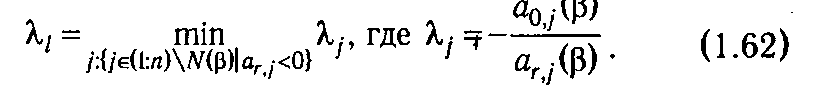
После выбора выводимого и вводимого векторов производит­ся обычный пересчет симплекс-таблицы по формулам, анало­гичным формулам (1.28)-(1.31), и процесс итеративно повто­ряется. В результате через конечное число шагов будет найден оптимальный план КЗЛП или установлен факт пустоты множе­ства допустимых планов.

 

1.7.2. Алгоритм и табличная реализация двойственно­го симплекс-метода. Обобщая сказанное в предыдущем пун­кте, приведем в сжатом виде алгоритм двойственного симплекс-метода для решения КЗЛП.

0-этап. Нахождение исходного сопряженного (двой­ственно допустимого базиса). Результатом 0-этапа являют­ся сопряженный базис β⁽¹⁾ и соответствующие ему псевдоплан x (β⁽¹⁾), матрица A (β⁽¹⁾) и вектор b (β⁽¹⁾), которые будут исполь­зованы на первой итерации. Полагаем номер текущей итерации q равным 1 и переходим к I-этапу.

I-этап. Стандартная итерация алгоритма — выполня­ется для очередного сопряженного базиса β^{( q )}.

1°. Проверка оптимальности текущего псевдоплана: осу­ществляется просмотр значений b_i (β^{( q )}), i Î1: m. Возможны два варианта:

1΄. Для всех i Î1: m, b_i (β^(q)) ≥ 0. Тогда текущий псевдоплан x (β^{( q )}) одновременно является допустимым планом решаемой задачи, т. е. ее оптимальным планом. Вычислительный про­цесс закончен. Элементы оптимального плана х * определяют­ся по формуле

 

 

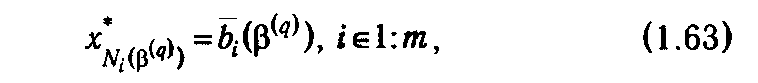
а достигаемое на нем значение целевой функции равно

 

 

1". Существует по меньшей мере один номер строки r Î1: m, для которого b_r (β^{( q )})<0. Следовательно, псевдоплан x (β^(q)) — неоптимален. Выбирается строка с номером r, такая, что

 

 

Она становится ведущей и определяет номер столбца N_r (β^{( q )}), который должен быть выведен из базиса. Переходим к пункту 2° алгоритма.

2°. Определение столбца, вводимого в базис. Рассматрива­ется ведущая строка а_r (β^{( q )}). Возможны два варианта:

2'. Для всех j Î1: n а_r,j (β^{( q )}) ≥ 0. Делается вывод об отсут­ствии допустимых планов у решаемой задачи (D = Ø) и за­вершается вычислительный процесс*.

* Очевидно, что для определения пустоты множества допустимых планов достаточно найти полностью неотрицательную строку а_i (β^{( q )}), соответствующую b_i (β^{( q )}) < 0.

 

2". В строке а_r (β^{( q )}) существует по крайней мере один эле­мент а_r,j (β^{( q )})<0. Согласно правилу (1.62) определяются l — номер столбца, вводимого в очередной базис. Переходим к пун­кту 3° алгоритма.

3°. Пересчет элементов матрицы А и столбца b относи­тельно нового базиса. В соответствии с формулами (1.28)-(1.31) осуществляем расчет элементов матрицы задачи A и век­тора ограничений b относительно нового базиса β^{( q +1)}, который получается в результате вывода из базиса β^{( q )} столбца а^r и вво­да в него столбца а^l. Полагаем номер текущей итерации q: = q+ 1 и переходим к первому пункту алгоритма.

По аналогии со стандартным симплекс-методом вычислитель­ную процедуру двойственного симплекс-метода удобно офор­млять в виде таблиц, приведенных на рис. 1.5. Очевидно, что с формальной стороны их структура остается неизменной. Иног­да считается целесообразным добавить к двойственной симп­лекс-таблице строку, содержащую строку со значениями λ _j, которые вычисляются на этапе определения столбца, вводимо­го в базис.

1.7.3. Особенности применения двойственного симп­лекс-метода. Алгоритм двойственного симплекс-метода (как и остальные симплекс-алгоритмы) предполагает знание исход­ного сопряженного базиса. Очевидно, что в общем случае его нахождение является достаточно непростой задачей, сводящей на нет потенциальные преимущества двойственного алгоритма. Однако в ряде случаев исходный псевдоплан может быть опре­делен достаточно легко.

Рассмотрим задачу минимизации:

 

 

при ограничениях

 

 

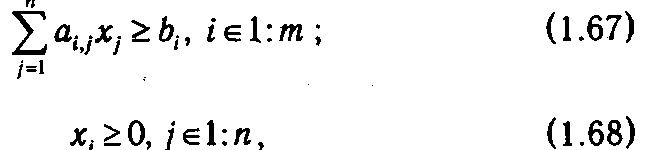
где

 

Приведем задачу (1.66)-(1.68) к канонической форме, введя фиктивные переменные х_{n +1}, х_{n +2}, ..., х_n+m:

 

 

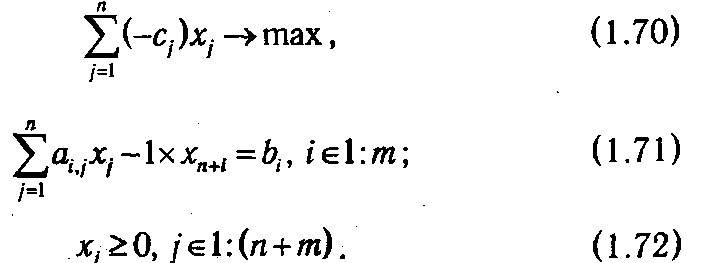
Задача, двойственная к (1.70)—(1.72), будет иметь вид:

 

 

 

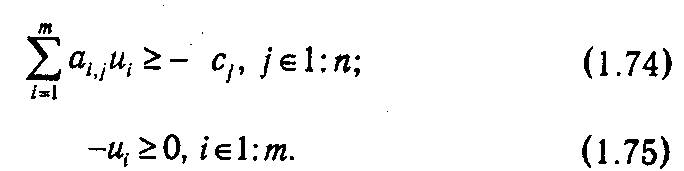
Из (1.74)-(1.75) очевиден допустимый план двойственной задачи

 

 

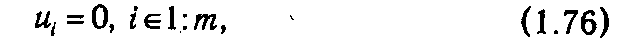
и исходный сопряженный базис, образуемый векторами а^{n+ 1}, а^{n+ 2}, …., а^n+m. При этом начальный псевдоплан равен

 

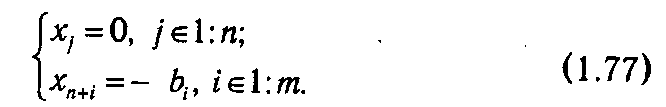
Таким образом, при решении задачи вида (1.66)-(1.68) двой­ственный симплекс-метод имеет несомненные преимущества по сравнению с прямым.

Другое важное направление использования двойственного симплекс-метода связано с поиском оптимальных планов в тех задачах, условия которых претерпели некоторые изменения после того, как они уже были решены с помощью стандартной симплекс-процедуры. Типичными примерами таких изменений являются:

 

Ø Ø изменение компонент вектора ограничений b, что, допу­стим, может быть интерпретировано как корректиров­ка объемов доступных ресурсов в процессе управления экономическим объектом;

Ø Ø добавление новых ограничений к системе условий задачи, что достаточно часто случается при совершенствова­нии используемой экономико-математической модели.

 

В первом случае, т. е. при изменении вектора b, достоинства двойственного симплекс-метода очевидны, так как ранее найден­ный оптимальный базис можно использовать в качестве исход­ного сопряженного базиса при продолжении решения. Второй случай более подробно будет рассмотрен в гл. 4 при рассмотре­нии методов решения целочисленных задач.

В заключение отметим, что в настоящем параграфе был рас­смотрен вариант двойственного алгоритма, соответствующий стандартному симплекс-методу. Нетрудно догадаться, что су­ществует и вариант, построенный на базе модифицированного симплекса (схемы, связанной с преобразованием обратных мат­риц), но, поскольку этот вопрос представляет интерес в основ­ном с точки зрения техники организации вычислений, мы на нем останавливаться не будем. При желании с глубоким и детальным описанием данной версии алгоритма можно ознако­миться в [1]. Отметим лишь, что она обладает теми же прин­ципиальными преимуществами, что и модифицированный симп­лекс-метод.

1.7.4. Пример решения ЗЛП двойственным симплекс-методом. Рассмотрим на конкретном, примере процесс реше­ния КЗЛП двойственным симплекс-методом. Для этого, опять-таки, вернемся к задаче (1.34)-(1.35), решенной в п. 1.4.3 и п. 1.5.2. Предположим, что произошли изменения в векторе ограничений b в результате которых

 

Содержание исходной симплекс-таблицы T ⁽¹⁾ (за исключением столбца b (β⁽¹⁾)) будет идентично содержанию таблицы, полу­чающейся на последнем шаге алгоритма, рассмотренного в п. 1.4.3. Для вычисления значений b (β⁽¹⁾) в данном случае мож­но воспользоваться обратной матрицей, полученной на послед­ней итерации в п. 1.5.2:

 

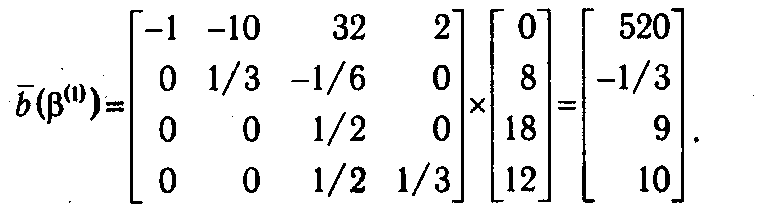
В результате имеем:

 

 

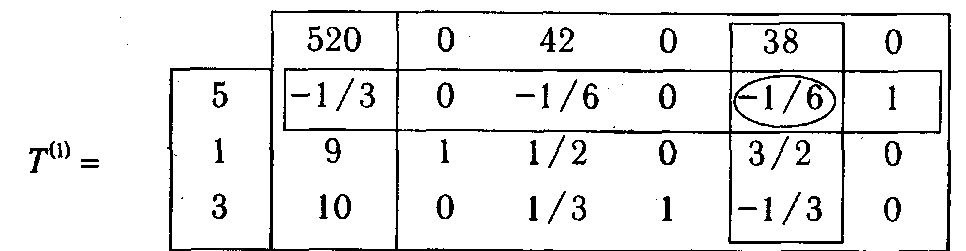
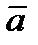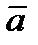Как видно из таблицы Т ⁽¹⁾, в столбце b (β⁽¹⁾) содержатся отрицательные элементы b ₁(β⁽¹⁾) = - 1/3<0), то есть базис β⁽¹⁾ ={ ⁵, ¹, 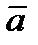³} не является оптимальным, но в то же время легко убедиться, что он обладает свойствами сопряженного базиса. Отрицательный элемент в b (β⁽¹⁾) является единствен­ным, поэтому номер столбца, выводимого из базиса, опреде­ляется однозначно — r = 1 и N ₁(β⁽¹⁾)=5. Далее рассматриваем строку a ₁(β⁽¹⁾) = (0, -1/6, 0, -1/6, 1). В ней имеются отри­цательные элементы. Вычисляем λ₂ =42:(-(-1/6))=252, λ₄ =38:(-(-1/6))=228. λ₂> λ₄, следовательно, номер столбца, вводимого в базис — l = 4. Осуществляем преобразование и получаем симплекс-таблицу T ⁽²⁾.

 

 

Поскольку b (β⁽²⁾) >0, то достигнутый базис N (β⁽²⁾) = {4,1,3} является оптимальным. Из Т ⁽²⁾ можно выписать оптимальный план х * = (6, 0, 32/3, 2, 0) и соответствующее ему значение це­левой функции f (x *)= 444.

КЛЮЧЕВЫЕ ПОНЯТИЯ

 

Ø Ø Общая задача линейного программирования (ОЗЛП).

Ø Ø Каноническая задача линейного программирования (КЗЛП).

Ø Ø Допустимый план.

Ø Ø Оптимальный план.

Ø Ø Первая геометрическая интерпретация ЗЛП.

Ø Ø Базисное решение ЗЛП.

Ø Ø Вторая геометрическая интерпретация ЗЛП.

Ø Ø Вырожденный и невырожденный план ЗЛП.

Ø Ø Симплекс-метод — метод последовательного улучшения плана.

Ø Ø Критерий оптимальности допустимого базисного плана.

Ø Ø Метод минимизации невязок.

Ø Ø Модифицированный симплекс-метод — вычислительная схема, связанная с преобразованием обратных матриц.

Ø Ø Двойственная задача линейного программирования.

Ø Ø Симметричность отношения двойственности.

Ø Ø Теоремы двойственности.

Ø Ø Экономическая интерпретация двойственных оценок.

Ø Ø Параметрическая устойчивость решения ЗЛП.

Ø Ø Двойственный симплекс-метод — метод последовательно­го уточнения оценок.

Ø Ø Сопряженный (двойственно допустимый) базис.

Ø Ø Опорный план и псевдоплан.

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1.1. Сформулируйте задачу линейного программирования.

1.2. Дайте определение для следующих понятий: план, допус­тимый план, оптимальный план,

решение задачи.

1.3. Чем отличается общая задача линейного программирова­ния от канонической?

1.4. Всегда ли общую задачу линейного программирования можно привести к каноническому виду?

1.5. Дайте определения для следующих понятий: аффинное множество, гиперплоскость, базис.

1.6. Чем отличается выпуклый многогранник от многогранно­го выпуклого множества?

1.7. В чем отличие понятий «линейная оболочка» и «выпуклая оболочка»?

1.8. Любой ли конус является выпуклым множеством?

1.9. Какая точка выпуклого множества называется угловой?

1.10. В чем заключается первая геометрическая интерпрета­ция задачи линейного программирования?

1.11. В чем заключается вторая геометрическая интерпрета­ция задачи линейного программирования?

В чем ее отли­чие от первой?

1.12. Какой план называется базисным?

1.13. Как связаны базисные планы и угловые точки области оп­ределения задачи линейного

программирования?

1.14. Какой план задачи линейного программирования называ­ется вырожденным?

1.15. Как с точки зрения второй геометрической интерпрета­ции можно представить процесс поиска

оптимального плана в задаче линейного программирования?

1.16. Сформулируйте критерий оптимальности допустимого базисного плана, применяемый в

симплекс-методе.

1.17. Сформулируйте основные этапы стандартной итерации симплекс-метода.

1.18. Для чего применяется преобразование Жордана—Гаусса?

1.19. Какой элемент симплекс-таблицы называется ведущим?

1.20. При каких условиях делается вывод о неограниченности целевой функции в решаемой задаче?

Какая геометриче­ская интерпретация соответствует данному случаю?

1.21. Можно ли заранее точно определить количество итера­ций, которое потребуется для решения

задачи симплекс-методом? Можно ли найти верхнюю границу для данной величины?

1.22. Какая задача называется вырожденной? По каким призна­кам можно узнать, что текущий план

является вырожден­ным?

1.23. Какие проблемы возникают при решении вырожденных задач?

1.24. Какую экономическую интерпретацию имеет ситуация вырожденности?

1.25. В чем основная идея метода возмущений?

1.26. Для чего предназначен метод минимизации невязок?

1.27. Сформулируйте основные отличия модифицированного симплекс-метода по отношению к

стандартному.

1.28. Перечислите преимущества модифицированного симп­лекс-метода.

1.29. Будет ли отличаться количество итераций при решении одной и той же задачи при решении ее

стандартным и мо­дифицированным симплекс-методом?

1.30. Дайте определение двойственной задачи.

1.31. Какими основными свойствами обладает пара двойствен­ных задач?

1.32. В чем заключается экономическая интерпретация пере­менных двойственной задачи?

1.33. Какой смысл вкладывается в понятие «параметрическая устойчивость»?

1.34. Сформулируйте условия для допустимых изменений це­левой функции задачи, при которых ее

оптимальный план остается неизменным.

1.35. Перечислите основные идеи, на которых базируется алго­ритм двойственного симплекс-метода.

1.36. Дайте определение сопряженного базиса.

1.37. Что такое псевдоплан?

1.38. Сформулируйте критерий оптимальности, используемый в алгоритме двойственного симплекс-

метода.

1.39. По каким признакам можно определить, что множество допустимых планов задачи, решаемой

двойственным сим­плекс-методом, пусто?

1.40. 1.40. В каких ситуациях могут быть реализованы преимуще­ства двойственного симплекс-метода?