1.6.1. Понятие двойственной задачи ЛП. Пусть задана КЗЛП (1.7). Если целевая функция f (x) = cx достигает максимального значения на множестве D, то обоснованным представляется вопрос о том, каким образом можно построить верхнюю оценку для нее. Очевидно, что если через и обозначить некоторый m -мерный вектор, то
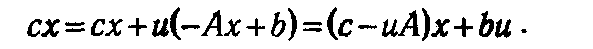
Предположим, что и можно выбрать таким образом, чтобы иА ≥ с. Тогда при любых х ≥ 0 справедливо неравенство

Стремясь получить наилучшую оценку (1.47), мы приходим к формулировке некоторой новой кстремальной задачи, которая в некотором смысле логически сопряжена с задачей (1.7) называется двойственной. Оговоримся, что приведенные рассуждения не носят строгого характера и предназначены только для того, чтобы подготовить читателя к приводимому ниже формальному определению двойственной задачи линейного прoграммирования.
F Если задана каноническая задача ЛП
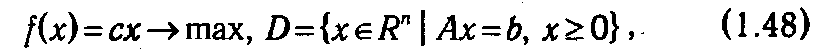
то задача ЛП

называется двойственной по отношению к ней. Соответственно, задача (D, f) no отношению к
|
|
|
(D*,f *) называется прямой (или исходной).
1.6.2. Общая схема построения двойственной задачи. Приведенное выше определение задачи, двойственной по отношению к канонической ЗЛП, может быть распространено на случай общей задачи линейного программирования.
F Если задана общая задача ЛП
f (x) = c 1 x 1 +... + сjхj + сj +1 хj+ 1 +... + сnxn → max, x Î D, (1.50)
где D определяется системой уравнений и неравенств:

то двойственной по отношению к ней называется общая задача ЛП

где D* определяется системой уравнений и неравенств:
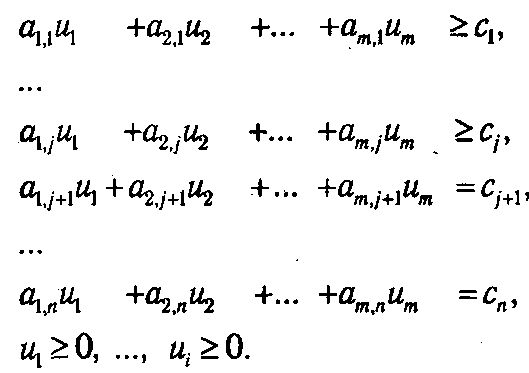
Правила построения задачи, двойственной по отношению к ОЗЛП, наглядно представлены схемой, показанной на рис. 1.9.
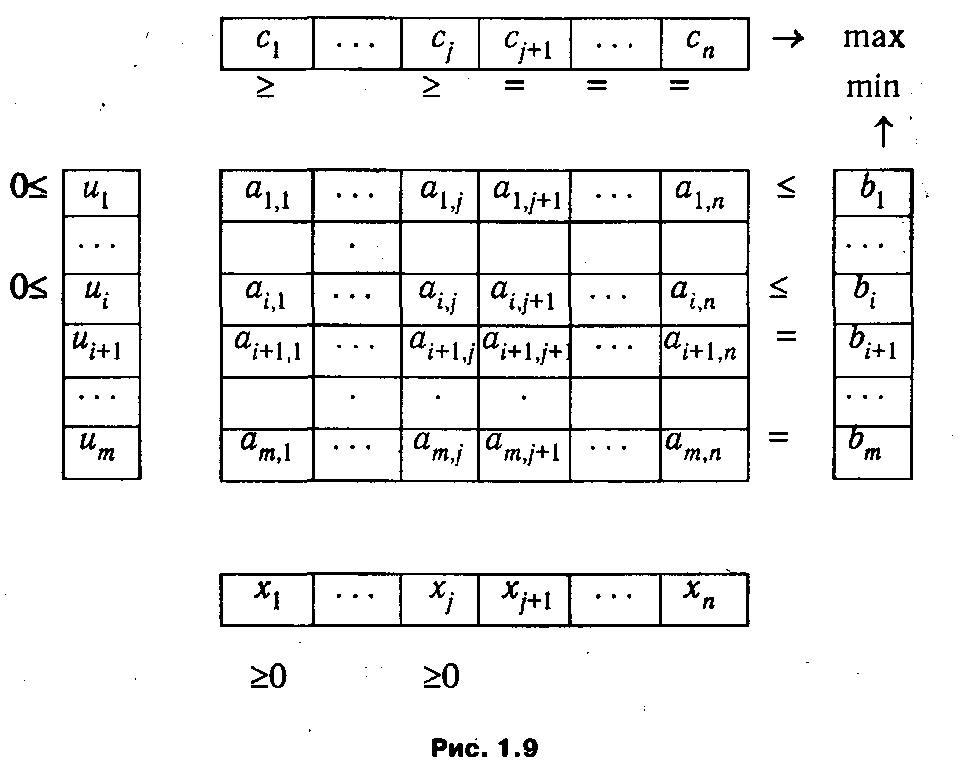
Как следует из приведенной схемы при переходе от прямой задачи ЛП к двойственной:
1. Тип оптимума меняется на противоположный, т. е. максимум на минимум, и наоборот.
2. Вектор коэффициентов целевой функции с и столбец ограничений b меняются местами.
3. Матрица ограничений задачи A транспонируется.
4. Множество индексов переменных, на которые наложено условие неотрицательности в прямой задаче (например, хj ≥ 0 или uj ≥ 0), определяют номера ограничений, имеющих форму неравенств в двойственной задаче (aju ≥ сj или aix ≤ bj).
5. Множество номеров ограничений, имеющих форму неравенств в прямой задаче (например, aix ≤ bj или aju ≥ сj), определяют множество индексов переменных, на которые накладывается условие неотрицательности, в двойственной задаче (ui ≥ 0 или xi ≥ 0).
F F Из приведенного определения вытекает важное свойство — симметричность отношения двойственности, т. е. задача, двойственная по отношению к двойственной, совпадает с прямой (исходной) задачей:
|
|
|
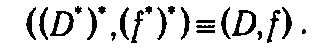
Тем самым имеет смысл говорить о паре взаимно двойственных задач.
В матричной форме пара двойственных общих задач линейного программирования может быть кратко записана как:
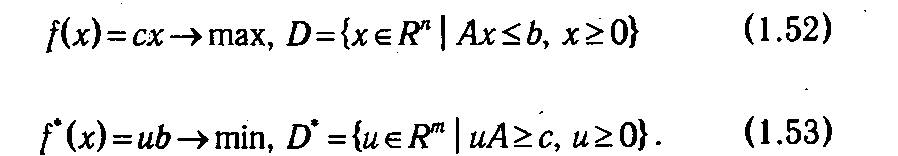
Рассмотрим процесс построения двойственной задачи на конкретном примере. Пусть задана ОЗЛП (D, f):
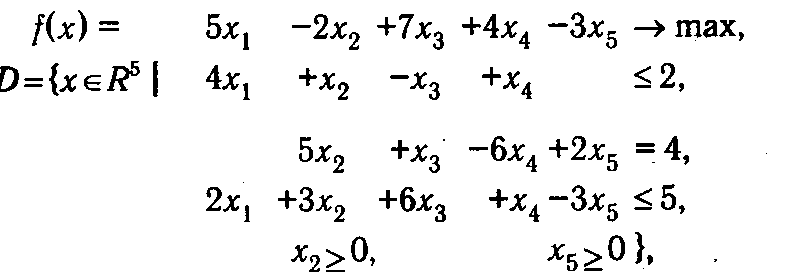
тогда двойственной к ней будет задача (D*, f*):
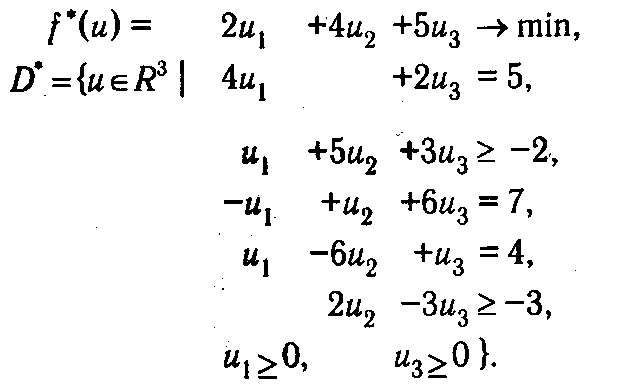
1.6.3. Теоремы двойственности и их применение. Фундаментальные свойства, которыми обладают двойственные задачи линейного программирования, могут быть сформулированы в виде приводимых ниже утверждений. Их обычно называют теоремами двойственности.
| Теорема 1.4. Если х, и— допустимые планы для пары двойственных задач (D,f) и (D*,f*), тo f (x) ≤ f (u). |
Доказательство.
Достаточно доказать теорему для случая, когда задача (D, f) является канонической. Рассмотрим пару двойственных задач
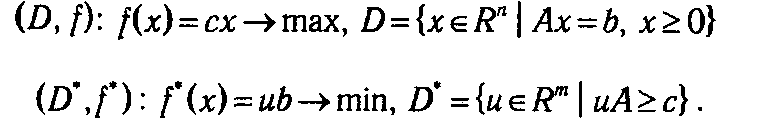
Из того, что вектор и является допустимым планом задачи (D *, f *), следует, что иА ≥ с. Умножив левую и правую части данного неравенства на вектор х ≥ 0, получим равносильную систему неравенств

Одновременно для вектора х, являющегося допустимым планом задачи (D, f), справедливо равенство Ax=b. Тем самым доказано, что иb ≥ сх. A
Замечание. Теорема 1.4, разумеется, верна и для оптимальных планов взаимно двойственных задач: f(x*) ≤ f*(u*), где х* и u*— любые оптимальные планы задач (D, f) и (D*,f *). На самом деле, как будет видно из дальнейшего, справедливо равенство f(x*) = f*(u*).
Теорема 1.5.Если для некоторых допустимых планов 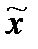 и и 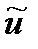 взаимно двойственных задач (D, f) и (D *, f *) выполняется равенство f( взаимно двойственных задач (D, f) и (D *, f *) выполняется равенство f( 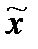 )=f*( )=f*( 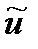 ), то ), то 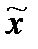 и и 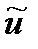 являются оптимальными планами для этих задач. являются оптимальными планами для этих задач.
|
Доказательство.
Согласно теореме 1.4, для всех допустимых планов х задачи (D, f) справедливо неравенство сх < 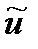 b. По условию теоремы f(
b. По условию теоремы f( 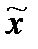 )=f(
)=f( 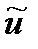 ) или, что то же самое, с
) или, что то же самое, с 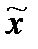 =
= 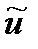 b. Следовательно, верно утверждение: для любого x Î D с
b. Следовательно, верно утверждение: для любого x Î D с 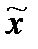 >сх, т. е. х является оптимальным планом для задачи (D, f).
>сх, т. е. х является оптимальным планом для задачи (D, f).
Рассуждения, доказывающие оптимальность плана 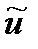 для задачи (D*, f *), проводятся аналогично. A
для задачи (D*, f *), проводятся аналогично. A
| Теорема 1.6.Если целевая функция f в задаче (D, f) не ограничена сверху, то двойственная к ней задача (D*,f*) не имеет допустимых планов. |
Доказательство.
Если предположить, что у двойственной задачи (D *, f *) существует хотя бы один допустимый план и̃, то, согласно теореме 1.4, для любого допустимого плана х задачи (D, f) справедливо неравенство f(x) ≤ f *( 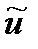 ) <+∞. Последнее означает, что целевая функция f задачи (D, f) ограничена сверху. Поскольку это противоречит условию теоремы, предположение о существовании допустимых планов двойственной задачи (D*,f *) неверно. A
) <+∞. Последнее означает, что целевая функция f задачи (D, f) ограничена сверху. Поскольку это противоречит условию теоремы, предположение о существовании допустимых планов двойственной задачи (D*,f *) неверно. A
Следующее утверждение, известное как теорема равновесия, используется при проверке оптимальности планов ЗЛП.
| Теорема 1.7. Пусть х* и u* — оптимальные планы канонической задачи (D, f) и двойственной по отношению к ней задачи (D*,f*). Если j-я компонента плана х* строго положительна (xj*>0), то соответствующее j-e ограничение двойственной задачи выполняется как равенство: а 1, ju 1* +...+аm,jum*= сj; если же j-й компонент плана х* имеет нулевое значение (хj* =0), то j-e ограничение двойственной задачи выполняется как неравенство: а 1, ju 1* +...+аm,jum*≥ сj. |
Доказательство.
Векторы х* и и*, будучи допустимыми планами соответствующих задач, удовлетворяют условиям: Ах* = b, х* > 0 и и*А-с ≥ 0. Найдем скалярное произведение
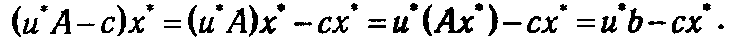
Согласно замечанию к теореме 1.2, оптимальные значения целевых функций взаимно двойственных задач совпадают, т. е. u*b=сх*. Последнее означает, что (u*А-с)х* = 0. Однако скалярное произведение двух неотрицательных векторов может быть равно нулю только в том случае, когда все попарные произведения их соответствующих координат равны нулю. Следовательно, если xj* > 0, то u*аj – сj = 0, если же xj = 0, то возможно u*аj – сj ≥ 0, что и утверждается в теореме. A
|
|
|
Практическое значение теорем двойственности состоит в том, что они позволяют заменить процесс решения основной задачи на решение двойственной, которое в определенных случаях может оказаться более простым. Например, задача, область допустимых значений которой описывается двумя уравнениями, связывающими шесть переменных (m = 2, n = 6), не может быть решена графическим методом. Однако данный метод может быть применен для решения двойственной к ней задачи, которая имеет только две переменные.
Еще раз вернемся к таблице Т 2( q ) (рис. 1.8), получаемой на финальной итерации процедуры модифицированного симплекс-метода. Более подробно рассмотрим нулевую строку матрицы Δ-1(β( q )), для которой было введено обозначение δ0(β( q )). Поэлементно она может быть записана в следующем виде:
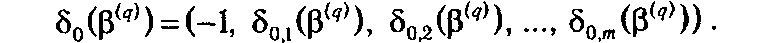
Введем вектор 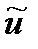 = (δ0,1(β(q)), δ0,2(β(q)),..., δ0, m (β(q))). Нетрудно проверить, что строка оценок a 0(β( q )) может быть представлена следующим образом:
= (δ0,1(β(q)), δ0,2(β(q)),..., δ0, m (β(q))). Нетрудно проверить, что строка оценок a 0(β( q )) может быть представлена следующим образом:
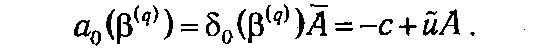
Согласно критерию оптимальности, на последней итерации данная строка неотрицательна, т. е. ũА≥с. Следовательно, вектор и является допустимым планом двойственной задачи.
В то же время элемент b 0(β( q )), содержащий текущее значение целевой функции и равный на последней итерации f(x*), допускает представление
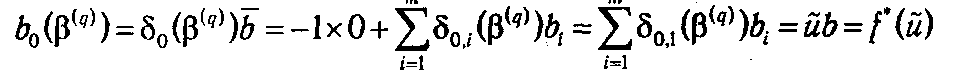
Согласно теореме 1.5 из равенства f (х*) = f *(ũ) вытекает, что вектор ũ служит оптимальным планом двойственной задачи: u = ũ.
Окончательно можно утверждать, что для оптимального базиса
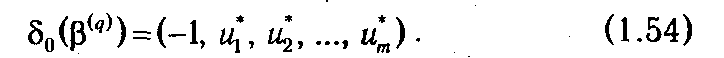
F F Таким образом, существенным преимуществом модифицированного симплекс-метода является то, что он позволяет одновременно найти оптимальные планы как, прямой, так и двойственной задачи.
Читателю в качестве самостоятельного упражнения предлагается построить задачу, двойственную к (1.34)-(1.35), решение которой было приведено в п. 1.5.2, и убедиться, что вектор u = (-10, 32, 2), полученный в таблице Т 2(3), является для нее допустимым и оптимальным планом.
|
|
|
1.6.4. Экономическая интерпретация. Традиционная экономическая интерпретация двойственной задачи ЛП базируется на модели простейшей задачи производственного планирования, описанной во введении. Напомним, что в ней каждый (j -й) элемент вектора х рассматривается как план выпуска продукции данного вида в натуральных единицах, сj — цена единицы продукции j -го вида, аj — вектор, определяющий технологию расходования имеющихся m ресурсов на производство единицы продукции j -го вида, b — вектор ограничений на объемы этих ресурсов.
Предположим, что для некоторых значений A, b и с найден оптимальный план х*, максимизирующий суммарный доход max{ cx }= cx *. Достаточно естественным представляется вопрос: как будет изменяться оптимальный план х * при изменении компонент вектора ограничений b и, в частности, при каких вариациях b оптимальный план х * останется неизменным? Данная задача получила название проблемы устойчивости оптимального плана. Очевидно, что исследование устойчивости х * имеет и непосредственное практическое значение, так как в реальном производстве объемы доступных ресурсов bi; могут существенно колебаться после принятия планового решения х *.
Когда вектор ограничений b изменяется на Δ b или, как еще говорят, получает приращение Δ b, то возникают соответствующие вариации для оптимального плана х*(b+ Δ b) и значения целевой функции f(х *(b+ Δ b)). Допустим, приращение Δ b таково, что оно не приводит к изменению оптимального базиса задачи, т. е. х*(b+ Δ b) ≥0. Определим функцию F (b), возвращающую оптимальное значение целевой функции задачи (D (b), f) для различных значений вектора ограничений b

Рассмотрим отношение ее приращения F(b+ Δ b)-F(b) к приращению аргумента Δ b. Если для некоторого i устремить Δ bi → 0, то мы получим
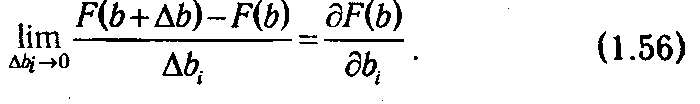
Учитывая, что в соответствии с теоремой 1.5
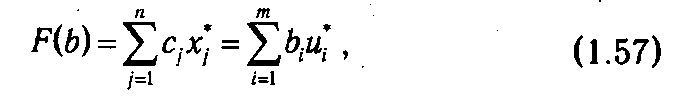
и подставив (1.57) в (1.56), приходим к выражению
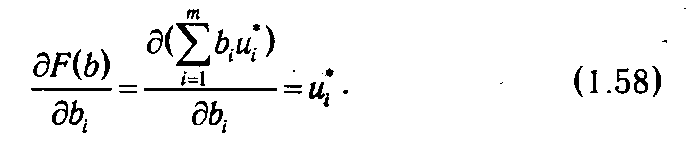
F F Из формулы (1.58) вытекает экономическая интерпретация оптимальных переменных двойственной задачи. Каждый элемент ui* может рассматриваться как предельная (мгновенная) оценка вклада i -го ресурса в суммарный доход F при оптимальном решении х *. Грубо говоря, величина ui* равна приросту дохода, возникающему при увеличении ресурса i на единицу при условии оптимального использования ресурсов.
В различных источниках компоненты оптимального плана двойственной задачи также называются двойственными оценками или теневыми ценами, а Л. В. Канторович предлагал такой термин, как объективно обусловленные оценки.
На основе теорем двойственности для пары задач ЛП в общей форме могут быть сформулированы некоторые важные (с точки зрения экономической интерпретации) следствия.
F F Если при использовании оптимального плана прямой задачи i-e ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей двойственной переменной равно нулю, т.е. если
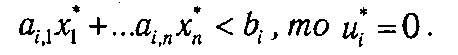
В рамках рассматриваемой задачи производственного планирования это означает, что если некоторый ресурс bi, имеется в избыточном количестве (не используется полностью при реализации оптимального плана), то i -e ограничение становится несущественным и оценка такого ресурса равна 0.
F F Если при использовании оптимального плана двойственной задачи j-e ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей переменной прямой задачи должно быть равно нулю, т. е. если a 1, ju 1* +...аm,j иm – сj > 0, то хj* = 0.
Учитывая экономическое содержание двойственных оценок u 1*,..., um, выражение а 1, ju 1* +… am,jum* может быть интерпретировано как удельные затраты на j -й технологический процесс. Следовательно, если эти затраты превышают прибыль от реализации единицы j -го продукта, то производство j -го продукта является нерентабельным и не должно присутствовать в оптимальном производственном плане (xj* =0).
Несмотря на возможные аналогии, которые могут возникнуть у читателей, знакомых с такими фундаментальными понятиями экономической теории, как предельные издержки и предельный доход, двойственные оценки не следует однозначно отождествлять с ценами (хотя такие попытки иногда предпринимались на начальной стадии становления исследования операций как науки). Еще раз подчеркнем, что переменные двойственной задачи по своему смыслу являются оценками потенциальной возможности получения дополнительной прибыли за счет увеличения соответствующего ресурса в условиях оптимального функционирования управляемого экономического объекта.
1.6.5. Анализ параметрической устойчивости решений ЗЛП. В предыдущем пункте мы затронули некоторые аспекты чувствительности и устойчивости оптимального плана по отношению к изменению вектора ограничений b. Очевидно, что аналогичные вопросы могут быть поставлены для случая вариации коэффициентов целевой функции сj, j Î1: n.
С точки зрения экономической интерпретации задача исследования параметрической устойчивости может быть рассмотрена как изучение тех пределов колебания цен на продукцию управляемого предприятия (фирмы), при которых принятый план выпуска продукции продолжает оставаться оптимальным.
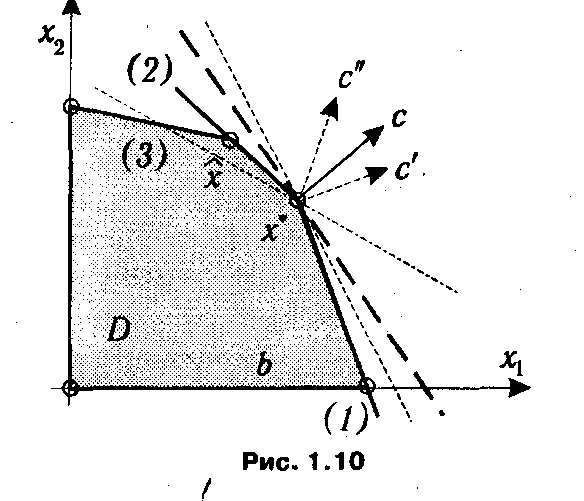
Также содержание проблемы устойчивости оптимального плана ЗЛП по отношению к вариациям целевой функции может быть проиллюстрировано с помощью первой геометрической интерпретации. На рис. 1.10 изображено множество допустимых планов D некоторой задачи ЛП. Как видно из рисунка, целевая функция f (ее поведение отражает линия уровня, показанная жирным пунктиром) достигает экстремального значения в точке х *, а изменению ее коэффициентов от с к с' или с" на рисунке соответствует поворот линии уровня относительно х *. Активным, т. е. обращающимся в равенство, ограничениям в точке х * соответствуют линии (1) и (2). До тех пор, пока при повороте, вызванном изменением вектора с, линия уровня целевой функции не выходит за пределы образуемого линиями ограничений конуса, х* остается оптимальным планом. Как показано на рис. 1.10, этот план не меняется при переходе от с к с', и, наоборот, при переходе от с к с" линия уровня целевой функции f(x)=c"x пересечет линию (2), что вызовет изменение оптимального базисного плана, которым теперь станет точка  .
.
Используя условия оптимальности плана ЗЛП
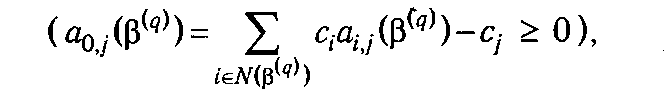
нетрудно получить количественные оценки для пределов колебаний коэффициентов целевой функции, при которых не происходит изменение оптимального плана. Допустим, вариации подвергся некоторый элемент сr : сr′ = сr + εr. Возможны два случая:
1. Столбец r не входит в оптимальный базис (r Î N (β( q ))). Тогда для неизменности оптимального плана необходимо и достаточно выполнение условия
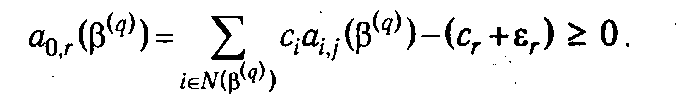
Отсюда можно получить значение для допустимой вариации

2. Столбец r входит в оптимальный базис (r Î N (β( q ))). В этом случае для сохранения оптимальности текущего плана потребуется выполнение для всех небазисных столбцов (j Ï N (β( q ))) условий

Следовательно, в этом случае допустимая вариация должна удовлетворять условиям
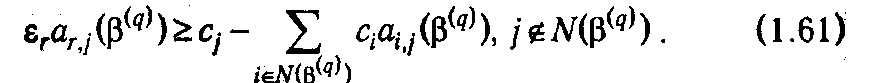
Приведенный пример исследования чувствительности оптимального плана по отношению к изменению параметров задачи является весьма простым. Очевидно, что существуют и более сложные задачи, в которых, например, исследуются совместные вариации параметров разных типов. Они составляют предмет специального раздела исследования операций, получившего название параметрического программирования. Заинтересованный читатель может получить дополнительную информацию по данному предмету в [1, 6].
 2018-01-08
2018-01-08 2242
2242








