Логическая эквивалентность и логическое следствие

Ø Определение. Формулы 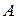и 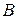называются логически эквивалентными тогда и только тогда, когда формула 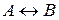– тавтология.

v Теорема. Отношение лог.эквивалентности- отношение эквивалентности (Рефлексивно,симметрично,транзитивно)

Справедливы правило подстановки и правило замены.

Пусть и – формулы, содержащие букву 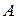, и – формулы, полученные из формул и соответственно подстановкой вместо буквы 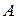формулы .

Правило подстановки. Если формула логически эквивалентна формуле , то формула логически эквивалентна формуле .

Пусть – формула, в которой выделена некоторая подформула , – формула, полученная из формулы заменой на некоторую формулу .

Правило замены. Если формулы и логически эквивалентны, то логически эквивалентны и формулы и .

Доказательства правил подстановки и замены основано на сравнении таблиц истинности соответствующих формул.

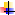Пример.

Док-ем:По правилу подстановки, эквивалентна формуле .

По правилу замены, эквивалентна формуле .Следовательно, по свойству транзитивности, формулы и логически эквивалентны.

Ø Определение. Говорят, что формула 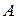логически влечет формулу 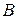, если формула 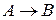является тавтологией.

v Теорема. Отношение логического следствия - отношение предпорядка, то есть рефлексивно и транзитивно.

 

Контрольные вопросы

1. Что изучает формальная логика?

2. Что изучает математическая логика?

3. Изложите основные этапы развития логики.

4. Области применения математической логики.

5. Перечислите известные парадоксы, основные идеи.

6. Разновидности силлогизмов и модусов: отличие и сходство

7. Что такое высказывание?

8. Какие высказывания бывают?

9. Какие высказывания называются простыми, а какие

10. сложными?

11. Что не является высказыванием?

12. Основные логические операции и их свойства, перечислите.

13. Отрицание высказывания. Конъюнкция двух высказываний. Дизъюнкция двух высказываний.

14. Импликация двух высказываний. Эквивалентность двух высказываний.

15. Союзы языка и логические операции (язык и логика). Общий взгляд на логические операции.

16. Конструирование сложных высказываний.

17. Понятие формулы алгебры высказываний.

18. Классификация формул алгебры высказываний.

Глава 3 Задачи регрессионного анализа

 

В практике экономических исследований очень часто имеющие данные нельзя считать выборкой из многомерной нормальной совокупности. В этих случаях пытаются определить поверхность, которая дает наилучшее приближение к исходным данным. Соответствующие методы приближения получили название регрессивного анализа. В регрессивном анализе рассматривается односторонняя зависимость случайной зависимой переменной от одной (или нескольких) неслучайной независимой переменной . Две случайные величины и могут быть связаны либо функциональной зависимостью, либо статистической, либо быть независимыми.

При функциональной зависимости каждому значению переменной соответствует вполне определенное значение переменной . Строгая функциональная зависимость реализуется редко, т.к. обычно величины подвержены еще действию различных случайных факторов. Тогда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной. Это статистическая (вероятностная, стохастическая) зависимость.

Корреляционной зависимостью между двумя случайными величинами, называется функциональная зависимость между значениями одной из них условным математическим ожиданием другой.

Ø Определение У равнения регрессии - уравнения вида , ,

где , - функциями регрессии, а их графики - линиями регрессии.

Рассмотрим двумерную случайную величину , где и - зависимые случайные величины. Представим величину - в виде линейной функции :

,

где и - параметры, подлежащие определению.

Это можно сделать различными методами, наиболее употребительный из них – метод наименьших квадратов.

Функцию называют наилучшим приближением в смысле метода наименьших квадратов, если математическое ожидание принимает наименьшее возможное значение. Функцию называют линейной среднеквадратической регрессией на .

¨ Теорема Линейная среднеквадратическая регрессия на имеет вид

,

где , , , , -коэффициент корреляции величин и .

Коэффициент - коэффициент регрессии на , а прямая называется п рямой среднеквадратической регрессии на .

Аналогично можно получить прямую среднеквадратической регрессией на :

.

Если коэффициент корреляции , то обе прямые регрессии совпадают.

Для отыскания уравнений регрессии необходимо знать закон распределения двумерной случайной величины .

На практике обычно располагают выборкой пар значений ограниченного объема. В этом случае речь может идти об оценке функции регрессии по выборке.

В качестве оценок условных математических ожиданий, принимают условные средние, которые находят по выборочным данным.

Мы рассмотрим линейную регрессию, уравнение которой

,

где - выборочный коэффициент регрессии на . Выборочный коэффициент регрессии показывает, на сколько в среднем изменяется переменная при увеличении переменной на одну единицу.

Условным средним называют среднее арифметическое наблюдавшихся значений , соответствующих .

Например, если при величина приняла значения , то условное среднее .

Ø Определение Уравнения

или

называются выборочными уравнениями регрессии, и - выборочными функциями регрессии, а их графики - выборочными линиями регрессии.

 

3.1 Метод наименьших квадратов

 

Обычно для получения уравнения выборочной линии регрессии рассматривается функция

или

используется метод наименьших квадратов.

Рассмотрим линейную регрессию, уравнение которой

.

Неизвестные параметры и выбираются таким образом, чтобы

Методом наименьших квадратов находим значения коэффициентов и

.

Угловой коэффициент можно представить как

где - выборочный коэффициент корреляции,

, .

- выборочный коэффициент регрессии на .

Выборочный коэффициент регрессии показывает, на сколько в среднем изменяется переменная при увеличении переменной на одну единицу.

 

3.2 Линейный регрессионный анализ

 

Термином линейный регрессионный анализ обозначают прогнозирование одной переменной на основании другой, когда между этими переменными существует линейная взаимосвязь

.

Разности между фактически полученными значениями и вычисленными по уравнению регрессии соответствующими значениями прогнозов называются отклонениями . Величины прогноза являются моделируемыми значениями данных, а отклонения показывают отличия от модели.

Пример Анализ зависимости между ценами и объемам продаж молока фермера. Значение выборочного коэффициента корреляции .

Уравнение регрессии

Задачами регрессионного анализа являются:

· установление формы зависимости между переменными;

· оценка функции регрессии;

· оценка неизвестных значений (прогноз значений) зависимой переменной.

В регрессионном анализе рассматривается односторонняя зависимость случайной зависимой переменной от одной (или нескольких) независимой переменной .

· также называется функцией отклика, выходной, результирующей, эндогенной переменной; - входной, объясняющей, предсказывающей, предикторной, экзогенной переменной, фактором, регрессором.

Линейная зависимость может быть представлена в виде модельного уравнения регрессии

.

В силу воздействия неучтенных случайных факторов отдельные наблюдения будут в большей или меньшей степени отклоняться от функции регрессии

.

В этом случае уравнение взаимосвязи двух переменных (парная регрессионная модель) может быть представлено в виде .

Отклонения (возмущения, остатки) предполагаются независимыми и нормально распределенными . Неизвестными параметрами являются , и .

Оценкой модели по выборке является уравнение регрессии .

Параметры этого уравнения и определяются по методу наименьших квадратов. Воздействие случайных факторов и ошибок наблюдений определяется с помощью остаточной дисперсии .

Оценкой дисперсии является выборочная остаточная дисперсия :

,

где - значение , найденное по уравнению регрессии; - выборочная оценка возмущения . Число степеней свободы , т.к. две степени свободы теряются при определении двух параметров и .

 

3.3 Оценка модели регрессии

 

Величина называется стандартной ошибкой оценки и демонстрирует величину отклонения точек исходных данных от прямой регрессии.

Поскольку, как правило, требуется, чтобы прогноз был как можно более точным, значение должно быть как можно меньшим.

Пример Для данных продажи молока . Для величины , принимающей значения от 3 до18, значение довольно велико.

Чтобы получить точечный прогноз, или предсказание для данного значения , надо просто вычислить значение функции регрессии в точке .

Пример Фермер хочет получить прогноз количества молока, которое будет продано при цене 1.63 рублей за литр:

Конечно, реальные значения величины не лежат в точности на регрессионной прямой. Есть два источника неопределенности в точечном прогнозе, использующем уравнение регрессии.

1. Неопределенность, обусловленная отклонением точек данных от выборочной прямой регрессии.

2. Неопределенность, обусловленная отклонением выборочной прямой регрессии от регрессионной прямой генеральной совокупности.

Интервальный прогноз значений переменной можно построить так, что при этом будут учтены оба источника неопределенности.

Суммарная дисперсия

,

где - стандартная ошибка прогноза, - стандартная ошибка оценки, - стандартная ошибка функции регрессии.

Величина измеряет отклонение выборочной прямой регрессии от регрессионной прямой генеральной совокупности и вычисляется для каждого значения как.

.

зависит от значения , для которого прогнозируется величина . Величина будет минимальна, когда , а по мере удаления от , будет возрастать.

Стандартная ошибка прогноза

Границы интервала прогноза величины с надежностью будут равны , где статистика имеет распределение Стьюдента с степенями свободы.

Госсет Уильям Сит (псевд. Стьюдент)(1876-1937)- английский математик и химик. Труды по теории вероятностей и математической статистике.

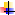Пример Найдем стандартную ошибку прогноза в точке с надежностью .

Ранее было получено , , .

.

При значение .

Находим интервал прогноза или

Построенные аналогичным образом интервалы значений прогноза по всем значениям имеют вид:

Интервал прогноза очень велик, это связано с тем, что исходная выборка мала, а значение сравнительно велико.

Прогноз значений зависимой переменной по уравнению регрессии оправдан, если значение объясняющей переменной не выходит за диапазон ее значений по выборке (причем тем более точный, чем ближе к ).

Экстраполяция кривой регрессии, т.е. использование вне пределов обследованного диапазона значений объясняющей переменной может привести к значительным погрешностям.

Интервал прогноза очень велик, это связано с тем, что исходная выборка мала, а значение сравнительно велико.

 

 

3.4 Проблемы применения метода линейной регрессии

 

1. Если истинная взаимосвязь не линейная, нельзя использовать для прогноза прямую линию. Большинство компьютерных программ не предупреждают об этом.

 

2. Экстраполяция за пределы имеющихся данных потенциально опасна. Вы не располагаете информацией, чтобы отбросить другие возможности.

3.Резко отклоняющееся значение может серьезно повлиять на результаты регрессионного анализа.

4. Большое значение имеет то, какая из двух переменных прогнозируется, а какая служит основанием для прогноза. Каждому из этих подходов соответствует своя линия регрессии. Две линии регрессии сближаются, когда уменьшается фактор случайности точки данных приближаются к прямой линии.

 

3.5 Предпосылки статистической модели ЛР

 

1.Зависимая переменная есть величина случайная, а объясняющая переменная - величина неслучайная.

2. Математическое ожидание возмущения , дисперсия . Возмущения являются нормально распределенными. Для заданного значения генеральная совокупность значений имеет нормальное распределение относительно регрессионной прямой совокупности.

На практике приемлемые результаты получаются и тогда, когда значения имеют нормальное распределение лишь приблизительно.

3. Разброс генеральной совокупности данных относительно регрессионной прямой совокупности остается постоянным всюду вдоль этой прямой (дисперсия зависимой переменной остается постоянной: ).

4 Возмущения , а, следовательно? и значения независимы между собой.

Уравнение взаимосвязи двух переменных (парная регрессивная модель) может быть представлена

где - случайная переменная, характеризующая отклонение от функции регрессии. - называют возмущением.

Рассмотрим линейный регрессивный анализ, для которого функция линейна

Если для оценки параметров линейной функции взята выборка, то парная линейная регрессионная модель имеет вид

 

3.6 Задачи регрессионного анализа

 

Цель регрессионного анализа состоит в определении общего вида уравнения регрессии, построении статистических оценок неизвестных параметров, входящих в уравнение регрессии и проверке статистических гипотез о регрессии.

Корреляционный анализ позволяет устанавливать неслучайность (значимость) изменения наблюдений и степень их зависимости от случайных величин .

Регрессионный анализ представляет собой следующий этап статистического анализа.

Определяются точные количественные характеристики изменения . Статистическая связь и сводится к строгим (неслучайным) соотношениям.

На данном этапе решаются следующие основные задачи:

Ø выбор общего вида функции регрессии

Ø отбор, если необходимо, наиболее информативных факторов;

оценивание параметров уравнения регрессии

Ø анализ точности полученного уравнения регрессии, связанный с построением доверительных интервалов для коэффициентов регрессии, т.е. компонент вектора , для условного среднего отклика и для прогнозов наблюдений отклика при значениях факторов .

1. Возмущения есть случайная величина, а объясняющая переменная – неслучайная величина.

2. Математическое ожидание возмущения равно нулю

3. Дисперсия возмущения постоянна для любого :

4. Возмущения не коррелированны (независимы) ; .

5. Возмущения есть нормально распределенная случайная величина.

Для получения уравнений регрессий достаточно 1-4 условий, 5 условие для оценки точности уравнений регрессии и его параметров

Пусть требуется исследовать зависимость , величины и измеряются в одном эксперименте.

Восстановим по результатам измерений. Точное представление невозможно. Будем искать приближенную зависимость по методу наименьших квадратов. ,

- называется наилучшим приближением, если принимает наименьшее значение.

Рассмотрим функцию которая наилучшим образом приближает к .

Введем обозначения , , , - корреляционный момент, k- коэффициент корреляции этих величин.

Будем искать

Найти такие и , что принимает наименьшее значение:

Исследуем на экстремум

=

=

Коэффициент - коэффициент регрессии. Прямая – прямая регрессии.

Воздействие неучтенных факторов и ошибок наблюдений в модели определяется с помощью остаточной дисперсии.

Минимум равен – остаточная дисперсия, которая характеризует величину ошибки, допускаемой при использовании приближенного равенства .

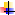Пример Найти выборочное уравнение прямой линии регрессии: а) на , б) на , если известны: выборочные средние , , выборочные дисперсии , , выборочный коэффициент корреляции .

Решение

а) Выборочное уравнение прямой линии регрессии на имеет вид

,

где , .

Поскольку , ,

получаем уравнение

,

или

.

б) Согласно выборочному уравнению прямой линии регрессии на :

.

Поэтому получаем

,

или

 

3.7 Многомерная нормальная регрессионная модель

 

Когда одна случайная переменная реагирует на изменение другой изменением своего закона распределения, речь идет о так называемой стохастической связи.

Частный случай такой связи - когда условное математическое ожидание одной случайной переменной является функцией значения, принимаемого другой случайной переменной, т.е.

,

где - теоретическая (истинная) функция или модель регрессии относительно .

Статистические связи исследуются по выборкам ограниченного объема. На основании этих данных выполняют поиск подходящих аппроксимаций функции .

Чтобы выяснить, как значение одной случайной переменной, в среднем, изменяется в зависимости от того, какие значения принимает другая случайная переменная, используют условное среднее значение , которое является выборочной оценкой условного математического ожидания, а соответствующее выражение - эмпирической функцией регрессии.

Практическое значение знания регрессионной зависимости между случайными переменными и заключается в возможности прогнозирования значения зависимой случайной переменной , когда независимая случайная переменная принимает определенное значение.

Прогноз не может быть безошибочным, однако можно определить границы вероятности ошибки прогноза.

 

 

3.8 Вариация зависимой переменной

 

Рассмотрим вариацию (разброс) значений относительно среднего значения

= .

Обозначим предсказанные с помощью функции регрессии значения

: .

= означает величину разброса, которая обусловленарегрессией (ненулевым значением наклона ).

= означает разброс за счет случайных отклонений от функции регрессии.

Оказывается,

,

- полный разброс равен сумме разбросов за счет регрессии и за счет случайных отклонений.

Величина – это доля вариации значений , обусловленной регрессией (т.е. доля закономерной изменчивости в общей изменчивости).

Ø Определение Коэффициент детерминации – статистика

показывающая, какая доля дисперсии результативного признака объясняется влиянием объясняющих переменных.

Если , это означает, что регрессия ничего не дает, т.е. знание 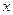не улучшает предсказания для y по сравнению с тривиальным .

Другой крайний случай означает точную подгонку: все точки наблюдений лежат на регрессионной прямой.

Чем ближе к 1 значение , тем лучше качество подгонки. Линейная регрессия имеет следующие общие свойства:

Чем ближе значение коэффициента детерминации к 1, тем ближе модель к эмпирическим наблюдениям.

С увеличением количества объясняющих переменных увеличивается R2.

Контрольные вопросы

 

1. Что показывает коэффициент регрессии?

2. Что показывает коэффициент корреляции?

3. В чем отличие корреляционной зависимости от функциональной?

4. Каким методом определяются параметры линейной регрессии?

5. При каких значениях коэффициента регрессии зависимость случайных величин является:

а) прямой;

б) обратной?

6. Чем занимается регрессионный анализ?

7. Перечислите свойства линейной регрессии.

8. Запишите уравнение регрессии.

9. Отчего зависит наклон линии регрессии?

10. Что показывает коэффициент детерминации?

11. В чем отличие многомерной от линейной регрессии?

 

 

Глава 4 Общая постановка и виды задач принятия решений

 

При проектировании любых технических объектов, технологических процессов и систем всегда решаются задачи выбора и принятия решений.

Задачей принятия решения называют кортеж (совокупность)

,

где – множество вариантов решения задачи;

– принцип оптимальности, дающий представление о качестве вариантов, в простейшем случае – это правило их предпочтения друг перед другом.

Решением задачи принятия решений называется множество , которое является подмножеством множества , полученное на основе принципа оптимальности.

Задачи принятия решений классифицируются по наличию информации об и и бывают трех видов:

1. и – неизвестны. Это общая задача принятия решений. Данные для получения x_опт определяют в данной задаче в процессе ее решения.

2. – неизвестно, – известно (эта задача поиска вариантов).

3. и – известны (это задача оптимизации).

В общем случае задача принятия решения решается в два этапа:

1 этап: Задача формализуется, т.е. строится ее математическая модель, в которой конкретные физические, технические, технологические, экономические условия и требования к объекту воплощаются в виде задачи оптимизации с определенной целевой функцией и допустимым множеством вариантов.

2 этап: Решение задачи оптимизации с использованием известных методов.

 

Основы теории оптимизации

Теория оптимизации, с одной стороны, является самостоятельной наукой, а, с другой стороны, составной частью науки под названием «исследование операций».

Операция (в данной науке) – это совокупность взаимосогласованных действий, направленных на достижение вполне определенной цели.

Обязательно должно быть сформулирована цель. Если есть разные пути достижения этой цели, то необходимо найти наилучший из них.

4.1 Математическая постановка задачи оптимизации

 

Постановка задачи оптимизации включает в себя множество допустимых решений и числовую функцию , определенную на этом множестве, которая называется целевой функцией.

Нельзя отождествлять критерий (критерии) оптимальности и целевую функцию.

Целевая функция – это аналитическая зависимость между критерием (критериями) оптимальности и подлежащими оптимизации параметрами с указанием направления экстремума.

Отличие понятий «критерий» и «целевая функция» состоит в следующем:

1. Целевая функция может включать в себя более одного критерия.

2. Для целевой функции всегда и обязательно указывается вид экстремума:

.

Различают два вида задач оптимизации:

1. Задачу минимизации.

2. Задачу максимизации.

Чтобы решить задачу минимизации функции на множестве , необходимо найти такой вектор (а также соответствующее значение целевой функции ), чтобы неравенство: выполнялось для всех . При этом называют оптимальным решением (точнее здесь – минимальным решением),а - оптимумом (минимумом).

Чтобы решить задачу максимизации функции на множестве , необходимо найти такой вектор (а также соответствующее значение целевой функции ), чтобы неравенство: выполнялось для всех . При этом называют оптимальным (максимальным) решением, а – оптимумом (максимумом).

В общем виде находится именно вектор , т.к., например, при решении двухпараметрической задачи, он будет включать в себя два параметра, трехпараметрической – три параметра и т.д.

 

4.2Локальный и глобальный минимум ЦФ

 

При решении задач оптимизации следует иметь в виду, какой вид имеет целевая функция.

Например, . Целевая функция имеет вид

Здесь т. - глобальный минимум, а т. - локальный минимум целевой функции.

Пусть теперь , здесь - точка глобального максимума, а - точка локального максимума целевой функции.

 

Разрешимость задач оптимизации

Приведенная выше задача оптимизации имеет решение не при любых целевых функциях и допустимых множествах. Существуют задачи, в которых невозможно найти оптимальное решение и экстремум целевой функции. Например, не существует точек минимума функции одной переменной на множестве в случаях, приведенных ниже

Иллюстрация случая, когда множество допустимых решений не замкнуто.

Здесь граница «а» множества допустимых решений в интервал входит, а граница «b» нет. - множество не замкнуто, следовательно, – не существует.

Иллюстрация неограниченности множества допустимых решений

определена лишь одна левая граница множества допустимых решений. , т.е. множество допустимых решений неограниченно.

Рассмотрим, когда задача оптимизации не имеет однозначного решения.

Функция f(x) не является непрерывной,функция не является непрерывной, т.к. в т. существуют два значения функции – и .

Следовательно, задача оптимизации разрешима, если выполняются следующие три условия:

1. Множество допустимых решений замкнуто, т.е. если предельные точки принадлежат этому множеству.

2. Множество ограничено.

3. Целевая функция непрерывна.

Это нестрогая формулировка теоремы Вейерштрасса

 

4.3 Методы безусловной оптимизации

 

Среди методов оптимизации нулевого порядка в САПР находят применение методы Розенброка, конфигураций, деформируемого многогранника, случайного поиска. К методам с использованием производных относятся методы наискорейшего спуска, сопряженных градиентов, переменной метрики.

Метод Розенброка является улучшенным вариантом покоординатного спуска.

 

4.4 Метод покоординатного спуска

 

Метод покоординатного спуска характеризуется выбором направлений поиска поочередно вдоль всех координатных осей, шаг рассчитывается на основе одномерной оптимизации, критерий окончания поиска , где — заданная точность определения локального экстремума, — размерность пространства управляемых параметров. Траектория покоординатного спуска для примера двумерного пространства управляемых параметров показана на рис. 1, где — точки на траектории поиска, — управляемые параметры.

Целевая функция представлена своими линиями равного уровня, около каждой линии записано соответствующее ей значение . Очевидно, что есть точка минимума.

При использовании метода покоординатного спуска велика вероятность "застревания" поиска на дне оврага вдали от точки экстремума. После попадания в точку , расположенную на дне оврага, дальнейшие шаги возможны лишь в направлениях или , но они приводят к ухудшению целевой функции. Следовательно, поиск прекращается в точке .

Оврагом называют часть пространства управляемых параметров, в которой наблюдаются слабые изменения производных целевой функции по одним направлениям и значительные изменения с переменой знака — по некоторым другим направлениям.

Знак производной меняется в точках, принадлежащих дну оврага.

"Застревание" покоординатного спуска на дне оврага

В то же время при благоприятной ориентации дна оврага, а именно при положении одной из координатных осей, близком к параллельности с дном оврага, поиск оказывается весьма быстрым.