Неопределенный интеграл и основные способы интегрирования

Учреждение образования

«ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»

кафедра математики и физики

 

 

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ОСНОВНЫЕ СПОСОБЫ ИНТЕГРИРОВАНИЯ

 

КОНСПЕКТ ЛЕКЦИЙ

 

по дисциплине

«ВЫСШАЯ МАТЕМАТИКА»

 

 

для студентов заочной формы обучения уровня ССО

всех специальностей

 

 

Минск 2006

 

Составитель Т.К. Гресюк

 

Рецензент Е.Н. Ермаш

 

Издание утверждено на заседании кафедры М и Ф

18 мая 2006 года, протокол №10

 

 

Зав. кафедрой Л.Л. Гладков

Начиная изучение темы «Неопределенный интеграл» необходимо хорошо изучить темы:

1) «Понятие о производной функции»;

2) «Формулы дифференцирования»;

3) «Дифференциал функции».

 

Повторим предыдущий материал, с которым тесно связана новая тема по следующим вопросам:

1) Имея функцию, можно ли найти ее производную?

Ответ: можно, по известным формулам дифференцирования.

2) Можно ли по данному закону движения тела найти его скорость?

Ответ: можно, скорость – это есть производная пути по времени (механический смысл производной).

3) По данному уравнению кривой можно ли найти угловой коэффициент касательной, проведенный к этой кривой?

Ответ: можно, применяя знание геометрического смысла производной.

4) Можно ли по данной функции найти дифференциал?

Ответ: можно .

5) С помощью какого действия мы решали все эти четыре задачи?

Ответ: дифференцированием.

6) Что называется дифференцированием?

Ответ: математическое действие, с помощью которого по данной функции находим ее производную, или ее дифференциал, или по данному закону движения тела находим скорость его, или по данному уравнению кривой определяем угловой коэффициент касательной, проведенной к этой кривой, и т.п. называется дифференцированием.

7) Какое условие в этом действии является исходным, и что получаем, применяя данное действие?

Ответ: исходным условием является функция, а получаем или производную, или дифференциал, или скорость, или угловой коэффициент.

Однако часто приходится решать и обратную задачу: по известной скорости движения тела установить закон его движения, по данному угловому коэффициенту касательной к кривой находить уравнение этой кривой и т.п., иначе говоря, по данной производной отыскивать функцию, от которой произошла эта производная.

Заметим, что находить функцию можно не только по данной ее производной, но и по ее дифференциалу, так как производная функции и ее дифференциал связаны простым соотношением

; .

Практически же отыскивать функцию удобнее по ее дифференциалу, поэтому в дальнейшем изложении мы и будем пользоваться дифференциалом для решения обратной задачи.

Возьмем несколько функций

;

;

;

, где .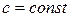

Дифференциал, каждой из них один и тот же

.

Решим обратную задачу: по данному дифференциалу найти саму функцию.

Этому дифференциалу соответствует множество функций, отличающихся свободным членом.

Чтобы решение обратной задачи записать письменно, необходимо ввести кое-какие новые понятия.

Пусть функция

, (1)

имеет производную , тогда ее дифференциал

. (2)

Функция по отношению к ее дифференциалу называется первообразной.

Определение 1. Первообразной функцией для выражения называется функция , дифференциал которой равен .

Однако дифференциалу функции соответствует не единственная первообразная (как мы уже видели), а их множество, причем они отличаются друг от друга постоянным слагаемым.

Так нашему дифференциалу

соответствует множество первообразных функций вида , где – любая постоянная.

Выражение называется неопределенным интегралом для дифференциала и обозначается , то есть .

Определение 2. Совокупность всех первообразных функций для дифференциала называется неопределенным интегралом и обозначается .

Таким образом, можно записать

,

где – знак интеграла;

– подынтегральное выражение;

– произвольная постоянная интегрирования;

– совокупность первообразных функций;

– подынтегральная функция.

Процесс нахождения первообразной функции называется интегрированием, а раздел математики, занимающийся вопросами, связанными с интегрированием – интегральным исчислением.

Из сказанного видно, что интегрирование есть действие обратное дифференцированию.

Определение 3. Математическое действие, с помощью которого по данной производной, или дифференциалу находится сама функция, или по известной скорости движения тела устанавливаем закон его движения, или по данному угловому коэффициенту касательной к кривой находим уравнение этой кривой и т.п. называется интегрированием ( – знак интегрирования).

Теперь вы познакомились с новым математическим действием, которому название интегрирование.

С геометрической точки зрения неопределенный интеграл представляет собой семейство интегральных кривых, каждая из которых получается из любой кривой параллельным переносом вдоль оси (рис. 1)

Рис. 1

График какой-либо первообразной функции называется интегральной кривой.

Если функция непрерывна на некотором промежутке, то на этом промежутке она и интегрируема, то есть существует .

Итак, вы знаете уже десять математических действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, логарифмирование, потенцирование, дифференцирование и интегрирование.

Каждое действие применяется при решении определенной задачи.

В каждом действии свои исходные данные и получается свой конечный результат.

Перед тем, как приступать к выполнению того или иного действия необходимо знать определенные законы, свойства, которым подчиняется это действие.

Вот сейчас мы рассмотрим основные свойства неопределенного интеграла.

Пусть функция является первообразной для функции на некотором промежутке , то есть , .

По определению .

Первое свойство. Производная неопределенного интеграла равна подынтегральной функции, то есть

.

Второе свойство. Дифференциал неопределенного интеграла равен подынтегральному выражению, то есть

Это свойство следует из определения неопределенного интеграла

,

если

,

то есть

.

Третье свойство. Неопределенный интеграл от дифференциала некоторой функции равен этой функции, сложенной с произвольной постоянной

.

Пусть .

Если возьмем интеграл от обеих частей этого равенства, то получим

.

Но по определению

,

следовательно

.

Примем без доказательства еще следующие свойства неопределенного интеграла.

Четвертое свойство. Постоянный множитель можно выносить за знак интеграла, то есть

,

где - постоянный множитель.

Пятое свойство. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от каждой из них, то есть

.

Для нахождения неопределенного интеграла еще необходимо знать основные формулы интегрирования.

1 (по второму свойству)

2 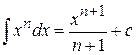- интеграл степени.

Докажем верность этого равенства.

Рассмотрим функцию и найдем ее дифференциал

.

Взяв интеграл от обеих частей этого равенства, получим

.

Применяя второе свойство интеграла к левой части последнего равенства и третье свойство к правой части, найдем

,

отсюда, при имеем

.

Обозначив постоянное слагаемое буквой , будем иметь окончательно

.

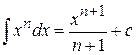Выведенная формула справедлива для любого значения 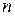, кроме . В последнем случае формула теряет смысл.

3

Докажем верность этого равенства.

Зададимся вопросом, какая функция имеет своим дифференциалом выражение .

Такой является функция , так как

,

следовательно,

.

4 (легко получается, если применить формулы дифференцирования).

5

Докажем это равенство.

По определению неопределенного интеграла имеем

,

,

.

Следовательно, записанное равенство (5) верно.

 

Далее запишем формулы, легко получаемые из формул дифференцирования.

6

7

8

9

10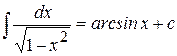

11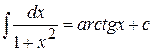

Зная определение неопределенного интеграла, свойства неопределенного интеграла и основные формулы интегрирования, можно решать примеры и задачи с применение действия интегрирования.