Парная линейная регрессия

Вид уравнения и предпосылки для регрессионного анализа

Парная линейная регрессия описывается уравнением:

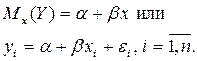
Для получения оценки параметров линейной функции регрессии взята выборка, состоящая из векторных переменных (x_i, y_i).

Оценкой записанной выше модели является уравнени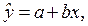е где

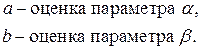
Классический подход к оцениванию параметров α и β основан на классическом (обычном или традиционном) методе наименьших квадратов (МНК).

Чтобы регрессионный анализ давал достоверные результаты необходимо выполнить 4 условия Га­усса - Маркова:

1. M (ε_i) = 0 – остатки имеют нулевое среднее для всех i = 1,…, n.

2. D (ε_i) = σ² = const для всех i = 1,…, n – гомоскедастичность остатков, то есть их равноизменчивость.

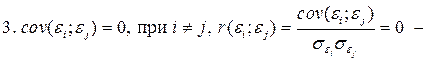
– отсутствие автокорреляции в остатках.

4. Объясняющая переменная X детерминирована, а объясняемая переменная Y – случайная величина и остатки не коррелируют с X:

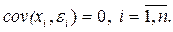
Объясняющая переменная в том случае, когда она стоит в уравнении регрессии, может называться регрессором.

Наряду с этими четырьмя условиями Гаусса - Маркова применяют 5-е условие: остатки должны быть распределены нормально; это условие необходимо для обеспе­чения правильного оценивания значимости уравнения регрессии и его параметров.

Наилучшие оценки называют BLUE – оценками (Best Linear Unbiased Estima­tors).

Они обладают следующими свойствами:

1. Это оценки несмещённые:

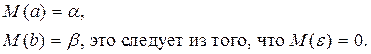
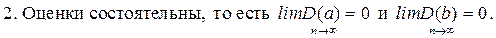
3. Оценки эффективны, то есть имеют наименьшие дисперсии среди всех воз­можных оценок.

Если нарушаются 2-е и/или 3-е условия Гаусса – Маркова, то оценки не теряют свойства 1и 2, а свойство 3 (эффективность) теряют; дисперсии становятся смещёнными.

Отыскание оценок параметров парной регрессии

Сущность МНК для парной регрессии состоит в минимизации суммы квадратов остатков (ESS – Error Sum of Squares).

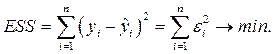
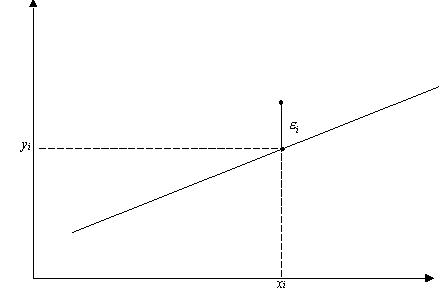
Наблюдаемое значение 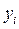, положение модельной точки 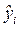на линии регрессии и остаток 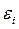показаны на приведеном ниже рис. 3.1.

y

x

рис. 3.1

Учитывая, что параболы второй степени имеют один экстремум, отыщем ста­ционарную точку ESS, как функции двух переменных a и b:

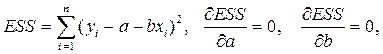
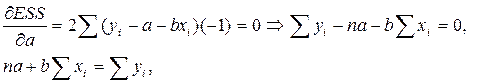
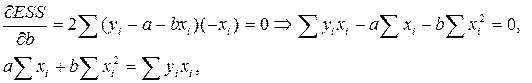
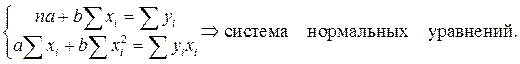
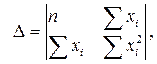
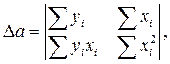
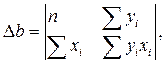
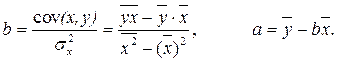
Параметр b – это коэффициент регрессии. Его величина показывает, на сколько единиц собственного измерения изменяется результат Y, при изменении фактора на одну единицу собственного измерения;

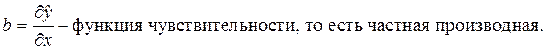
Свободный член a показывает совокупное влияние на результативный признак факторов, не учтённых в модели.

Уравнение регрессии почти всегда дополняют показателем тесноты статистиче­ской связи между случайными величинами X и Y. Для парной линейной регрессии это будет линейный коэффи­циент корреляции:

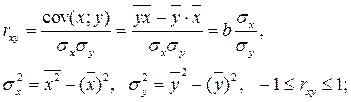
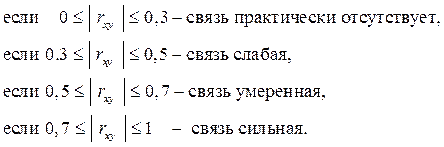
Корреляционная зависимость между двумя переменными – это функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.

Коэффициент r_xy оценивает тесноту связи рассмотренных при­знаков в её линейной форме, поэтому близость r_xy к нулю не всегда означает отсутст­вие связи между признаками. При другой (нелинейной, специальной модели) связь между признаками может оказаться тесной.

Для оценки качества подбора линейных функций также рассчитывают коэффициент детерминации 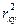. Он характеризует долю дисперсии признака Y, объясненную рег­рессией, в общей дисперсии.

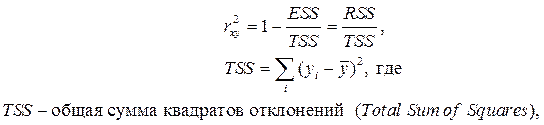
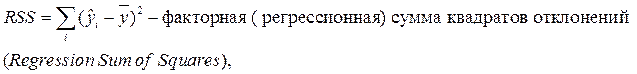
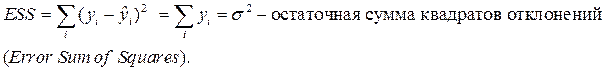
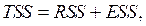
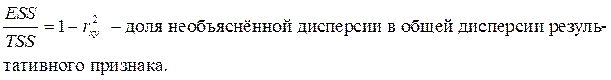
Оценка значимости уравнения и его параметров

После того как уравнение линейной регрессии построено, производится оценка значимости уравнения в целом и отдельных его параметров.

Значимость уравнения в целом оценивается по значению (величине) F –стати­стики Фишера. При этом выдвигается основная гипотеза 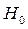о том, что коэффициент регрессии b равен нулю и фактор X не влияет на результат Y.

Для расчёта F используют дисперсии на одну степень свободы; такие диспер­сии сравнимы между собой по величине, так как приведены к общей шкале.

df – число степеней свободы (degrees of freedom),

df _TSS = n ­­­­ – 1, то есть свободно могут варьироваться n – 1 отклонений, а n- е отклонение может быть вычислено по этим отклонениям и среднему значению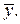

При заданном объёме наблюдений величина RSS в парной регрессии зависит от одной константы, а именно от коэффициента регрессии b, то есть RSS имеет одну степень свободы.

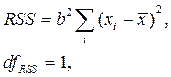
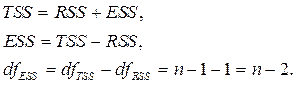
Дисперсии на одну степень свободы для парной регрессии обозначаются так:

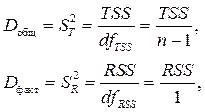
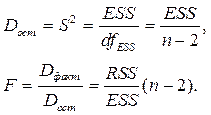
По таблице Фишера – Снедекора, содержащей критические значения F при раз­ных уровнях γ существенности нулевой гипотезы и разных df, найдём F_{к р} (критическое значение) для конкретной задачи:

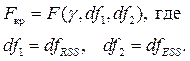
Если расчётное значение F > F_кр, то H ₀ отклоняется и связь между X и Y призна­ётся существенной, а уравнение признается адекватным. Если F < < < F_кр, то уравнение признается неадекватным.

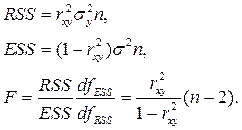
В линейной регрессионной модели оценивают значимость не только уравнения в целом, но и отдельных его параметров. Для этого вначале определяются их стан­дартные ошибки: S_a, S_b, S_r.

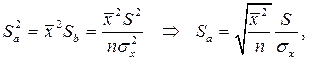
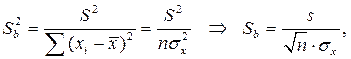
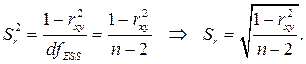
Имея в распоряжении величины a, b, r_xy и их стандартные ошибки, можно вычислить t – статистики Стьюдента для оценки значимости этих параметров.

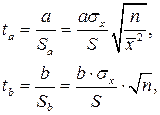
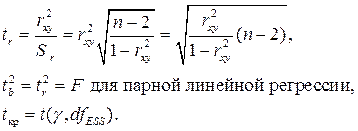
На практике для приближенной оценки руководствуются следующим правилом:

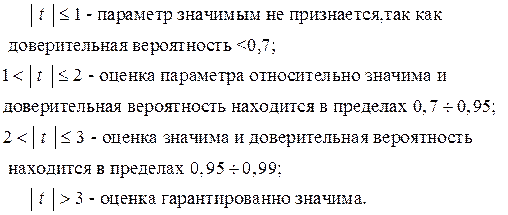
Эти правила хорошо работают при числе наблюдений больше десяти.

Важный момент: если модуль | r_xy | близок к единице и n невелико, то распределение r_xy будет отличаться от нормального и от распределения Стьюдента. Чтобы обойти это затруднение используют специальную статистику:

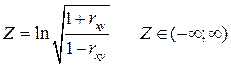
Распределение величины Z приближается к нормальному при любых допустимых значениях r; стандартная ошибка для Z – статистики и соответствующие значения t – статистик имеют вид:

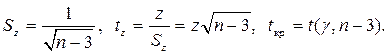
Доверительные интервалы для оценок коэффициентов модели с надёжностью 1 – γ можно вычислить следующим образом:

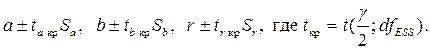
Интервалы прогноза по линейному уравнению регрессии.

Интервальная оценка для условного математического ожидания объясняемой переменной может быть записана так:

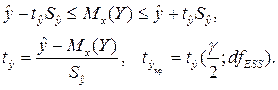
Эта статистика имеет при заданном уровне значимости γ распределение Стьюдента.

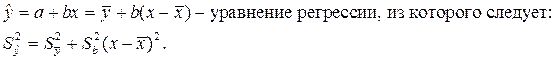
Из математической статистики известно, что 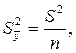а ранее вычислено:

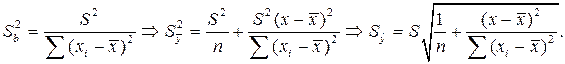
В точке прогноза x _п получим:

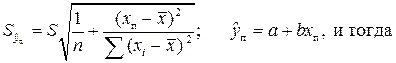
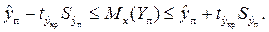
Стандартная ошибка 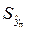характеризует ошибку положения прямой линии регрессии. Она минимальна при 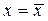и возрастает по мере удаления от этого значения.

Построенная нами доверительная область для условного математического ожидания 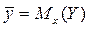определяет местоположение модельной линии регрессии, но не отдельных индивидуальных значений зависимой переменной Y.

Чтобы определить доверительный интервал для индивидуальных значений y^* зависимой переменой, следует учесть ещё один источник вариации – рассеяние вокруг самой линии регрессии, то есть 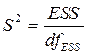. Тогда

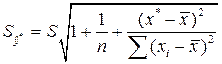и

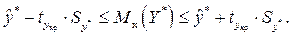
Изложенные соображения могут быть проиллюстрированы следующим рис. 3.2:

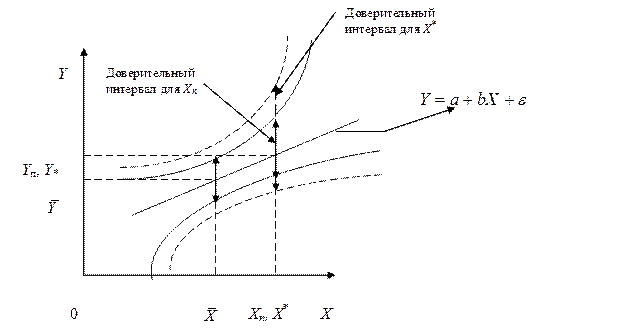рис. 3.2