Идеальный газ фермионов при низкой температуре

Рассмотрим газ невзаимодействующих фермионов в некотором объеме V. При нулевой температуре происходит «конденсация» фермионов на низшие энергетические (квантовые) уровни.[34] Благодаря запрету Паули происходит постепенное (полное) заполнение уровней до некоторого максимального уровня E ₀.[35]

d Задача. Определите максимальный уровень энергии газа фермионов при нулевой температуре.

Формула (100¢) определяет количество квантовых состояний ниже уровня E.

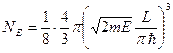. (100¢)
В соответствии с этой формулой при температуре 0 К все N фермионов расположатся ниже некоторого уровня E ₀.

.

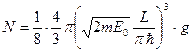Здесь g – степень дополнительного вырождения квантового энергетического уровня, связанная со спином. Для электронов g = 2.Отсюда определяем энергию E ₀ (энергию Ферми)[36].

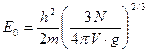. (136)

d Задача. Определите внутреннюю энергию N фермионов находящихся в объеме V при нулевой температуре.

Преобразуем формулу (116) используя (136).

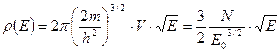
Внутренняя энергия определяется интегралом

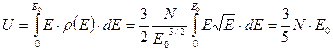. (137)

d Задача. Определите вероятность «заполнения» фермионом энергетического уровня E (распределение Ферми).

Для этого рассмотрим отдельный энергетический уровень. Большая статистическая сумма уровня

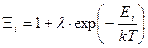. (118)
Среднее число частиц на этом уровне и определяет вероятность его заполнения (без учета спина).

.

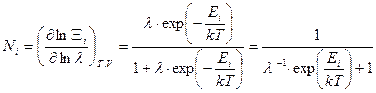Учитывая что, 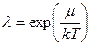записываем «распределение Ферми» в виде

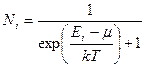. (138)
При температуре 0 К эта функция образует «ступеньку»

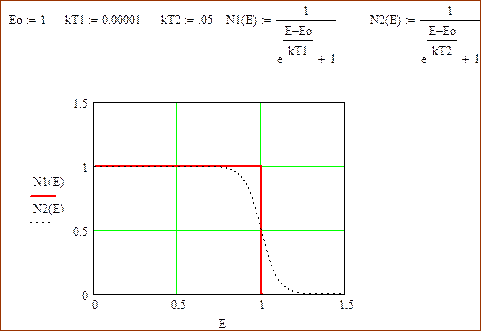
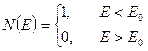. (139)
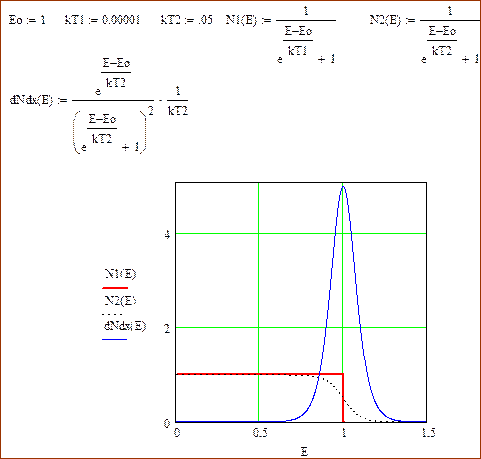
Графики функции N(E) при нулевой и «низкой» температурах.

При температурах отличных от 0 К, «ступенька» функции Ферми сглаживается. Верхний энергетический слой фермионов возбуждается, при этом энергия возбуждения порядка kT.

Определим энергию фермионов при конечной низкой температуре. Для этого записываем два интеграла.

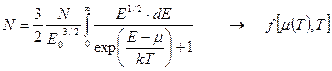. (140)
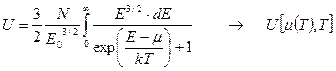. (141)
Первый интеграл является условием нормировки на число частиц, и после интегрирования дает уравнение, определяющее зависимость химического потенциала от температуры. Эту зависимость можно использовать во втором интеграле для определения энергии как функции температуры.

Ниже построен график подынтегральной функции второго интеграла. Это произведение функций: функции энергетической плотности числа состояний и функции Ферми (вероятности пребывания на энергетическом уровне). Произведение дает функцию плотности занятых уровней.

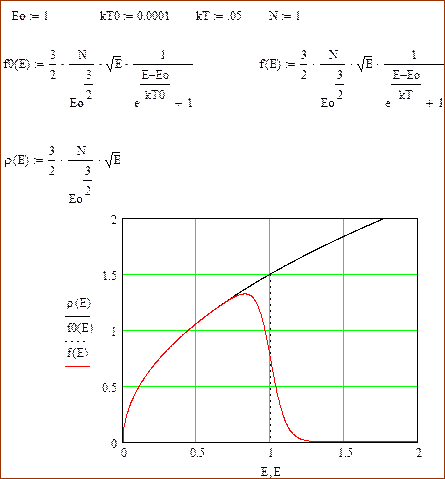
Выражения (140) и (141) содержат подобные интегралы вида

.

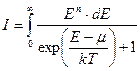Преобразуем этот интеграл, перейдя к новой переменной

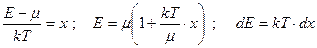. (142)
.

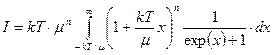Далее используем вычислительный прием, предложенный в свое время Зоммерфельдом.[37] Интегрируем по частям. Это преобразует функцию Ферми к ее производной, которая ведет себя подобно функции Дирака с «пиком» в точке перегиба функции Ферми.

Интегрируем по частям

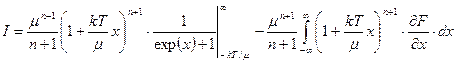. (143)
Проинтегрированная часть равна нулю. На нижнем пределе из-за нуля «скобки», на верхнем пределе равна нулю функция Ферми. В оставшейся части интеграла нижний предел интегрирования сделан бесконечным[38], так как производная функции Ферми отлична от нуля только в узкой области вблизи точки перегиба. Далее раскладываем в ряд степенную часть подынтегральной функции (ограничиваемся вторым порядком).

.

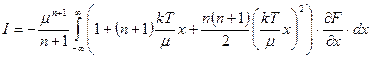Для первого интеграла следует учесть что,

.
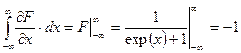Второй интеграл будет равен нулю в силу нечетности линейной функции, в то время как производная функции Ферми четная функция.

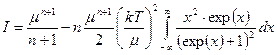. (144)
Вычислим оставшийся интеграл отдельно.

.

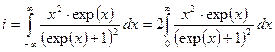Представим его в виде производной.

.

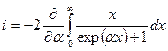Далее используем представление подынтегральной функции в виде ряда

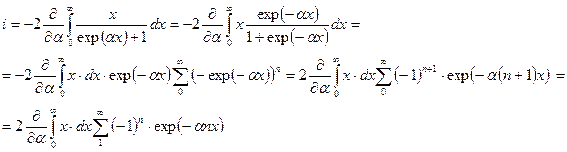. (145)
При интегрировании ряда возникают интегралы

.

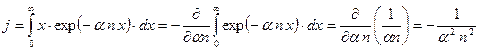Подставляем в (145).

.

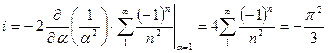Здесь образовался известный знакопеременный ряд .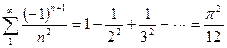

Таким образом, интеграл (144) равен

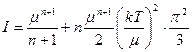. (146)
Значение интеграла подставляем в (140) и (141).

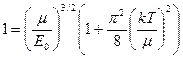. (147)
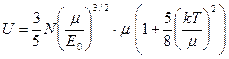. (148)
Из первого уравнения методом последовательных приближений определяем химический потенциал. Пренебрегая малым параметром (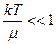), получаем в первом приближении

.

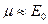Теперь это значение подставляем в «слабое» слагаемое в (147) и получаем зависимость химического потенциала от температуры во втором приближении

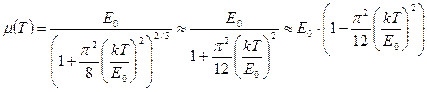. (149)
Полученную зависимость подставляем в (148), при этом в «слабое» слагаемое можно подставить m в первом приближении.

.

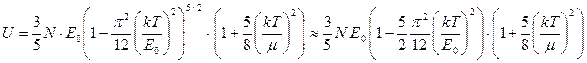Перемножая скобки и оставляя только слагаемые второго порядка, получаем энергию как функцию температуры[39]

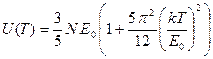. (150)
Дифференцируя (150) по температуре, получаем функцию теплоемкости идеального газа фермионов при низких температурах.

.

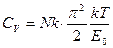Мольная теплоемкость

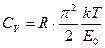. (151)
Теплоемкость при низких температурах является линейной функцией температуры.

d Задача. Оцените мольную теплоемкость электронного «газа» в металлах при комнатной температуре.

Первоначально оценим температуру вырождения электронного газа, используя высокотемпературное уравнение состояние

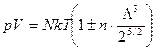. (127)
Записываем условие вырождения (квантовая поправка становится существенной)

.

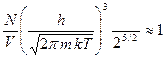Отсюда (для металлов можно считать 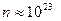эл/см³.)

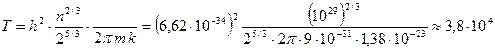К.

Таким образом, электронный газ при комнатной температуре, безусловно, вырожден и его следует считать квантовым газом.

Используя (136) и (151) вычислим энергию Ферми электронного газа.

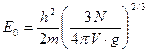. (136)
.

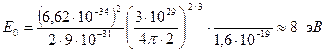Это значение подставляем в (151).

.

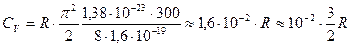Электронная теплоемкость в металлах при комнатной температуре составляет примерно один процент от классической теплоемкости электронного газа.