ЛИТЕРАТУРА: [6] п. 25.3 – 25.5
1). Интегралы вида
 где
где 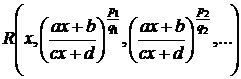 - рациональная функция своих аргументов;
- рациональная функция своих аргументов; 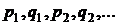 - целые числа, вычисляются с помощью подстановки
- целые числа, вычисляются с помощью подстановки  где s – наименьший общий знаменатель дробей
где s – наименьший общий знаменатель дробей 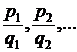
В частности, для вычисления 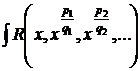 применяется подстановка
применяется подстановка  где s – наименьший общий знаменатель дробей
где s – наименьший общий знаменатель дробей 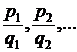
Пример 1. Найти 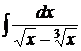 .
.
Решение. Делаем подстановку 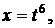 тогда
тогда
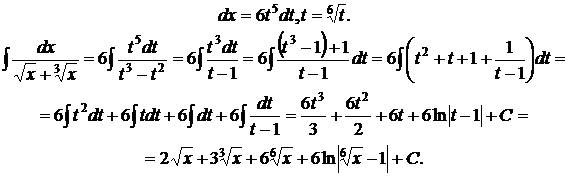
Пример 2. Найти интеграл 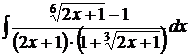
Решение.
Делаем подстановку  тогда
тогда 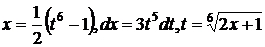 .
.

Методом неопределенных коэффициентов получаем


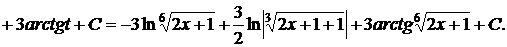
2). Интеграл от дифференциального бинома 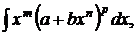 где m, n, p - рациональные числа, может быть приведен к интегралу от рациональных функций лишь в следующих трех случаях (теорема Чебышева):
где m, n, p - рациональные числа, может быть приведен к интегралу от рациональных функций лишь в следующих трех случаях (теорема Чебышева):
а) p – целое число. Полагаем 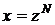 где N – общий знаменатель дробей m и n.
где N – общий знаменатель дробей m и n.
б) 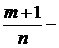 целое. Полагаем
целое. Полагаем  где N – знаменатель дроби p.
где N – знаменатель дроби p.
в) 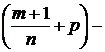 целое. Применяем подстановку
целое. Применяем подстановку 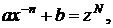 где N – знаменатель дроби p.
где N – знаменатель дроби p.
Если n = 1, то эти случаи эквивалентны следующим:
1) p – целое;
2) m – целое;
3) (m + p) – целое.
Пример 3. Найти интеграл 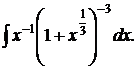
Решение. В нашем случае 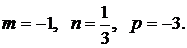 Так как p – целое (случай а), то полагаем
Так как p – целое (случай а), то полагаем 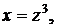 тогда
тогда 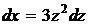 и интеграл примет вид:
и интеграл примет вид:
|
|
|

Для дальнейшего нахождения интеграла используем метод неопределенных коэффициентов
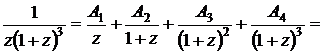
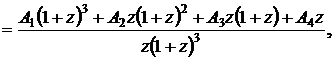 т.е.
т.е.
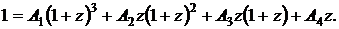
Пусть
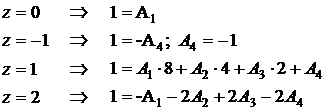

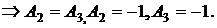
Тогда

Подставляя 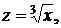 получим окончательный ответ:
получим окончательный ответ:
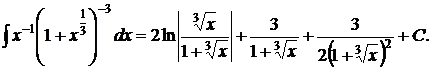
3). Для интегралов вида 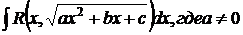

можно использовать подстановки Эйлера:
1). Если a > 0, то 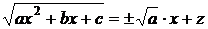
2). Если с > 0, то 
3).Если 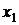 и
и 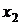 - действительные корни трехчлена
- действительные корни трехчлена 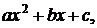 то
то 
Пример 4. Найти интеграл 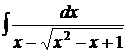
Решение. В нашем случае а = 1 > 0, используем подстановку:
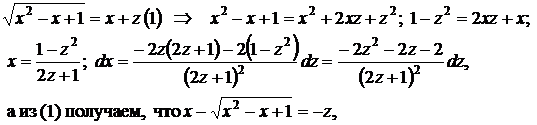
тогда интеграл
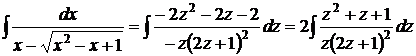
Для дальнейшего решения используем метод неопределенных коэффициентов.
Задачи:
Найти интегралы:
1). 
| 2). 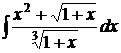
|
3). 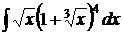
| 4). 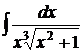
|
5). 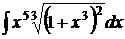
| 6). 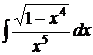
|
7). 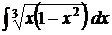
| 8). 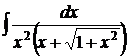
|
9). 
| 10). 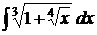
|
 2018-02-13
2018-02-13 360
360








