Теорема додавання прискорень (теорема Коріоліса)

Щоб знайти абсолютне прискорення точки , тобто її прискорення по відношенню до нерухомої системи координат, візьмемо похідну по часу від абсолютної швидкості (4.8):

          ,      (4.19)

де  – абсолютне прискорення точки .

Використовуючи міркування, які приведені вище, встановлюємо, що перший доданок, виділений круглими дужками, є переносним прискоренням, а другий доданок – відносним прискоренням точки:

                         ,                      (4.20)

                               .                           (4.21)

Третій доданок одночасно враховує рух точки  відносно рухомої системи координат і обертання рухомої системи координат відносно полюса . Цей вираз називається коріолісовим прискоренням:

                           .                       (4.22)

Вираз для коріолісового прискорення буде виведено в подальшому.

Використовуючи позначення, які прийняті у виразах (4.20) – (4.22), і підставляючи їх в (4.19), отримаємо

                                      .                                  (4.23)

Вираз (4.23) є математичним записом теореми додавання прискорень (теореми Коріоліса): при складному русі точки її абсолютне прискорення дорівнює геометричній сумі відносного, переносного і коріолісового прискорень.

Повернемось до виразу (4.20) для переносного прискорення . Прискорення центра  рухомої системи координат . На основі виразу (4.12), маємо . Тоді

                              ,                                        

                              ,                           (4.24)

                               ,                                        

де  – кутове прискорення рухомої системи координат (тіла ) при обертанні її навколо центра . Підставивши (4.24) в (4.20), маємо

                             .                         (4.25)

Другий доданок – дотичне прискорення  точки , а третій доданок – нормальне прискорення  при переносному обертальному русі тіла :

                                          ,                                      (4.26)

                                     .                                  (4.27)

Тоді остаточно для переносного прискорення  в загальному випадку руху рухомої системи координат (тіла ) можна записати:

                                      .                                  (4.28)

Розглянемо окремі випадки руху рухомої системи координат (тіла ):

1. У випадку поступального руху тіла  (), як видно з формул (4.26) – (4.27), , а переносне прискорення .

2. Якщо початок  рухомої системи координат не рухається, а система координат (тіла ) обертається навколо точки , то  і .

Виведемо простішу формулу коріолісового прискорення. Підставимо вираз (4.12) у (4.22), маємо . Остаточно отримуємо

                                       .                                   (4.29)

Коріолісове прискорення дорівнює подвоєному векторному добутку кутової швидкості переносного руху на відносну лінійну швидкість точки.

Числове значення коріолісового прискорення знаходиться як модуль векторного добутку (4.29):

                                  .                              (4.30)

Напрям коріолісового прискорення знаходиться або за правилом векторного добутку (4.29), або за правилом Жуковського (рис. 4.4).

Правило Жуковського знаходження напряму прискорення Коріоліса:

1. Провести площину, перпендикулярну вектору кутової швидкості . 2. Спроектувати відносну швидкість 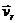 на цю площину. 3. Повернути проекцію швидкості на кут  в сторону обертання тіла . Це буде напрям коріолісового прискорення.

Коріолісове прискорення відсутнє, тобто дорівнює нулю, якщо

1. рухома система координат здійснює поступальний рух ();

2. точка  відносно тіла  не переміщується ();

3. тіло  обертається (), точка  переміщується по тілу  (), але кут між векторами відносної швидкості 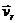 та переносної кутової швидкості обертання  тіла  складає або , або  (рис. 4.5), тобто .