Второй (предельный) признак сравнения

1 2 3 4 5 6 7

I признак сравнения

Исследовать сходимость ряда с неотрицательными членами ,

Где и , … – функции с известными наименьшими и наибольшими значениями, причем функция монотонно зависит от , …

1. Проверяем, что 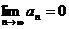. (Если , то ряд расходится, т.к. не выполнено необходимое условие сходимости ряда).

2. Поскольку , то можно применить первую теорему сравнения:

Пусть даны два ряда с неотрицательными членами и .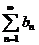

Если , то из сходимости ряда 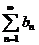следует сходимость ряда .

Если , то из расходимости ряда 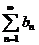следует расходимость ряда .

3. Чтобы сделать вывод о сходимости (расходимости) данного ряда, необходимо установить справедливость одной из двух гипотез:

1) Исходный ряд сходится.

2) Исходный ряд расходится.

3.1. Проверяем первую гипотезу. Чтобы установить, что исходный ряд сходится, нужно найти сходящийся ряд 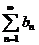такой, что .

В качестве эталонного ряда используем одни из следующих рядов:

а) сходящийся гармонический ряд при ( – константа);

б) сходящийся геометрический ряд при ( – константа).

Если существует сходящийся ряд 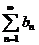такой, что выполняется неравенство , то по первой теореме сравнения исходный ряд сходится. В противном случае проверяем вторую гипотезу.

3.2. Проверяем вторую гипотезу. Чтобы установить, что исходный ряд расходится, нужно найти расходящийся ряд 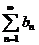такой, что .

В качестве эталонного ряда 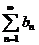используем одни из следующих рядов:

а) расходящийся гармонический ряд при ( – константа);

б) расходящийся геометрический ряд при ( – константа).

Если существует расходящийся ряд 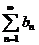такой, что выполняется неравенство , то по первой теореме сравнения исходный ряд расходится.

Замечание. Для оценки общего члена ряда используем неравенства: , ,

, , .

Примеры решения задач:

1. Исследовать на сходимость ряд .

Сравним данный ряд с рядом . Т.к. для любых значений выполняется неравенство , то из сходимости ряда будет следовать сходимость исследуемого ряда. Ряд сходится согласно интегральному признаку Коши: .

Значит, сходится и исследуемый ряд.

2. Исследовать на сходимость ряд .

Сравним данный ряд с рядом 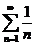. Т.к. при любых значениях выполняется неравенство

то из расходимости ряда 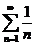будет следовать расходимость исследуемого ряда. Ряд 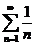расходится согласно интегральному признаку Коши:

Значит, расходится и исследуемый ряд.

Второй (предельный) признак сравнения

Исследовать сходимость ряда с положительными членами .

1. Проверяем, что 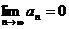, т.к. если , то ряд расходится.

2. Проверяем, что для всех .

3. Делаем вывод о сходимости или расходимости ряда, используя вторую (предельную) теорему сравнения:

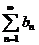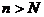
Пусть даны два ряда и , причем существует номер такой, что при всех и . Если существует конечный и отличный от нуля предел ,

то ряды и 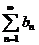либо оба сходятся, либо оба расходятся одновременно.

В качестве эталонного ряда 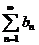обычно используют либо обобщенный гармонический ряд , который сходится при и расходится при , либо геометрический ряд , который сходится при и расходится при .

Примеры решения задач:

Исследовать на сходимость ряд .

Сравним данный ряд с рядом . По предельному признаку сравнения: .

Ряд сходится согласно интегральному признаку Коши:

Значит, сходится и исследуемый ряд.

Признак Даламбера

Исследовать сходимость ряда с положительными членами ,

Где 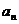содержит произведения многих сомножителей (например, степени и факториалы).

Признак Даламбера. Пусть дан ряд с положительными членами . Если существует предел

, то при ряд сходится, а при расходится. Если , то признак Даламбера ответа не дает и требуется дополнительное исследование ряда.

1. Проверяем, что 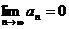, т.к. если , то ряд расходится (не выполнено необходимое условие сходимости ряда).

2. Проверяем, что для всех .

3. Вычисляем предел

4. Применяем признак Даламбера и делаем вывод о сходимости или расходимости исследуемого ряда.

Замечание. Если общий член исследуемого ряда имеет сложный вид, то в таком случае следует воспользоваться предельным признаком сравнения и применить признак Даламбера к упрощенному ряду.

Примеры решения задач:

Исследовать на сходимость ряд .