Интегральный признак Коши

Исследовать сходимость ряда с положительными членами , где , причем первообразная функции легко вычисляется.

Если , причем первообразная функции легко вычисляется, то применяем интегральный признак Коши:

Если функция , принимающая в точках значения , убывает в некотором промежутке , то ряд и несобственный интеграл либо оба сходятся, либо оба расходятся.

1. Проверяем, что 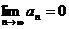, т.к. если , то ряд расходится (не выполнено необходимое условие сходимости ряда).

2. Упрощаем, если требуется, выражение для 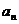, т.е. будем исследовать сходимость ряда 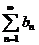, такого, что при и выбраны так, чтобы функция имела очевидную первообразную . Затем используем вторую теорему сравнения.

3. Исследуем сходимость несобственного интеграла по определению

4. Применяем интегральный признак Коши к ряду .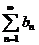

и затем делаем вывод о сходимости или расходимости исходного ряда , используя вторую (предельную) теорему сравнения.

Замечание. Интегральный признак Коши применяется в частности к рядам вида .

Примеры решения задач:

Исследовать на сходимость ряд .

Сравним данный ряд с рядом c помощью предельного признака сравнения:

Для исследования на сходимость ряда , воспользуемся интегральным признаком Коши:

Ряд сходится, значит, сходится и исследуемый ряд.

Признак Раабе

Пусть дан ряд с положительными членами .

Если существует предел , то при ряд сходится, а при расходится. Если , то признак Раабе ответа не дает и требуется дополнительное исследование ряда.

Признак Гаусса

Пусть дан ряд с положительными членами . Допустим, что для него отношение может быть представлено в виде , где или - постоянные, а - ограниченная величина, то тогда

1) ряд сходится, если или если ,

2) ряд расходится, если или , .

Примеры решения задач:

1. Исследовать ряд на сходимость по признаку Раабе.

Решение: запишем отношение .

Составим выражение Раабе: . Имеем неопределённость вида , которую раскроем по правилу Лопиталя.

Если , или , ряд сходится; если - ряд расходится.

2. Исследовать ряд на сходимость по признаку Гаусса.

Решение: , (здесь мы воспользовались формулой бинома Ньютона).

, . По признаку Гаусса ряд сходится, если , или , или .

Если - ряд расходится.

Знакопеременные ряды

Самый простой вид знакопеременных рядов – знакочередующиеся ряды.

Знакочередующийся ряд – это ряд, знаки членов которого чередуются: .

Алгоритм исследования знакочередующегося ряда на сходимость:

Составить ряд из абсолютных членов. Если он сходится, то исследуемый знакочередующийся ряд сходится абсолютно.
Если ряд, составленный из абсолютных членов, расходится, то следует использовать признак Лейбница: а) , б) .