В теории вероятностей и ее приложениях важную роль играет так называемый принцип двойственности, который может быть выражен соотношениями:
 , (6.1)
, (6.1)
 . (6.2)
. (6.2)
Из равенства (6.1) следует (6.2) и наоборот. Например, выполним замену в (6.1)  ,
,  , тогда (6.1)
, тогда (6.1)  или
или  , что совпадает с (6.2).
, что совпадает с (6.2).
Возьмем в (6.1) дополнение в обеих частях и поменяем местами правую и левую части, тогда
 , (6.3)
, (6.3)
теперь из (6.1) можно получить (6.3), если события  и
и  заменить на противоположные
заменить на противоположные  и
и  , объединение на пересечение и наоборот – пересечение на объединение. Таким образом, для всякого утверждения, относящегося к некоторой системе событий, может быть сформулировано эквивалентное ему двойственное утверждение путем указанной замены событий и операций над событиями.
, объединение на пересечение и наоборот – пересечение на объединение. Таким образом, для всякого утверждения, относящегося к некоторой системе событий, может быть сформулировано эквивалентное ему двойственное утверждение путем указанной замены событий и операций над событиями.
К принципу двойственности следует отнести еще одно соотношение:
 , (6.4)
, (6.4)
геометрическая интерпретация которого очевидна и представлена на рис. 6.1, где  отмечено горизонтальной штриховкой и
отмечено горизонтальной штриховкой и  – вертикальной штриховкой.
– вертикальной штриховкой.
|
|
|

Рис. 6.1. События  ,
,  и их дополнения.
и их дополнения.
Рассмотрим геометрическое доказательство соотношения (6.1). Его левую часть можно представить областью с горизонтальной штриховкой, рис.6.2. Аналогично на рис. 6.3 выделены события:  – горизонтальной
– горизонтальной

Рис. 6.2. Дополнение объединения двух событий  и
и  .
.
штриховкой,  – вертикальной штриховкой и
– вертикальной штриховкой и  – штриховкой "в клеточку".
– штриховкой "в клеточку".

Рис. 6.3. Пересечение дополнений двух событий  и
и  .
.
Таким образом, левая и правая части соотношения (6.1) совпадают.
Условные вероятности
Пусть события 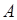 и
и 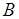 имеют вероятности
имеют вероятности  и
и  . Рассмотрим вероятность события
. Рассмотрим вероятность события 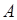 , если известно, что произошло событие
, если известно, что произошло событие 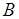 . При этом в общем случае вероятность события
. При этом в общем случае вероятность события 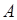 изменяется и становится отличной от
изменяется и становится отличной от  . Эта вероятность обозначается
. Эта вероятность обозначается  и называется условной вероятностью события
и называется условной вероятностью события 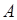 при условии, что
при условии, что 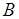 произошло, или просто – вероятностью
произошло, или просто – вероятностью  при условии
при условии  .
.
Следует различать две ситуации. 1). Если  , то события
, то события 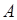 и
и 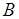 зависимые. 2). Если
зависимые. 2). Если  , то события
, то события 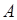 и
и 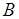 независимые. Рассмотрим пример: бросание игральной кости. Пусть событие
независимые. Рассмотрим пример: бросание игральной кости. Пусть событие 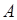 - это выпадение единицы,
- это выпадение единицы, 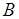 - выпадение нечетного числа. Тогда
- выпадение нечетного числа. Тогда  =1/6, а
=1/6, а  =1/3, следовательно
=1/3, следовательно  и
и  - зависимые события.
- зависимые события.
Если 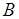 - результат опыта, то
- результат опыта, то  называют доопытной или априорной вероятностью события
называют доопытной или априорной вероятностью события 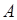 , а условную вероятность
, а условную вероятность  - послеопытной или апостериорной вероятностью события
- послеопытной или апостериорной вероятностью события 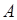 .
.
 2020-01-15
2020-01-15 484
484








