2020-01-15
113
Пусть 
- полная группа несовместных событий. Тогда выполняются условия:
(12.1)
- достоверное событие и для любых 
пересечение 
- невозможное событие. Представим некоторое событие 
в виде
. (12.2)
Далее используем свойство дистрибутивности пересечения относительно объединения, тогда
. (12.3)
Отметим, что при любых события 
и 
несовместны. Действительно, 
. Поэтому из (12.3) следует
(12.4)
или, выражая вероятность пересечения через произведение вероятностей согласно (9.5),
. (12.5)
Равенство (12.5) называется формулой полной вероятности. 
В частном случае попарно независимых событий 
и 
условные вероятности 
и преобразуется следующим образом:
.
Таким образом, для независимых событий и 
формула (12.5) вырождается в равенство 
.
Формула Байеса
Пусть также как в п.12 несовместные события образуют полную группу и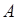 
- некоторое событие. Согласно формуле умножения вероятностей (9.5)
|
|
|
. (13.1)
Отсюда
. (13.2)
Здесь знаменатель 
можно представить по формуле полной вероятности (12.5). Тогда
. (13.3)
Формулы (13.2) и (13.3) называются формулами Байеса.
Формулам Байеса может быть дана следующая интерпретация. Пусть событие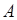 
- это исход опыта. Тогда вероятности 
можно назвать априорными или доопытными, а вероятности 
- апостериорными или послеопытными. Таким образом, формула (13.3) связывает между собой априорные и апостериорные вероятности событий 
, т.е. позволяют учесть информацию, полученную в результате опыта и ее влияние на вероятность событий 
.
Для независимых событий 
и условные вероятности 
, тогда правая часть (13.3) преобразуется следующим образом:
,
и формула (13.3) принимает вид 
.
