Алгебраическое решение

.

Пусть . Выясним, при каких значениях  выполняется неравенство , то есть решим неравенство

.

Пусть , тогда рассмотрим неравенство

.

Ответ: Если  или 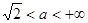, то данное уравнение корней не имеет.

    Если , то уравнение имеет единственный корень .

Если , то уравнение имеет два корня .

В данном случае оба решения равноценны, можно решать любым способом. Зато уже в следующем примере решение с помощью тригонометрической подстановки проще.

Пример 2. При каких а неравенство

имеет решение [13].

Неравенство  имеет решение при а большем наименьшего значения выражения .

Решение с помощью тригонометрической подстановки

Положим , тогда

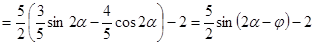, где .

Оценим выражение

.

Наименьшее значение выражения  равно . Значит, при  неравенство имеет решение.

Ответ: при  неравенство имеет решение.

Алгебраическое решение

Если , то неравенство примет вид

.

Значит, при  неравенство имеет решение.

Поделим числитель и знаменатель на , получим

.

Введем замену , тогда

.

Найдем наименьшее значение выражения .

.

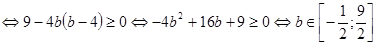То есть наименьшее значение выражения  равно . Тогда наименьшее значение выражения , а значит наименьшее значение выражения  равно .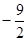

Ответ: при  неравенство имеет решение.

Для данного задания самый удобный метод решения – решение с помощью тригонометрической подстановки. Во втором случае возникает проблема с тем, чтобы найти наименьшее значение выражения . Если учащиеся умеют находить наименьшее значение функции с помощью производной, то выполнив все вычисления и проведя исследование, они справятся с задачей. Если подобное задание решать до изучения производной, то могут возникнуть трудности с определением наименьшего значения. В работе предложен прием сведения к уравнению с параметром, подробно описанный в предыдущем параграфе.

Глава 3

Опытное преподавание темы «Применение тригонометрической подстановки для решения алгебраических задач»