2020-01-14
250
В регрессионном анализе рассматривается односторонняя зависимость случайной зависимой переменной Y от одной (или нескольких) неслучайной независимой переменной Х, называемой часто объясняющей переменной. Такая зависимость может возникнуть, например, в случае, когда при каждом фиксированном значении X соответствующие значения Y подвержены случайному разбросу за счет действия неконтролируемых факторов. Указанная зависимость Y от X (иногда ее называют регрессионной) может быть представлена также в виде модельного уравнения регрессии (1.1). В силу воздействия неучтенных случайных факторов и причин отдельные наблюдения y будут в большей или меньшей мере отклоняться от функции регрессии 
. В этом случае уравнение взаимосвязи двух переменных (парная регрессионная модель) может быть представлено в виде: 
, где 
— случайная переменная, характеризующая отклонение от функции регрессии. Эту переменную будем называть возмущающей или просто возмущением. Таким образом, в регрессионной модели зависимая переменная Y есть некоторая функция 
(Х) с точностью до случайного возмущения .
Рассмотрим линейный регрессионный анализ, для которого функция (Х) линейная относительно оцениваемых параметров:
. (2.1)
Предположим, что для оценки параметров линейной функции регрессии (2.1) взята выборка, содержащая n пар значений переменных (
), где i=1,2,..., 
. В этом случае линейная парная регрессионная модель имеет вид:
(2.2)
Отметим основные предпосылки регрессионного анализа:
1. В модели (2.2) возмущение 
(или зависимая переменная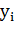 
) есть величина случайная, а объясняющая переменная 
— величина неслучайная.
2. Математическое ожидание возмущения равно нулю: 
(или математическое ожидание зависимой переменной 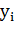равно линейной функции регрессии:
M()=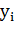 
(2.3)
3. Дисперсия возмущения (или зависимой переменной 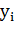) постоянна для любого i:
(2.4)
(или D() =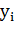 
— условие гомоскедастичности или равноизменчивости возмущения (зависимой переменной)).
4. Возмущения (или переменные и) не коррелированы.
(i 
(2.5)
5. Возмущение , (или зависимая переменная 
) есть нормально распределенная случайная величина.
Для получения уравнения регрессии достаточно первых четырех предпосылок. Требование выполнения пятой предпосылки (т.е. рассмотрение «нормальной регрессии») необходимо для оценки точности уравнения регрессии и его параметров.
Оценкой модели (2.2) по выборке является уравнение регрессии:
(1.8). Параметры этого уравнения 
и 
определяются на основе метода наименьших квадратов.
Теорема Гауса-Маркова. Если регрессионная модель удовлетворяет предпосылкам 1-4, то оценки и имеют наименьшую дисперсию в классе линейных несмещенных оценок, т.е. являются эффективными оценками параметров и .
Воздействие неучтенных случайных факторов и ошибок наблюдений в модели (2.2) определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии . Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия
(2.6)
где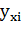 
— групповая средняя, найденная по уравнению регрессии;
— выборочная оценка возмущения , или остаток регрессии.
В знаменателе выражения (2.6) стоит число степеней свободы n—2, а не n, так как две степени свободы теряются при определении двух параметров прямой и .
