Виконавець Керівник роботи
Студентка групи ЗММ-00-01к. ф. - м. н., доцент
Лісняк Л.В. Трактинська В.М.
“___” червня 200_ р. “____" червня 200_ р.
Допускається до захисту
Завідувач кафедроюРецензент
доктор фіз. - мат. наук, професорк. ф. - м. н., доцент
Бабенко В.Ф. Великін В.Л.
“___” червня 200_ р. “___”червня 200_ р.
м. Дніпропетровськ 200_ р.
Реферат
Дипломна робота містить 105 стор., 95 рис., 5 табл.., 7 джерел.
Об’єктом дослідження є задачі з параметрами.
Мета роботи - систематизувати графічні методи розв’язання задач з параметрами.
Методика дослідження - вивчення метода та розв’язування задач.
Результати досліджень можуть бути застосовані при викладанні теми “Графічні методи розв’язування задач із параметрами" в математичних класах середніх шкіл та ліцеях.
Перелік ключових слів: ПАРАМЕТР, ФУНКЦІЯ, РОЗВ’ЯЗОК, РІВНЯННЯ, НЕРІВНІСТЬ, ПАРАЛЕЛЬНИЙ ПЕРЕНОС, ПОВОРОТ, ГОМОТЕТІЯ, КООРДИНАТНА ПЛОЩИНА, ПОХІДНА.
Annotation
This degree thesis of the 5th year student (DNU, Faculty of Mechanics and Mathematics, Department of Mathematical Analysis) deals with graphic methods of the decision of problems with parameters. The work is interesting for the students and post-graduates students of mathematical specialties.
|
|
|
Bibliography: 7
Зміст
Вступ
Розділ 1. Координатна площина 
1.1 Паралельний перенос
1.2 Поворот
1.3 Гомотетія. Стиск до прямої
1.4 Дві прямі на площині
Розділ 2. Координатна площина (x; a)
Розділ 3. Застосування похідної
Список використаної літератури
Вступ
В програмах по математиці для середніх шкіл задачам з параметрами відводять незначне місце. Тому, в перше чергу, необхідно вказати розділи загальноосвітньої математики, в яких присутня сама ідея параметра.
Так, з параметрами учні зустрічаються при введенні деяких понять. Розглянемо як приклади наступні об’єкти:
функція пряма пропорційність  (де
(де  - змінні,
- змінні,  - параметр,
- параметр,  );
);
лінійна функція  (де
(де  - змінні,
- змінні,  - параметри);
- параметри);
лінійне рівняння  (де
(де 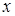 - змінна,
- змінна,  - параметри);
- параметри);
рівняння першої степені  (де
(де 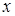 - змінна,
- змінна,  - параметри,
- параметри,  );
);
квадратне рівняння  (де
(де 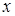 - змінна,
- змінна,  - параметри,
- параметри,  );
);
До задач з параметрами, які розглядаються в курсі середньої школи, можна
віднести, наприклад, пошук розв’язків лінійних та квадратних рівнянь в загальному виді, дослідження кількості їх коренів в залежності від значень параметрів
Природно, що такий невеликий клас задач багатьом учням не дозволяє усвідомити головне: параметр (фіксоване, але невідоме число) має двоїсту природу. По-перше, параметр можна розглядати як число, а по-друге, - це невідоме число. Таким чином, ділення на вираз, який містить параметр, добування кореня парного ступеня із таких виразів потребує попередніх досліджень. Як правило, результати досліджень впливають і на розв’язок, і на відповідь.
|
|
|
Головне, що необхідно усвідомити при роботі з параметром - це необхідність обережного відношення до фіксованого, але невідомого числа.
Дипломна робота присвячена розробці методики викладання теми “Графічні методи розв’язування задач з параметрами”.
Робота складається із вступу, 3 розділів та списку використаної літератури. Кожний із 3 розділів присвячений одному із графічних прийомів. Розділи діляться на параграфи. Кожний параграф побудовано за такою структурою. На початку параграфа наводиться необхідний теоретичний матеріал, потім даються задачі із подробним розв’язанням, а наприкінці наведені задачі для самостійної роботи з відповідями.
І розділ роботи “Координатна площина  " присвячений побудові графічного образу на координатній площині
" присвячений побудові графічного образу на координатній площині  .
.
ІІ розділ роботи “Координатна площина  " присвячений побудові графічного образу на координатній площині
" присвячений побудові графічного образу на координатній площині  .
.
ІІІ розділ роботи “Застосування похідної” присвячений побудові графічного образу із застосуванням похідної.
Дипломна робота може бути використана вчителями та студентами старших курсів при проведенні педагогічної практики.
Розділ 1. Координатна площина 
На площині  функція
функція  задає сім’ю кривих, які залежать від параметра
задає сім’ю кривих, які залежать від параметра  . Кожній сім’ї функцій
. Кожній сім’ї функцій  властиві деякі властивості. Нас буде цікавити питання: за допомогою якого перетворення площини (паралельний перенос, поворот, гомотетія і т.д.) можна перейти від однієї кривої сім’ї до будь-якої іншої. Кожному з таких перетворень буде присвячено окремий підрозділ.
властиві деякі властивості. Нас буде цікавити питання: за допомогою якого перетворення площини (паралельний перенос, поворот, гомотетія і т.д.) можна перейти від однієї кривої сім’ї до будь-якої іншої. Кожному з таких перетворень буде присвячено окремий підрозділ.
Не завжди графічний образ сім’ї функцій  описується простим перетворенням. Тому в таких ситуаціях необхідно зосередити увагу не на тому, як пов’язані криві однієї сім’ї, а на самі криві. Іншими словами, можна виділити ще один тип задач, в яких ідея розв’язку перш за все заснована на властивостях конкретних геометричних фігур, а не властивостях сім’ї взагалі. Нас будуть цікавити прямі та параболи. Такий вибір обумовлено окремим (основним) положенням лінійної та квадратичної функції в шкільній математиці.
описується простим перетворенням. Тому в таких ситуаціях необхідно зосередити увагу не на тому, як пов’язані криві однієї сім’ї, а на самі криві. Іншими словами, можна виділити ще один тип задач, в яких ідея розв’язку перш за все заснована на властивостях конкретних геометричних фігур, а не властивостях сім’ї взагалі. Нас будуть цікавити прямі та параболи. Такий вибір обумовлено окремим (основним) положенням лінійної та квадратичної функції в шкільній математиці.
Говорячи про графічні методи, неможливо обійти одну проблему, породжену практикою конкурсних екзаменів. Мається на увазі питання про законність розв’язку, який заснований на графічних зображеннях. З формальної точки зору результат, який “знятий" з рисунку, знайдений нестрого. Але вимоги до рівня математичної строгості для учня повинні визначатися здоровим глуздом.
Побудова графічних образів в даній роботі заснована на побудові графіків виду  за допомогою перетворень графіка функції
за допомогою перетворень графіка функції  .
.
Паралельний перенос
Почнемо з задач, в який членами сім’ї кривих  будуть прямі.
будуть прямі.
1. Для кожного значення параметра а визначити число розв’язків рівняння  .
.
Розв’язання. Побудуємо графіки функцій  та
та  .
.
З рисунка 1.1.1 випливає, що при  - розв’язків немає, при
- розв’язків немає, при  - 2 розв’язки, при
- 2 розв’язки, при  - 4 розв’язки, при
- 4 розв’язки, при  - 3 розв’язки, при
- 3 розв’язки, при  - 2 розв’язки.
- 2 розв’язки.

Рис.1.1.1
Відповідь: при  - розв’язків немає, при
- розв’язків немає, при  - 2 розв’язки, при
- 2 розв’язки, при  - 4 розв’язки, при
- 4 розв’язки, при  - 3 розв’язки, при
- 3 розв’язки, при  - 2 розв’язки.
- 2 розв’язки.
2. Для кожного значення параметра  визначити число розв’язків рівняння
визначити число розв’язків рівняння  .
.
Розв’язання. Побудуємо графік функції  . Знайдемо ОДЗ функції
. Знайдемо ОДЗ функції  , тобто
, тобто  .
.
З рисунка 1.1.2 випливає, що при  - розв’язків немає, при
- розв’язків немає, при  - 3 розв’язки, при
- 3 розв’язки, при  - 4 розв’язки, при
- 4 розв’язки, при  - 2 розв’язки, при
- 2 розв’язки, при  - немає розв’язків.
- немає розв’язків.

Рис.1.1.2
Відповідь: при  - розв’язків немає, при
- розв’язків немає, при  - 3 розв’язки, при
- 3 розв’язки, при  - 4 розв’язки, при
- 4 розв’язки, при  - 2 розв’язки, при
- 2 розв’язки, при  - немає розв’язків.
- немає розв’язків.
3. Знайти число розв’язків рівняння  .
.
Розв’язання. Побудуємо графік функції  .
.

Рис.1.1.3
З рисунка 1.1.3 випливає, що при  - розв’язків немає, при
- розв’язків немає, при  - розв’язки
- розв’язки  або
або  , при
, при  - 4 розв’язки, при
- 4 розв’язки, при  - 3 розв’язки, при
- 3 розв’язки, при  - 2 розв’язки.
- 2 розв’язки.
|
|
|
Відповідь: при  - розв’язків немає, при
- розв’язків немає, при  - розв’язки
- розв’язки  або
або  , при
, при  - 4 розв’язки, при
- 4 розв’язки, при  - 3 розв’язки, при
- 3 розв’язки, при  - 2 розв’язки.
- 2 розв’язки.
4. Розв’язати рівняння  .
.
Розв’язання. Побудуємо графік функції  . Знайдемо ОДЗ:
. Знайдемо ОДЗ:  , звідси
, звідси  .
.

Рис.1.1.4
Розв’язуючи рівняння  , знаходимо
, знаходимо  .
.
Якщо  , то
, то  ; якщо
; якщо  , то
, то  або
або  .
.
Якщо  або
або  , то
, то  , звідси якщо
, звідси якщо  , то
, то  , якщо
, якщо  , то розв’язків немає.
, то розв’язків немає.
5. При яких а рівняння  має рівно три розв’язки?
має рівно три розв’язки?
Розв’язання. Побудуємо графіки функцій  та
та  .
.

Рис.1.1.5
Графіки  та
та  мають три точки перетину при а=-1 та а=-0,5.
мають три точки перетину при а=-1 та а=-0,5.
Відповідь: а=-1 та а=-0,5.
6. При яких значення параметра а рівняння  має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання. Побудуємо сім’ю функцій  , а точніше графіки
, а точніше графіки
функцій  та
та  . Знайдемо ОДЗ рівняння:
. Знайдемо ОДЗ рівняння:  .
.

Рис.1.1.6
Графіки функцій  та
та  мають одну точку перетину при
мають одну точку перетину при  та
та  .
.
Відповідь:  та
та  .
.
7. При яких значеннях а рівняння  має два корені?
має два корені?
Розв’язання. Побудуємо графіки функцій  та
та  . ОДЗ:
. ОДЗ:  , звідки
, звідки  . Знаходимо дві точки перетину графіків:
. Знаходимо дві точки перетину графіків:  , звідси
, звідси  ,
,  . Тоді для параметра
. Тоді для параметра  справедлива нерівність
справедлива нерівність  .
.

Рис.1.1.7
Відповідь:  .
.
8. Розв’язати нерівність  .
.
Розв’язання. Побудуємо графік прямої  та пів парабол
та пів парабол  .
.

Рис.1.1.8
Якщо пів парабола розташована нижче прямої, то нерівність розв’язків немає. Розв’язки з’являються тільки з моменту дотику. Знайдемо значення параметра  , яке відповідає моменту дотику двох функцій:
, яке відповідає моменту дотику двох функцій:  , звідси
, звідси  ,
,  , звідси
, звідси  . При
. При  маємо 1 розв’язок. Тобто, при
маємо 1 розв’язок. Тобто, при  нерівність розв’язків немає.
нерівність розв’язків немає.
Якщо  , то
, то  .
.
Далі, зсуваючи півпараболу ліворуч, зафіксуємо момент, коли графіки  ,
,  мають дві спільні точки. Таке розташування забезпечує вимога:
мають дві спільні точки. Таке розташування забезпечує вимога:  , тоді розв’язком буде відрізок
, тоді розв’язком буде відрізок  .
.
Коли півпарабола і пряма перетинаються тільки в одній точці (це відповідає випадку  ), то розв’язком буде відрізок
), то розв’язком буде відрізок  .
.
9. При яких  рівняння
рівняння  має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання. Запишемо задане рівняння в такому виді:  . Права частина рівняння
. Права частина рівняння  задає нерухомий “кут", ліва частина
задає нерухомий “кут", ліва частина  - “кут", вершина якого рухається по вісі абсцис.
- “кут", вершина якого рухається по вісі абсцис.

Рис.1.1.9
Задане рівняння буде мати єдиний розв’язок, якщо одна з сторін рухомого “кута" пройде через точку (-1,3). Маємо  , звідки
, звідки  або
або  .
.
|
|
|
Відповідь:  або
або  .
.
10. Знайти всі значення параметра  , при яких система рівнянь
, при яких система рівнянь  має розв’язки.
має розв’язки.
Розв’язання. З першого рівняння системи знаходимо  .
.
Це рівняння задає сім’ю парабол, які “ковзають" вершинами вздовж прямої  . З другого рівняння знаходимо
. З другого рівняння знаходимо  - коло з центром в точці (1, 0) радіуса 1.
- коло з центром в точці (1, 0) радіуса 1.

Рис.1.1.10
З’ясуємо, при яких значення параметра сім’я парабол має спільні точки з колом.
Випадок дотику знайдемо з системи  , вимагаючи від системи мати один розв’язок. Одну спільну точку графіки мають при
, вимагаючи від системи мати один розв’язок. Одну спільну точку графіки мають при  або
або  . Якщо
. Якщо  , то система має два розв’язки.
, то система має два розв’язки.
Відповідь:  .
.
Задачі для самостійної роботи
1. Знайти всі значення параметра b, при яких рівняння  має єдиний Розв’язання.
має єдиний Розв’язання.
Розв’язання. Позначимо  . Запишемо рівняння, яке рівносильне початковому:
. Запишемо рівняння, яке рівносильне початковому:  . Переходимо до рівносильної системи
. Переходимо до рівносильної системи

Будуємо графік функції  з областю визначення
з областю визначення  та
та  (рис.1.1.11).
(рис.1.1.11).

Рис.1.1.11
Знайдений графік сім’я прямих  повинна перетинати тільки в одній точці. З рисунка видно, що ця вимога виконується лише при а > 2, тобто lg b > 2, b > 100.
повинна перетинати тільки в одній точці. З рисунка видно, що ця вимога виконується лише при а > 2, тобто lg b > 2, b > 100.
Відповідь: b > 100.
2. При яких значеннях параметра  нерівність
нерівність  має розв’язки?
має розв’язки?
Розв’язання. Графіком функції  є півколо з центром (0; 0) та радіусом 1 (рис.1.1.12). Функція
є півколо з центром (0; 0) та радіусом 1 (рис.1.1.12). Функція  для кожного фіксованого значення параметра задає пряму, тобто рівняння
для кожного фіксованого значення параметра задає пряму, тобто рівняння  на координатній площині (х; у) породжує систему паралельних прямих.
на координатній площині (х; у) породжує систему паралельних прямих.

Рис.1.1.12
Нам необхідно визначити ті значення параметра, при яких знайдуться точки півкола, розташовані вище відповідних точок прямої. Такі точки з’являться після того, як пряма  займе положення зліва від дотичної. Моменту дотику відповідає
займе положення зліва від дотичної. Моменту дотику відповідає  . Таким чином, при
. Таким чином, при  дана нерівність має розв’язки.
дана нерівність має розв’язки.
Відповідь:  .
.
3. При яких значеннях параметра а корені рівняння  мають однакові знаки?
мають однакові знаки?
Розв’язання. Перша сім’я  задає систему "кутів", сторони яких утворюють кути по 45° с віссю абсцис. Вершини знаходяться на вісі х, причому праворуч від початку координат (а = 0 нас не задовольняє, так як в цьому випадку початкове рівняння має корені різних знаків). Друга сім’я
задає систему "кутів", сторони яких утворюють кути по 45° с віссю абсцис. Вершини знаходяться на вісі х, причому праворуч від початку координат (а = 0 нас не задовольняє, так як в цьому випадку початкове рівняння має корені різних знаків). Друга сім’я  являє собою множину прямих, паралельних вісі абсцис. Ці прямі повинні перетинати "кути" в точках, абсциси яких мають однакові знаки. По рис.1.1.13 легко знайти умову для параметра, яке задовольняє вимогам задачі.
являє собою множину прямих, паралельних вісі абсцис. Ці прямі повинні перетинати "кути" в точках, абсциси яких мають однакові знаки. По рис.1.1.13 легко знайти умову для параметра, яке задовольняє вимогам задачі.

Рис.1.1.13
Маємо

Розв’язавши цю систему, знайдемо
Відповідь.  або
або  .
.
4. Знайти всі значення параметра а, при кожному з яких рівняння  має три різних кореня.
має три різних кореня.
Розв’язання. Графік функції  для
для  наведено на рис.1.1.14.
наведено на рис.1.1.14.

Рис.1.1.14
При а = 0 рівняння має єдиний корінь.
З сім’ї паралельних прямих у = х-а нас цікавлять тільки ті, які перетинають побудований графік в трьох точках. Очевидно таких прямих тільки дві. Вони й побудовані на рисунку 1.1.14. Для прямої 1 маємо  , а для прямої 11 маємо
, а для прямої 11 маємо  . Оскільки
. Оскільки  , то знаходимо
, то знаходимо
Відповідь:  або
або  .
.
Тепер будемо розглядати сім’ї кривих, які задаються рівняннями  або
або  ,
,  . Членами цих сімей будуть "півпараболи".
. Членами цих сімей будуть "півпараболи".
5. Розв’язати нерівність  .
.
Розв’язання. Побудуємо прямую  (рис.1.1.15). Якщо "пів парабола"
(рис.1.1.15). Якщо "пів парабола"  розташована нижче прямої, то очевидно нерівність розв’язків не має (рис.15, положення I). Розв’язки з’являються тільки з моменту дотику (положення II).
розташована нижче прямої, то очевидно нерівність розв’язків не має (рис.15, положення I). Розв’язки з’являються тільки з моменту дотику (положення II).

Рис.1.1.15
Значення параметра, яке відповідає дотику, можна знайти, вимагаючи від системи

мати один Розв’язання, що рівносильне для рівняння  мати один корінь. Звідси знаходимо
мати один корінь. Звідси знаходимо  . Таким чином, при
. Таким чином, при  початкова нерівність розв’язків не має.
початкова нерівність розв’язків не має.
Далі, зсуваючи "півпараболу" ліворуч, зафіксуємо останній момент, коли графіки  та
та  мають дві спільні точки (положення III). Таке розташування забезпечується вимогою
мають дві спільні точки (положення III). Таке розташування забезпечується вимогою  .
.
При  відрізок
відрізок  , де
, де  та
та  - абсциси точок перетину графіків, буде розв’язком початкової нерівності. Розв’язав наведене вище рівняння, знаходимо
- абсциси точок перетину графіків, буде розв’язком початкової нерівності. Розв’язав наведене вище рівняння, знаходимо  ,
,  . Таким чином, якщо
. Таким чином, якщо  , то
, то  .
.
Коли "півпарабола" та пряма перетинаються тільки в одній точці (це відповідає випадку  ), то розв’язком буде відрізок
), то розв’язком буде відрізок  , де
, де  - більший з коренів
- більший з коренів  та
та  ( положення IV).
( положення IV).
Відповідь: при  розв’язків не має; при
розв’язків не має; при 
 ; при
; при  , розв’язком буде відрізок
, розв’язком буде відрізок  , де
, де  - більший з коренів
- більший з коренів  та
та  .
.
6. Скільки коренів має рівняння  в залежності від значень параметра а?
в залежності від значень параметра а?
Розв’язання. Зазначимо, що вводячи функції  та
та  , ми одержуємо одразу дві сім’ї кривих. В цьому випадку пошук спільних точок провести важко. Однак задачу можна спростити, використавши заміну
, ми одержуємо одразу дві сім’ї кривих. В цьому випадку пошук спільних точок провести важко. Однак задачу можна спростити, використавши заміну  . Звідси знаходимо
. Звідси знаходимо  .
.
Розглянемо функції  (рис.1.1.16). Серед них лише одна задає сім’ю кривих.
(рис.1.1.16). Серед них лише одна задає сім’ю кривих.

Рис.1.1.16
Очевидно, якщо абсциса вершини "півпараболи" більше одиниці, тобто  , то рівняння коренів не має.
, то рівняння коренів не має.
Якщо  , то по рисунку видно, що графіки перетинаються, причому тільки в одній точці, оскільки функції
, то по рисунку видно, що графіки перетинаються, причому тільки в одній точці, оскільки функції  та
та  мають різний характер монотонності.
мають різний характер монотонності.
Відповідь. Якщо  , то рівняння має один корінь; якщо
, то рівняння має один корінь; якщо  , то рівняння коренів не має.
, то рівняння коренів не має.
7. Знайти всі значення параметра а, при яких система рівнянь має розв’язки

Розв’язання. З першого рівняння системи знайдемо  при
при  . Це рівняння задає сім’ю "півпарабол" (параболи
. Це рівняння задає сім’ю "півпарабол" (параболи  "сковзають" вершинами по вісі абсцис, причому ми розглядаємо лише праву вітку).
"сковзають" вершинами по вісі абсцис, причому ми розглядаємо лише праву вітку).
Ліву частину другого рівняння системи розкладемонамножники. Маємо

Тільки графіком другого рівняння є об’єднання двох прямих  и
и  .
.
З’ясуємо, при яких значеннях параметра а сім’я "півпарабол" має хоча б одну спільну точку з однією зі знайдених прямих.

Рис.1.1.17
Скористаємося рис.1.1.17. Якщо вершини "півпарабол" знаходяться праворуч від точки А, але ліворуч від точки В (точка В відповідає положенню вершини в момент дотику "півпараболи" з прямою  ), то очевидно графіки спільних точок не мають.
), то очевидно графіки спільних точок не мають.
Якщо вершина розташована в точці А, то очевидно а = −3. Випадок дотику знайдемо, вимагаючи від системи

мати один Розв’язання, тобто рівняння  повинно мати один корінь. Звідси знаходимо а =
повинно мати один корінь. Звідси знаходимо а =  .
.
Таким чином, початкова система не має розв’язків, якщо  и відповідно має розв’язки, якщо
и відповідно має розв’язки, якщо  та
та  . Відповідь.
. Відповідь.  або
або  .
.
8. Знайти найменше с,при якому система має єдиний розв’язок

Розв’язання. Перше рівняння системи зручно представити у вигляді  . Це рівняння задає сім’ю кіл постійного радіуса, рівного 1, причому центри кіл лежать на прямій
. Це рівняння задає сім’ю кіл постійного радіуса, рівного 1, причому центри кіл лежать на прямій  . Побудуємо графік функції
. Побудуємо графік функції  (рис.1.1.18). На цьому ж рисунку показано чотири положення кола, при яких початкова система має єдиний Розв’язання.
(рис.1.1.18). На цьому ж рисунку показано чотири положення кола, при яких початкова система має єдиний Розв’язання.
Кожному з відмічених кіл відповідає деяке значення параметра с. Оскільки умова задачі вимагає, щоб с було найменшим, то з чотирьох кіл треба вибрати те, абсциса центра якого приймає найменше значення. Очевидно це буде коло з центром в точці О  .
.

Рис.1.1.18
Маємо  . З
. З 
 . Звідси
. Звідси  . Тоді з
. Тоді з 
 . Таким чином,
. Таким чином,  . Оскільки положенню центра О
. Оскільки положенню центра О  відповідає
відповідає  , то знаходимо
, то знаходимо 
Відповідь: 
9. При яких а множиною розв’язків нерівності  є відрізок довжиною
є відрізок довжиною  ?
?
Розв’язання. Графіком функції  є півколо з радіусом, рівним 1, яке "пливе" своїм центром по вісі абсцис. Дана нерівність буде мати Розв’язання тоді, коли точки півкола будуть вище відповідних точок прямої
є півколо з радіусом, рівним 1, яке "пливе" своїм центром по вісі абсцис. Дана нерівність буде мати Розв’язання тоді, коли точки півкола будуть вище відповідних точок прямої  . На рис.1.1.19 показано одно з можливих положень півкола.
. На рис.1.1.19 показано одно з можливих положень півкола.

Рис.1.1.19
Для цього випадку розв’язком початкової нерівності буде відрізок  . Умова вимагає, щоб
. Умова вимагає, щоб  .
.
Якщо центр О1 співпадає з точкою A (-1; 0) або розташований ліворуч, то розв’язком нерівності буде відрізок довжиною 2. Разом з тим, якщо О  співпадає з точкою O (0; 0) або знаходиться праворуч, то розв’язком нерівності буде відрізок довжиною менше, ніж
співпадає з точкою O (0; 0) або знаходиться праворуч, то розв’язком нерівності буде відрізок довжиною менше, ніж  , або взагалі розв’язків не буде. Дійсно, якщо О1 співпадає зО, то
, або взагалі розв’язків не буде. Дійсно, якщо О1 співпадає зО, то  , a x
, a x  - корінь рівняння
- корінь рівняння  Звідси
Звідси  та
та  . Таким чином, потрібне положення центра О
. Таким чином, потрібне положення центра О  визначається умовою
визначається умовою  , тобто
, тобто  .
.
Знайдемо значення x  та x
та x  . Очевидно x
. Очевидно x  - найменший корінь рівняння
- найменший корінь рівняння
 . Звідси
. Звідси  . В той же час х
. В той же час х  - корінь рівняння
- корінь рівняння  Це рівняння рівносильне системі
Це рівняння рівносильне системі

Знайдене рівняння при  має тільки один невід’ємний корінь, тобто.
має тільки один невід’ємний корінь, тобто. 
За умовою  . Розв’язав це рівняння, знаходимо
. Розв’язав це рівняння, знаходимо  ,
,  . Оскільки
. Оскільки  , то
, то  .
.
Відповідь:  .
.
10. Знайти всі значення параметра а, при яких рівняння  має єдиний розв’язок.
має єдиний розв’язок.
Розв’язання. Представимо рівняння у вигляді  . Права частина цього рівняння задає нерухомий "кут", ліва - "кут", вершина якого рухається по вісі абсцис (рис.1.1.20).
. Права частина цього рівняння задає нерухомий "кут", ліва - "кут", вершина якого рухається по вісі абсцис (рис.1.1.20).

Рис.1.1.20
Рівняння буде мати єдиний розв’язок, якщо вершина рухомого "кута"
потрапить або в точку А або в точку В.
Маємо А ( -4; 0), В ( -2; 0), і координати цих точок задовольняють рівнянню  . Тоді
. Тоді  або
або  . Звідси
. Звідси  або
або  .
.
Відповідь:  або
або  .
.
11. Знайти всі значення параметра а, для яких найменше значення функції  більше 2.
більше 2.
Розв’язання. Дана функція не задає сім’ю "кутів". За умовою задачі необхідно шукати значення параметра, при яких нерівність  виконується при будь-яких х. Це і є формулювання, рівносильна даній.
виконується при будь-яких х. Це і є формулювання, рівносильна даній.
Одержану нерівність слід переписати так:  .
.
"Кут"  повинен бути розташований так, щоб на параболі
повинен бути розташований так, щоб на параболі  не знайшлося ні однієї точки, яка б лежала вище відповідних точок "кута" або на самому "куті". Для цього вершина "кута" не повинна належати відрізку
не знайшлося ні однієї точки, яка б лежала вище відповідних точок "кута" або на самому "куті". Для цього вершина "кута" не повинна належати відрізку  (рис.1.1.21).
(рис.1.1.21).

Рис.1.1.21
Абсциси а 1 и а 2 відповідають моменту дотику. Таким чином, шукані значення параметра визначаються сукупністю нерівностей  або
або  . Залишилось знайти
. Залишилось знайти  та
та  . Значення
. Значення  та
та  знайдемо, вимагаючи відповідно від рівнянь
знайдемо, вимагаючи відповідно від рівнянь 
 мати
мати
єдиний корінь. Звідси 
 .
.
Відповідь:  або
або  .
.
12. При яких а множиною розв’язків нерівності  є відрізок числової прямої?
є відрізок числової прямої?
Розв’язання. Маємо  . Права частина цієї нерівності задає сім’ю "кутів", вершини яких лежать на прямій у = 3 (рис.1.1.22).
. Права частина цієї нерівності задає сім’ю "кутів", вершини яких лежать на прямій у = 3 (рис.1.1.22).

Рис.1.1.22
Якщо вершина "кута" знаходиться між точками А та В, то обов’язково знайдуться проміжки області визначення, на яких графік лівої частини нерівності не вище графіка правої частини. На рис.1.1.22 показано одно з проміжних положень "кута" з вершиною С. В цьому випадку розв’язком початкової нерівності будуть всі точки відрізку MN.
При  вершина "кута" знаходиться між точками А та В, і виникає бажання вважати проміжок (-8;
вершина "кута" знаходиться між точками А та В, і виникає бажання вважати проміжок (-8;
4) шуканою відповіддю. Але умова задачі вимагає, щоб розв’язком нерівності був відрізок числової прямої. А якщо вершина "кута" співпадає з будь-якою з точок відрізка EF, включаючи Е і не включаючи F (рис.1.1.23, точка F відповідає моменту дотику), то розв’язком нерівності буде або відрізок і точка, або два відрізки. Визначив координати точок Е та F, знаходимо  .
.

Рис.1.1.23
Відповідь:  .
.
Поворот
В цьому параграфі вибір сім’ї кривих не є різноманітним, а точніше він одноваріантний: члени сім’ї кривих  - прямі. Більш того, центр повороту належить прямій. Іншими словами, ми обмежимося сім’єю виду
- прямі. Більш того, центр повороту належить прямій. Іншими словами, ми обмежимося сім’єю виду  , де
, де  - центр повороту.
- центр повороту.
Такий вибір обумовлено тим, що в рівності  складно побачити аналітичне задання повороту кривих, які відрізняються від прямих. Тому про поворот, як про метод, доцільно говорити лише для прямих вказаного типа.
складно побачити аналітичне задання повороту кривих, які відрізняються від прямих. Тому про поворот, як про метод, доцільно говорити лише для прямих вказаного типа.
1. При яких  рівняння
рівняння  має три розв’язки?
має три розв’язки?
Розв’язання. Побудуємо графіки функцій  та
та  . Прямі
. Прямі  переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).
переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).

Рис.1.2.1
Рівняння буде мати три розв’язки, коли пряма  перетинає параболу в двох точках і дотикається до вершини, тобто коли
перетинає параболу в двох точках і дотикається до вершини, тобто коли  .
.









Обираємо  , так як при
, так як при  пряма дотикається вітки гіперболи нижче вісі абсцис.
пряма дотикається вітки гіперболи нижче вісі абсцис.
Відповідь: 
2. Розв’язати рівняння  і визначити значення
і визначити значення  , при яких воно має єдиний розв’язок.
, при яких воно має єдиний розв’язок.
Розв’язання. Побудуємо графіки функцій  та
та  . Прямі
. Прямі  переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).
переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).

Рис.1.2.2
Якщо  , то
, то  , звідки
, звідки 
Якщо  , то
, то  , звідки
, звідки 
Знайдемо параметр  :
:  , звідки
, звідки  , тобто
, тобто  .
.
 , звідки
, звідки  , тобто
, тобто  та
та  .
.
Відповідь: при 
 ; при
; при 
 або
або  ; при
; при  або
або 
 .
.
3. При яких значеннях  рівняння
рівняння  має одно, два, три чотири розв’язки?
має одно, два, три чотири розв’язки?
Розв’язання. Побудуємо графіки функцій  та
та  . Прямі
. Прямі  переходять друг в друга шляхом перетворення повороту з центром в точці О (9; 0).
переходять друг в друга шляхом перетворення повороту з центром в точці О (9; 0).

Рис.1.2.3
З рисунка видно, що при  рівняння має 1 розв’язок, при
рівняння має 1 розв’язок, при  - 2 розв’язки, при
- 2 розв’язки, при  - 3 розв’язки, при
- 3 розв’язки, при  - 4 розв’язки, при
- 4 розв’язки, при  - 2 розв’язки, при
- 2 розв’язки, при  - 1 розв’язок.
- 1 розв’язок.
Відповідь: при  - 1 розв’язок, при
- 1 розв’язок, при  - 2 розв’язки, при
- 2 розв’язки, при  - 3 розв’язки, при
- 3 розв’язки, при  - 4 розв’язки, при
- 4 розв’язки, при  - 2 розв’язки, при
- 2 розв’язки, при  - 1 розв’язок.
- 1 розв’язок.
4. При яких значеннях  рівняння
рівняння  має рівно 1 розв’язок? Знайти його.
має рівно 1 розв’язок? Знайти його.
Розв’язання. Запишемо ОДЗ рівняння: 
Побудуємо графіки функцій  та
та  враховуючи ОДЗ.
враховуючи ОДЗ.
Прямі  переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).
переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).

Рис.1.2.4
Рівняння можна переписати у вигляді:
 2020-01-14
2020-01-14 271
271







