2020-01-14
100
Как уже отмечалось, все алгебры считаются принадлежащими некоторому фиксированному мальцевскому многообразию и используются стандартные обозначения и определения из[1].
Напомним, что для 
и 
– конгруэнции на алгебре 
– говорят, что 
централизует (записывается: 
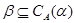), если на существует такая конгруэнция 
, что:
1) из 
всегда следует
2) для любого элемента 
всегда выполняется
3) если 
, то
Очевидно, что для любой конгруэнции 
на алгебре конгруэнция 
централизует . В этом случае 
.
Заметим, что если и – конгруэнции на группе 
и 
, то для нормальных подгрупп 
и 
группы 
и любых элементов 
, 
имеют место следующие соотношения:
Тогда
и в силу транзитивности 
из этих соотношений следует, что
По определению 2.1 получаем, что
Следующее определение центральности принадлежит Смиту.
Определение 3.1. 
, если существует такая 
, что для любого 
,
Докажем, что определение 2.1. эквивалентно определению 3.1. 
означает условие 1) из определения 2.1. И наоборот, условие 1) означает, что 
.
|
|
|
Пусть и 
– конгруэнции, удовлетворяющие определению 2.1. Из условия 2) следует, что для любого элемента 
,
Докажем обратное включение.
Пусть 
. Так как 
, то из условия 2) следует, что
В силу транзитивности имеем
и, значит, в силу условия 3) 
. Итак
Покажем, что из определения 3.1. следуют условия 2) и 3) определения 2.1. Если 
, то
Это означает 
.
Для 
получаем, что
откуда 
.
Согласно работе
Определение 3.2. Алгебра 
называется нильпотентной, если существует такой ряд конгруэнции
называемый центральным, что
Лемма 3.1. Любая подалгебра нильпотентной алгебры нильпотентна.
Доказательство:
Пусть 
– подалгебра нильпотентной алгебры . Так как обладает центральным рядом
то для любого 
на алгебре 
существует конгруэнция 
удовлетворяющая определению 2.1. А именно, из
всегда следует
и
1) для любого элемента
всегда выполняется
2) если
и
то
Заметим, что в дальнейшем, для сокращения записи, будем учитывать тот факт, что
тогда и только тогда, когда
Построим следующий ряд конгруэнции на алгебре :
где
Покажем, что этот ряд является центральным. Для этого на алгебре 
для любого 
определим бинарное отношение 
следующим образом:
тогда и только тогда, когда
Покажем, что 
– конгруэнция на алгебре 
. Пусть
Тогда
и для любой 
-арной операции 
имеем
|
|
|
Следовательно,
Итак, – подалгебра алгебры 
.
Очевидно, что для любого элемента 
имеет место
Таким образом, согласно лемме 2.3, – конгруэнция на алгебре .
Пусть
Тогда 
и так как 
, то
Если 
, то 
и, значит,
т.е.
Пусть, наконец,
Тогда
и так как
Следовательно,
Итак, конгруэнция удовлетворяет определению 2.1. для любого 
. Лемма доказана.
Лемма 3.2. Пусть и – конгруэнции на алгебре ,
и 
– изоморфизм, определенный на алгебре .
Тогда для любого элемента 
отображение
определяет изоморфизм алгебры 
на алгебру 
, при котором
Доказательство:
Очевидно, что 
– изоморфизм алгебры на алгебру 
, при котором конгруэнции 
и изоморфны соответственно конгруэнциям 
и 
.
Так как 
, то существует конгруэнция 
на алгебре 
, удовлетворяющая определению 2.1. Изоморфизм 
алебры на алгебру 
индуцирует в свою очередь изоморфизм 
алгебры 
на алгебру 
такой, что
для любых элементов 
, 
.
Но тогда легко проверить, что 
– конгруэнция на алгебре 
изоморфная конгруэнции 
. Это и означает, что
Лемма доказана.
Лемма 3.3. Фактор-алгебра нильпотентной алгебры нильпотентна.
Доказательство:
Пусть
центральный ряд алгебры . Покажем, что для любой конгруэнции 
на алгебре ряд
является центральным, т.е.
для любого . В силу известных теорем об изоморфизмах для алгебр (см., например, теоремы II.3.7, II.3.11) и леммы 3.2., достаточно показать, что
Пусть 
– конгруэнция на алгебре 
, удовлетворяющая определению 2.1. Определим бинарное отношение на алгебре 
следующим образом
тогда и только тогда, когда найдутся такие элементы 
, что
и
Непосредственной проверкой убеждаемся, что – конгруэнция на алгебре .
Таким образом осталось показать, что удовлетворяет определению 2.1.
Пусть
тогда из соотношения
следует, что
Так как
то 
. Итак,
Пусть . Тогда для некоторого элемента 
, 
и 
.
Таким образом,
следовательно,
Так как 
, то это означает, что
Пусть
где
Покажем, что 
. В силу определения 
найдутся 
, что
и
При этом имеют место следующие соотношения:
Следовательно,
Но тогда по определению 3.2.
А так как 
, то
Теперь из того, что
следует, что
Лемма доказана.
Доказательство следующего результата осуществляется простой проверкой.
Лемма 3.4. Пусть 
– конгруэнция на алгебре 
, 
. Пологая
тогда и только тогда, когда 
для любого 
, получаем конгруэнцию на алгебре 
.
Лемма 3.5. Прямое произведение конечного числа нильпотентных алгебр нильпотентно.
Доказательство:
Очевидно, достаточно показать, что если 
, 
и 
– нильпотентные алгебры, то 
– нильпотентная алгебра.
Пусть
центральные ряды алгебр и соответственно. Если 
, то, уплотнив первый ряд повторяющимися членами, получим центральный ряд алгебры длины 
. Таким образом, можно считать, что эти ряды имеют одинаковую длину, равную 
.
Построим теперь ряд конгруэнции на алгебре следующим образом:
где 
тогда и только тогда, когда 
, 
, 
.
Покажем, что последний ряд является центральным, т.е. 
для произвольного . Так как
то на алгебрах 
и 
соответственно заданы конгруэнци 
и 
, удовлетворяющие определению 2.1.
Определим бинарное отношение 
на алгебре 
следующим образом:
и только тогда, когда
и
Легко непосредственной проверкой убедиться, что 
– конгруэнция на алгебре . Осталось показать, что 
удовлетворяет определению 2.1.
|
|
|
Пусть имеет место
Тогда согласно введенному определению
и
откуда следует, что
т.е.
Пусть
Это означает
Но тогда
и
Следовательно,
Пусть имеет место
Это означает, что
и
Значит, 
и 
, т.е. 
. Лемма, доказана.
Как известно, наследственной формацией называется класс алгебр, замкнутых относительно фактор-алгебр, подпрямых произведений и относительно подалгебр.
Результаты, полученные в леммах 3.1, 3.3, 3.5 можно сформулировать в виде следующей теоремы.
Теорема 7 Класс всех нильпотентных алгебр мальцевского многообразия является наследственной формацией.
Определение 3.3. 
-арная группа 
называется нильпотентной, если она обладает таким нормальным рядом
что
и
для любого 
.
Так как конгруэнции на 
-арных группах попарно перестановочны (смотри, например,), то это дает возможность использовать полученные результаты в исследовании таких групп.
Лемма 3.6. Пусть – 
-арная группа. и – нормальные подгруппы группы 
и 
.
Тогда 
, где 
и конгруэнции, индуцированные соответственно подгруппами и на группе .
Доказательство:
Подгруппы и индуцируют на группе 
конгруэнции и 
, определяемые следующим образом:
– -арная операция.
Определим на бинарное отношение 
следующим образом:
тогда и только тогда, когда существуют такие последовательности элементов 
и 
из и соответственно, что
Покажем, что 
– подалгебра алгебры 
. Для сокращения записи будем в дальнейшем опускать 
-арный оператор 
.
Пусть
Так как 
, то
Так как 
, то
Поэтому в силу того, что 
,
Итак, 
– подалгебра алгебры .
Пусть – нейтральная последовательность группы , а, следовательно, и группы 
. Тогда из определения бинарного отношения 
следует, что
|
|
|
Тем самым доказало, что 
– конгруэнция на .
Тo, что удовлетворяет определению 2.1, очевидно. Лемма доказана.
Лемма 3.7. Пусть 
– нильпотентная 
-арная группа. Тогда 
удовлетворяет определению 2.1.
Доказательство:
Так как 
для любого , то 
индуцирует конгруэнцию 
на 
. Таким образом 
обладает рядом конгруэнции, который в силу леммы 3.6 будет являться центральным. Лемма доказана.
В частности, для произвольной бинарной группы отсюда следует, что нильпотентна тогда и только тогда, когда, удовлетворяет определению 3.2. В этом случае теорема 3.2 просто констатируе тот факт, что класс всех нильпотентных групп образует наследственную формацию.
