Геометрические приложения определенного интеграла

 

Вычисление площадей плоских фигур

 

Вычисление площади в декартовой системе координат.

Если на отрезке 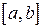 непрерывная функция , то определенный интеграл на этом отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции , т.е.  (см. рис. 4).

Рис.4.

Если график расположен ниже оси Ох, т.е. <0, то  и для площади можно записать: (см. рис. 5).

Рис. 5.

Объединяя обе формулы, получим: .

Пример. Найти площадь фигуры, ограниченной линиями .

Рис. 6

    Искомая площадь (заштрихована на рисунке 6) может быть найдена по формуле:

 (кв.ед).

 

Вычисление площади в случае, когда кривая задана параметрическими уравнениями

Пусть кривая  задана параметрическими уравнениями

 , где , и .

Построив кривую в декартовой системе координат для вычисления площади запишем формулу

= .

 

Вычисление площади в полярной системе координат

Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид , где r - длина радиус–вектора, соединяющего полюс с произвольной точкой кривой, а j - угол наклона этого радиус–вектора к полярной оси (см. рис.7).

Рис. 7.

    Площадь криволинейного сектора может быть найдена по формуле

Пример. Найти площадь круга, ограниченного окружностью  (см. рис.8).

Рис.8.

.