Вычисление криволинейного интеграла первого рода.
Пусть гладкая кривая  задана параметрически уравнениями
задана параметрически уравнениями  . При этом для определенности будем считать, что точке
. При этом для определенности будем считать, что точке  соответствует значение
соответствует значение  , точке
, точке  . Тогда для любой точки
. Тогда для любой точки  кривой
кривой  длина
длина  дуги
дуги  может быть вычислена по формуле
может быть вычислена по формуле
 (6)
(6)
откуда находим
 (7)
(7)
Тогда в правом интеграле равенства (3), сделав замену  и учитывая (7), получим
и учитывая (7), получим
 (8)
(8)
Отметим некоторые свойства криволинейного интеграла первого рода.
1. Свойство линейности. Если существуют криволинейные интегралы первого рода  и
и  , то для любых действительных чисел
, то для любых действительных чисел  существует интеграл
существует интеграл  , и при этом справедливо равенство
, и при этом справедливо равенство
 .
.
2. Свойство аддитивности. Если существует интеграл  , то для любой точки
, то для любой точки 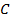 кривой
кривой  существуют интегралы
существуют интегралы  и
и  , при этом справедливо равенство
, при этом справедливо равенство
 .
.
Физический смысл криволинейного интеграла первого рода.
Пусть на плоскости  дана некоторая кусочно гладкая кривая
дана некоторая кусочно гладкая кривая  , вдоль которой расположены массы. Пусть
, вдоль которой расположены массы. Пусть  линейная плотность массы в точке
линейная плотность массы в точке  кривой
кривой  . Разбивая кривую
. Разбивая кривую  точками
точками  и считая, что в каждой точке частичной дуги
и считая, что в каждой точке частичной дуги  плотность
плотность  приблизительно равна одному и тому же значению
приблизительно равна одному и тому же значению  , найдем массу дуги
, найдем массу дуги  . Эта масса равна
. Эта масса равна  , тогда масса всей кривой будет приблизительно равна
, тогда масса всей кривой будет приблизительно равна
|
|
|
 .
.
Переходя к пределу в последнем равенстве, при стремлении к нулю наибольшей длины  частичных дуг, получим
частичных дуг, получим
 .
.
Таким образом, криволинейный интеграл  определяет массу кривой
определяет массу кривой  , имеющей в каждой точке
, имеющей в каждой точке  линейную плотность массы
линейную плотность массы  .
.
3. Криволинейный интеграл первого рода для случая пространственной кривой.
Пусть  – гладкая или кусочно гладкая кривая в пространстве
– гладкая или кусочно гладкая кривая в пространстве  , и пусть в каждой точке кривой
, и пусть в каждой точке кривой  определена некоторая функция
определена некоторая функция  .
.
Рассмотрим произвольное разбиение кривой  . Выбирая в каждой частичной дуге
. Выбирая в каждой частичной дуге  произвольную точку
произвольную точку  , составим интегральную сумму
, составим интегральную сумму
 (9)
(9)
где  - длина
- длина  ой частичной дуги
ой частичной дуги  .
.
Определение. Если существует предел  интегральной суммы (9) при стремлении к нулю наибольшей длины
интегральной суммы (9) при стремлении к нулю наибольшей длины  частичных дуг, то этот предел называется криволинейным интегралом первого рода от функции
частичных дуг, то этот предел называется криволинейным интегралом первого рода от функции  по кривой
по кривой  и обозначается символом
и обозначается символом  либо
либо  .
.
Точно так же, как для плоской кривой, доказывается, что если кривая  задана параметрически уравнениями
задана параметрически уравнениями  , то справедливо равенство
, то справедливо равенство
 (10)
(10)
§3.Криволинейные интегралы второго рода
Пусть на кривой  плоскости
плоскости  заданы две ограниченные функции
заданы две ограниченные функции  . Разобьем кривую
. Разобьем кривую  на
на  частей точками
частей точками  . В каждой частичной дуге
. В каждой частичной дуге  выберем произвольную точку
выберем произвольную точку  и вычислим в ней значения функций
и вычислим в ней значения функций  и
и  . Значение
. Значение  мы домножим на этот раз не на длину дуги
мы домножим на этот раз не на длину дуги  , а на величину проекции дуги на ось
, а на величину проекции дуги на ось  , т.е. на
, т.е. на  ; и составим сумму
; и составим сумму
|
|
|
 (1)
(1)
Аналогично, значение  умножим на проекцию дуги
умножим на проекцию дуги  на ось
на ось  и составим сумму
и составим сумму
 (2)
(2)
Как и раньше, через  будем обозначать максимальную длину частичных дуг.
будем обозначать максимальную длину частичных дуг.
Определение. Если существует предел интегральной суммы (1) при стремлении к нулю максимальной длины  частичных дуг
частичных дуг  , то этот предел называется криволинейным интегралом второго рода по кривой
, то этот предел называется криволинейным интегралом второго рода по кривой  взятой от функции
взятой от функции 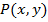 и обозначается следующим образом
и обозначается следующим образом  .
.
Если существует предел интегральной суммы (2) при  , то этот предел также называется криволинейным интегралом второго род а и обозначается следующим образом
, то этот предел также называется криволинейным интегралом второго род а и обозначается следующим образом  .
.
Сумма  называется общим криволинейным интегралом второго рода и обозначается символом
называется общим криволинейным интегралом второго рода и обозначается символом  .
.
Рассмотрим теперь случай пространственной кривой.
Пусть на кривой  пространства
пространства  определены ограниченные функции
определены ограниченные функции  ,
,  и
и  . Рассмотрим произвольное разбиение кривой
. Рассмотрим произвольное разбиение кривой  точками
точками  . Взяв на каждой частичной дуге
. Взяв на каждой частичной дуге  произвольно по точке
произвольно по точке  , составим следующие интегральные суммы
, составим следующие интегральные суммы
 (3)
(3)
 (4)
(4)
 (5)
(5)
где  - величина проекции дуги
- величина проекции дуги  на ось
на ось  ,
,  - величина проекции дуги
- величина проекции дуги  на ось
на ось  ,
,  - величина проекции дуги
- величина проекции дуги  на ось
на ось  .
.
Определение. Если существуют пределы интегральных сумм (3), (4), (5) при стремлении к нулю максимальной длины  частичных дуг, то эти пределы называются криволинейными интегралами второго рода и обозначаются соответственно символами
частичных дуг, то эти пределы называются криволинейными интегралами второго рода и обозначаются соответственно символами
 ,
,  ,
,  .
.
Сумма

называется общим криволинейным интегралом и обозначается символом  .
.
Криволинейные интегралы второго рода, как и интегралы первого рода, легко сводятся к определенным интегралам.
Рассмотрим случай плоской кривой. Пусть кривая  задана параметрически уравнениями
задана параметрически уравнениями  , где
, где  и их производные
и их производные  непрерывные функции, причем точке
непрерывные функции, причем точке  кривой соответствует значении
кривой соответствует значении  , точке
, точке  значение
значение  . Кроме того будем предполагать, что
. Кроме того будем предполагать, что
 .
.
Пусть функции 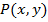 и
и 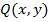 непрерывны вдоль прямой
непрерывны вдоль прямой  . Тогда справедливы следующие равенства:
. Тогда справедливы следующие равенства:
 , (6)
, (6)
 , (7)
, (7)
 (8)
(8)
Доказательство равенств (6), (7), (8) мы не приводим.
Отметим, что если кривая  в пространстве
в пространстве  задана параметрически
задана параметрически  ,
,  ,
,  ,
,  , где функции
, где функции  и их производные
и их производные  непрерывны, причем
непрерывны, причем  , точке
, точке  соответствует значение
соответствует значение  , а точке
, а точке  -
-  , а функции
, а функции  непрерывны вдоль кривой
непрерывны вдоль кривой  , то справедливы следующие равенства
, то справедливы следующие равенства
 , (9)
, (9)
 , (10)
, (10)
 , (11)
, (11)

 , (12)
, (12)
Из формул (6), (7), (8) следует, что криволинейный интеграл второго рода обладает свойствами, аналогичными свойствам определенного интеграла.
В отличие от криволинейного интеграла первого рода криволинейный интеграл второго рода зависит от того, в каком направлении проходится кривая  , и меняет знак при изменении направления обхода, то есть
, и меняет знак при изменении направления обхода, то есть
 ,
, 
Действительно, при изменении направления обхода кривой, в интегральных суммах (1) и (2) поменяются знаки проекций  и
и  , следовательно, сами интегральные суммы и их пределы изменят знак.
, следовательно, сами интегральные суммы и их пределы изменят знак.
Пусть теперь точки  совпадают, то есть кривая
совпадают, то есть кривая  является замкнутой кривой. В этом случае из двух возможных направлений обхода замкнутой кривой
является замкнутой кривой. В этом случае из двух возможных направлений обхода замкнутой кривой  , положительным будем называть то направление, при котором область, лежащая внутри кривой
, положительным будем называть то направление, при котором область, лежащая внутри кривой  , остается слева по отношению к точке, совершающей обход. Противоположное направление обхода будем называть отрицательным.
, остается слева по отношению к точке, совершающей обход. Противоположное направление обхода будем называть отрицательным.
Криволинейный интеграл по замкнутому контуру  , пробегаемому в положительном направлении, будем обозначать символом
, пробегаемому в положительном направлении, будем обозначать символом
|
|
|

Формула Грина
Пусть 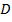 – произвольная замкнутая, ограниченная область на плоскости
– произвольная замкнутая, ограниченная область на плоскости  . Будем предполагать, что граница области
. Будем предполагать, что граница области  гладкая или кусочно-гладкая кривая
гладкая или кусочно-гладкая кривая  . Кроме этого предположим, что любая прямая, параллельная
. Кроме этого предположим, что любая прямая, параллельная  или
или  , пересекает границу области
, пересекает границу области 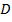 не менее чем в двух точках. Такие области будет называть простыми.
не менее чем в двух точках. Такие области будет называть простыми.
Выберем на кривой  , являющейся границей области
, являющейся границей области 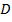 , такое направление, что при обходе области
, такое направление, что при обходе области 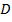 по кривой
по кривой  область
область 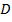 остается слева.
остается слева.

(рис. 3.1)
Такое направление будем называть положительным. Противоположное направление обхода кривой  будем называть отрицательным.
будем называть отрицательным.
Для обозначения криволинейного интеграла по замкнутой кривой  , пробегаемой в положительном направлении, будем пользоваться символом
, пробегаемой в положительном направлении, будем пользоваться символом

Теорема 5. 1.
Пусть функции 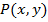 ,
, 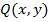 и их частичные производные
и их частичные производные 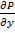 и
и 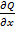 непрерывны в простой замкнутой области
непрерывны в простой замкнутой области 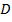 , ограниченной кусочно-гладкой кривой
, ограниченной кусочно-гладкой кривой  ,
,
 (13)
(13)
Формула (13) называется формулой Грина. Эта формула устанавливает связь между криволинейным интегралом второго рода по замкнутой кривой  и двойным интегралом по области – ограниченной кривой
и двойным интегралом по области – ограниченной кривой  .
.
Доказательство: Предположим, что кривую  можно задать как уравнениями
можно задать как уравнениями  , так и уравнениями
, так и уравнениями  .
.
Рассмотрим двойной интеграл  .
.

(рис. 3.2)
Применяя теорему 1. 5. Сведем этот двойной интеграл к повторному
 (14)
(14)
В силу равенств (6) и (7), каждый из двух определенных интегралов в равенстве соответственно равен
 (15)
(15)
 (16)
(16)
Таким образом,
 (17)
(17)
Рассматривая теперь границу области 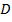 как объединение двух графиков
как объединение двух графиков  , и повторяя рассуждения, приведенные выше, мы получим равенство
, и повторяя рассуждения, приведенные выше, мы получим равенство
 (18)
(18)
Вычитая из равенства (17) равенство (18), найдем

Тем самым справедливость формулы Грина доказана.
Геометрические приложения криволинейного интеграла второго рода.
Пусть  – некоторая область, а
– некоторая область, а  – ее граница
– ее граница  . Предположим, что
. Предположим, что  – гладкая или кусочно-гладкая кривая.
– гладкая или кусочно-гладкая кривая.
|
|
|
Пусть  и
и  – произвольные функции такие, что
– произвольные функции такие, что  .
.
Тогда по формуле Грина
 (19)
(19)
Возьмем в качестве функции  , а в качестве
, а в качестве  , тогда
, тогда  ,
,  , и из формулы (19) получим
, и из формулы (19) получим
 (20)
(20)
Так как  , где
, где  – площадь области
– площадь области 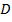 , то
, то
 (21)
(21)
Пусть теперь  а
а  , тогда
, тогда  ,
,  , поэтому из формулы (19) получим
, поэтому из формулы (19) получим
 (22)
(22)
Складывая равенства (21) и (22), а затем, поделив обе части полученного при этом равенства, найдем
 (23)
(23)
Итак, мы получили три формулы для вычисления площадей плоских фигур, ограниченных кривой  .
.
Пример:
Найти площадь фигуры, ограниченной эллипсом

Запишем параметрические уравнения эллипса  ,
,  .
.
Тогда  , и по формуле (22) найдем
, и по формуле (22) найдем

 2020-04-12
2020-04-12 1378
1378