Квант. 08.01.04. Поведение функции в окрестности полюса (Т)

Рассмотрим однозначную аналитическую функцию

Пусть 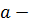 ее полюс 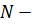го порядка

Тогда

Доказательство.

Пусть 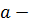полюс 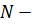го порядка, то есть разложение Лорана имеет вид

Обозначим правильную часть , а главную

 

Имеем

То есть предел функции в полюсе равен бесконечности. Найдем теперь предел произведения

 

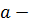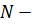Получили конечный предел. Таким образом, если полюс го порядка, то

Замечание.

Верно и обратное утверждение. Сначала установим связь между нулем и полюсом.

Квант. 08.01.05. Определение нуля аналитической функции (О)

Рассмотрим аналитическую функцию  

Пусть выполняются условия

 

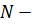Тогда точка  называется нулем го порядка функции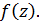

 

Квант. 08.01.06. Свойство нуля аналитической функции (Св)

Рассмотрим аналитическую функцию  

Пусть точка  является ее нулем 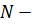го порядка

Тогда для этого необходимо и достаточно, чтобы функция представлялась в виде

 

где аналитическая функция.

Доказательство.

     Разложение в ряд Тейлора в окрестности точки  имеет вид

Обозначим

Эта функция аналитическая в точке  как сумма степенного ряда и  . Таким образом, в окрестности нуля 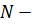го порядка аналитическая функция представляется в виде

где аналитическая функция. Верно и обратное: если  представляется в виде (1), то точка  является для нее нулем 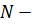го порядка, что легко проверить.

Квант. 08.01.07. Связь между нулем и полюсом (Т)

Рассмотрим аналитическую функцию  

Пусть точка  является ее полюсом (нулем) 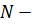го порядка

Тогда для функции  точка  является нулем (полюсом) 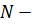го порядка.

Доказательство.
 а) Пусть 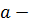полюс 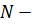го порядка для функции ,

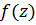аналитическая функция,

 

где аналитическая функция,  То есть 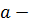нуль порядка  для функции  

б) Пусть тепер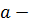ь нуль 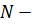го порядка для функции ,

 

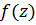где аналитическая функция,  Тогда

и точка  является полюсом 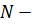го порядка. Теорема доказана.